Réalisation de stratégies équilibrées de capitaux propres pour les positions longues à court terme avec un alignement ordonné

Réalisation de stratégies équilibrées de capitaux propres pour les positions longues à court terme avec un alignement ordonné

Dans l'article précédent (https://www.fmz.com/bbs-topic/9862), nous avons introduit des stratégies de trading en paire et démontré comment créer et automatiser des stratégies de trading en utilisant des données et des analyses mathématiques.

La stratégie équilibrée des positions longues et courtes est une extension naturelle de la stratégie de négociation de paires applicable à un panier d'objets de négociation. Elle convient particulièrement aux marchés de négociation avec de nombreuses variétés et interrelations, tels que les marchés de devises numériques et les marchés à terme des matières premières.

Principes de base

La stratégie d'équité équilibrée pour les positions longues et courtes consiste à aller long et à aller court un panier d'objectifs de trading simultanément. Tout comme le trading en paire, elle détermine quelle cible d'investissement est bon marché et quelle cible d'investissement est chère. La différence est que la stratégie d'équité équilibrée pour les positions longues et courtes disposera toutes les cibles d'investissement dans un pool de sélection d'actions pour déterminer quelles cibles d'investissement sont relativement bon marché ou chères. Ensuite, elle va long les n premières cibles d'investissement en fonction du classement et court les n dernières cibles d'investissement dans le même montant (valeur totale des positions longues = valeur totale des positions courtes).

Vous souvenez-vous de ce que nous avons dit que le trading de paires est une stratégie neutre sur le marché? La même chose est vraie pour la stratégie équilibrée des positions courtes longues, car la quantité égale de positions longues et courtes garantit que la stratégie restera neutre sur le marché (non affectée par les fluctuations du marché). La stratégie est également statistiquement robuste; en classant les objectifs d'investissement et en détenant des positions longues, vous pouvez ouvrir des positions sur votre modèle de classement plusieurs fois, pas seulement une fois.

Quel est le système de classement?

Le schéma de classement est un modèle qui peut attribuer la priorité à chaque sujet d'investissement en fonction des performances attendues. Les facteurs peuvent être des facteurs de valeur, des indicateurs techniques, des modèles de prix ou une combinaison de tous les facteurs ci-dessus. Par exemple, vous pouvez utiliser des indicateurs de dynamique pour classer une série d'objectifs d'investissement de suivi de tendance: on s'attend à ce que les objectifs d'investissement avec la plus forte dynamique continuent de bien performer et obtiennent le meilleur classement; L'objet d'investissement avec la moindre dynamique a la pire performance et les plus faibles rendements.

Le succès de cette stratégie dépend presque entièrement du système de classement utilisé, c'est-à-dire que votre système de classement peut séparer l'objectif d'investissement à haut rendement de l'objectif d'investissement à faible rendement, afin de mieux réaliser le retour de la stratégie des objectifs d'investissement de positions longues et courtes.

Comment faire un classement?

Une fois que nous avons déterminé le schéma de classement, nous espérons en tirer un profit. Nous le faisons en investissant le même montant de capital pour aller long les objectifs d'investissement supérieurs et aller court les objectifs d'investissement inférieurs. Cela garantit que la stratégie ne fera que des profits proportionnels à la qualité du classement, et elle sera "neutre sur le marché".

Supposons que vous classiez toutes les cibles d'investissement m, et que vous ayez n dollars pour investir, et que vous souhaitiez détenir un total de 2p (où m>2p) positions.

• Vous classez les objets d'investissement comme: 1,...,p position, allez court l'objectif d'investissement de 2/2p USD.

• Vous classez les objets d'investissement comme: m-p,...,m position, allez long l'objectif d'investissement de n/2p USD.

Note: Comme le prix de l'objet de l'investissement causé par la fluctuation des prix ne divisera pas toujours n/2p uniformément, et que certains objets de l'investissement doivent être achetés avec des nombres entiers, il y aura des algorithmes inexacts, qui devraient être aussi proches que possible de ce nombre.

N/2p = 100000/1000 = 100

Cela causera un gros problème pour les scores dont le prix est supérieur à 100 (comme le marché des contrats à terme sur matières premières), car vous ne pouvez pas ouvrir une position avec un prix fractionné (ce problème n'existe pas sur les marchés de devises numériques).

Prenons un exemple hypothétique.

• Construire notre environnement de recherche sur la plateforme FMZ Quant

Tout d'abord, afin de travailler en douceur, nous devons construire notre environnement de recherche.FMZ.COM) pour construire notre environnement de recherche, principalement pour utiliser l'interface API pratique et rapide et le système Docker bien emballé de cette plateforme plus tard.

Dans le nom officiel de la plateforme FMZ Quant, ce système Docker est appelé le système Docker.

Veuillez consulter mon précédent article sur le déploiement d'un docker et d'un robot:https://www.fmz.com/bbs-topic/9864.

Les lecteurs qui veulent acheter leur propre serveur de cloud computing pour déployer des dockers peuvent se référer à cet article:https://www.fmz.com/digest-topic/5711.

Après avoir déployé avec succès le serveur de cloud computing et le système docker, nous allons ensuite installer le plus grand artefact actuel de Python: Anaconda.

Afin de réaliser tous les environnements de programme pertinents (bibliothèques de dépendances, gestion de version, etc.) requis dans cet article, le moyen le plus simple est d'utiliser Anaconda.

Pour la méthode d'installation d'Anaconda, veuillez consulter le guide officiel d'Anaconda:https://www.anaconda.com/distribution/.

Cet article utilisera également numpy et pandas, deux bibliothèques populaires et importantes dans l'informatique scientifique Python.

Le travail de base ci-dessus peut également faire référence à mes articles précédents, qui présentent comment configurer l'environnement Anaconda et les bibliothèques numpy et pandas. Pour plus de détails, veuillez vous référer à:https://www.fmz.com/digest-topic/9863.

Nous générons des objectifs d'investissement aléatoires et des facteurs aléatoires pour les classer.

import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
## PROBLEM SETUP ##
# Generate stocks and a random factor value for them
stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)
# Generate future returns for these are dependent on our factor values
future_returns = current_factor_values + np.random.normal(0, 1, 10000)
# Put both the factor values and returns into one dataframe
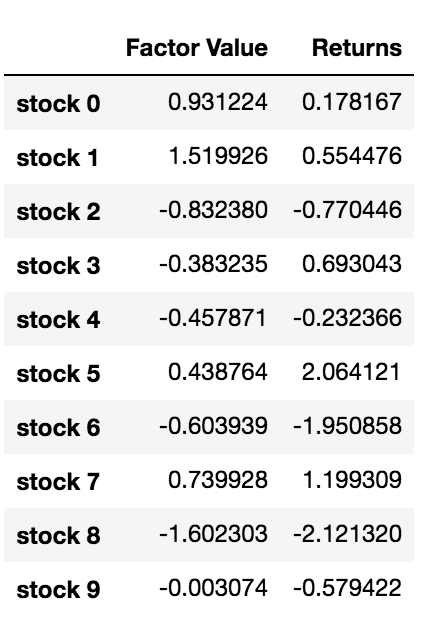
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

Maintenant que nous avons les valeurs et les rendements des facteurs, nous pouvons voir ce qui se passe si nous classons les objectifs d'investissement en fonction des valeurs des facteurs et puis ouvrir des positions longues et courtes.

# Rank stocks
ranked_data = data.sort_values('Factor Value')
# Compute the returns of each basket with a basket size 500, so total (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)
for i in range(number_of_baskets):
    start = i * 500
    end = i * 500 + 500 
    basket_returns[i] = ranked_data[start:end]['Returns'].mean()
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

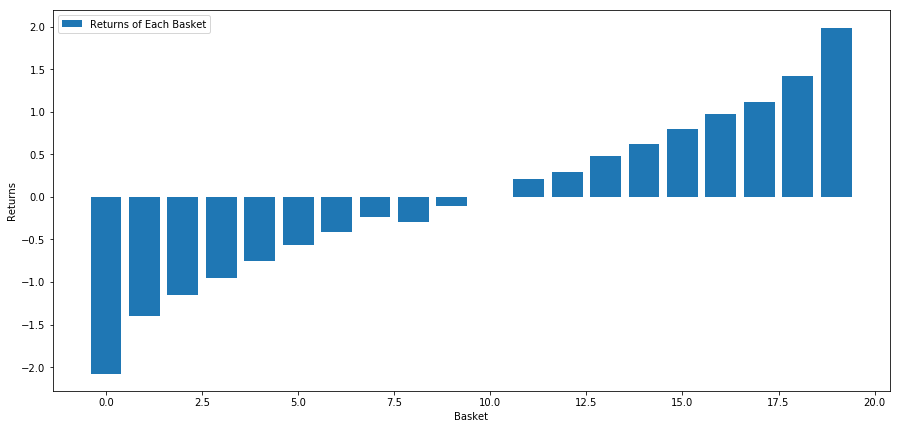
Notre stratégie est d'aller long le premier panier classé des groupes cibles d'investissement; aller court du dixième panier classé.

basket_returns[number_of_baskets-1] - basket_returns[0]

Le résultat est: 4.172

Mettez de l'argent sur notre modèle de classement afin qu'il puisse séparer les objectifs d'investissement à haut rendement des objectifs d'investissement à faible rendement.

L'avantage de l'arbitrage basé sur le classement est qu'il n'est pas affecté par le désordre du marché, mais que le désordre du marché peut être utilisé.

Considérons un exemple du monde réel.

Nous avons chargé des données pour 32 actions dans différents secteurs dans l'indice S&P 500 et avons essayé de les classer.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
                'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
                'HD','LOW','KO','LLY','MCD','MET','NEM',
                'PEP','PG','M','SWN','T','TGT',
                'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
price = 'adjClose'

Utilisons l'indicateur de dynamique normalisé pour une période d'un mois comme base de classement.

## Define normalized momentum
def momentum(dataDf, period):
    return dataDf.sub(dataDf.shift(period), fill_value=0) / dataDf.iloc[-1]
## Load relevant prices in a dataframe
data = ds.getBookDataByFeature()['Adj Close']
#Let's load momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

Maintenant, nous allons analyser le comportement de nos actions et voir comment nos actions fonctionnent sur le marché dans le facteur de classement que nous choisissons.

Analysez les données

Le comportement des stocks

Voyons comment notre panier de stocks sélectionné fonctionne dans notre modèle de classement. Pour ce faire, calculons le rendement hebdomadaire à terme pour tous les stocks. Ensuite, nous pouvons voir la corrélation entre le rendement à terme d'une semaine de chaque stock et l'élan des 30 jours précédents. Les stocks montrant une corrélation positive sont des suiveurs de tendance, tandis que les stocks montrant une corrélation négative sont des inversions moyennes.

# Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = True)
# Calculate correlations between momentum and returns
correlations = pd.DataFrame(index = returns.columns, columns = ['Scores', 'pvalues'])
mscores = mscores[mscores.index.isin(returns.index)]
for i in correlations.index:
    score, pvalue = stats.spearmanr(mscores[i], returns[i])
    correlations[‘pvalues’].loc[i] = pvalue
    correlations[‘Scores’].loc[i] = score
correlations.dropna(inplace = True)
correlations.sort_values('Scores', inplace=True)
l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations['Scores'])
plt.xlabel('Stocks')
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.legend(['Correlation over All Data'])
plt.ylabel('Correlation between %s day Momentum Scores and %s-day forward returns by Stock'%(day,forward_return_day));
plt.show()

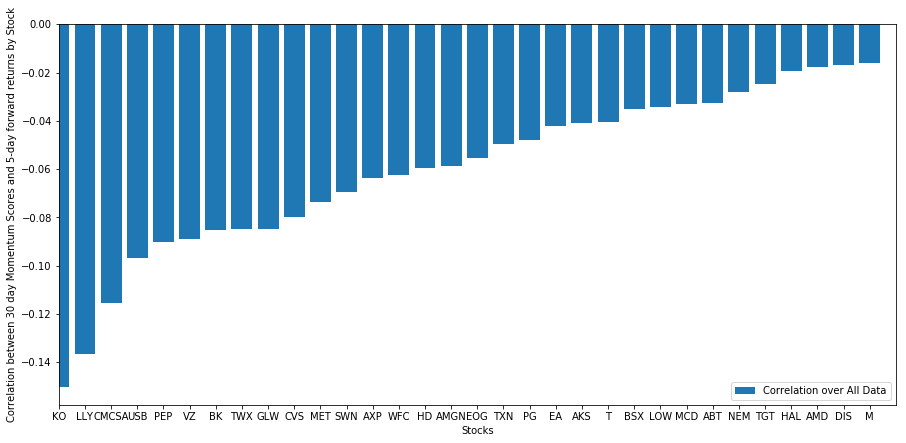
Toutes nos actions ont une réversion moyenne dans une certaine mesure! (Évidemment, l'univers que nous avons choisi fonctionne ainsi.) Cela nous dit que si les actions se classent en tête dans l'analyse de l'élan, nous devrions nous attendre à ce qu'elles se comportent mal la semaine prochaine.

Corrélation entre le classement des scores de l'analyse de l'élan et les rendements

Ensuite, nous devons voir la corrélation entre nos scores de classement et les rendements globaux à terme du marché, c'est-à-dire la relation entre le taux de rendement prévu et notre facteur de classement.

À cette fin, nous calculons la corrélation quotidienne entre la dynamique de 30 jours de toutes les actions et le rendement à terme d'une semaine.

correl_scores = pd.DataFrame(index = returns.index.intersection(mscores.index), columns = ['Scores', 'pvalues'])
for i in correl_scores.index:
    score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
    correl_scores['pvalues'].loc[i] = pvalue
    correl_scores['Scores'].loc[i] = score
correl_scores.dropna(inplace = True)
l = correl_scores.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correl_scores['Scores'])
plt.hlines(np.mean(correl_scores['Scores']), 1,l+1, colors='r', linestyles='dashed')
plt.xlabel('Day')
plt.xlim((1, l+1))
plt.legend(['Mean Correlation over All Data', 'Daily Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

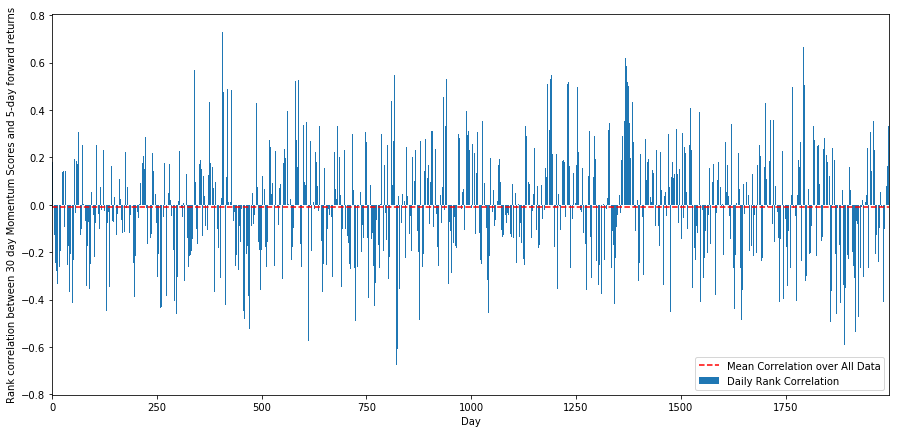
Les corrélations quotidiennes montrent une corrélation très complexe mais très légère (ce qui est attendu puisque nous avons dit que tous les stocks reviendront à la moyenne).

monthly_mean_correl =correl_scores['Scores'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colors='r', linestyles='dashed')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

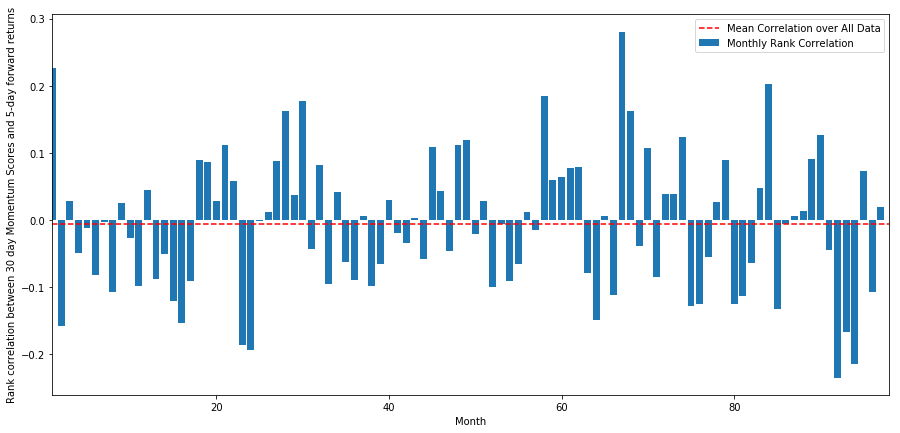
Nous pouvons voir que la corrélation moyenne est légèrement négative à nouveau, mais elle change aussi beaucoup chaque mois.

Rentabilité moyenne d'un panier d'actions

Nous avons calculé le rendement sur un panier de stocks tiré de notre classement. si nous classons tous les stocks et les divisons en nn groupes, quel est le rendement moyen de chaque groupe?

La première étape consiste à créer une fonction qui donnera le rendement moyen et le facteur de classement de chaque panier donné chaque mois.

def compute_basket_returns(factor, forward_returns, number_of_baskets, index):
data = pd.concat([factor.loc[index],forward_returns.loc[index]], axis=1)
    # Rank the equities on the factor values
    data.columns = ['Factor Value', 'Forward Returns']
    data.sort_values('Factor Value', inplace=True)
    # How many equities per basket
    equities_per_basket = np.floor(len(data.index) / number_of_baskets)
basket_returns = np.zeros(number_of_baskets)
# Compute the returns of each basket
    for i in range(number_of_baskets):
        start = i * equities_per_basket
        if i == number_of_baskets - 1:
            # Handle having a few extra in the last basket when our number of equities doesn't divide well
            end = len(data.index) - 1
        else:
            end = i * equities_per_basket + equities_per_basket
        # Actually compute the mean returns for each basket
        #s = data.index.iloc[start]
        #e = data.index.iloc[end]
        basket_returns[i] = data.iloc[int(start):int(end)]['Forward Returns'].mean()
        
    return basket_returns

Lorsque nous classons les actions en fonction de ce score, nous calculons le rendement moyen de chaque panier. Cela devrait nous permettre de comprendre leur relation pendant longtemps.

number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(float).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = True)
for m in forward_returns.index.intersection(resampled_scores.index):
    basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
    mean_basket_returns += basket_returns
mean_basket_returns /= l    
print(mean_basket_returns)
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

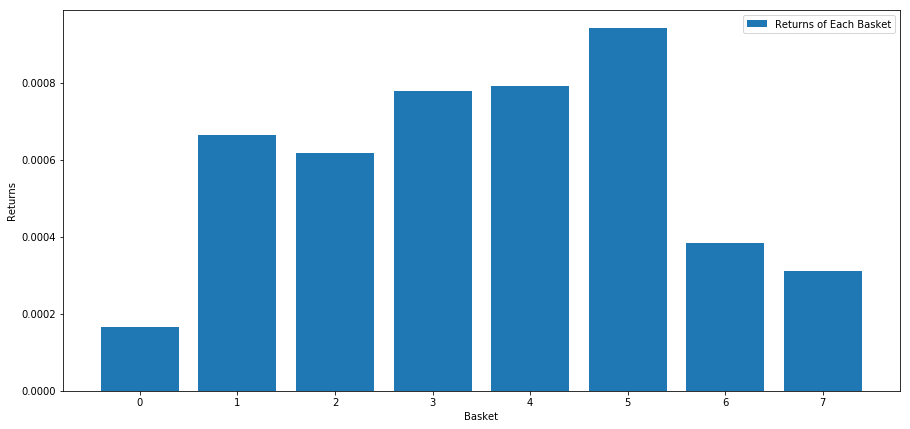
Il semble que nous puissions séparer les personnes performantes des moins performantes.

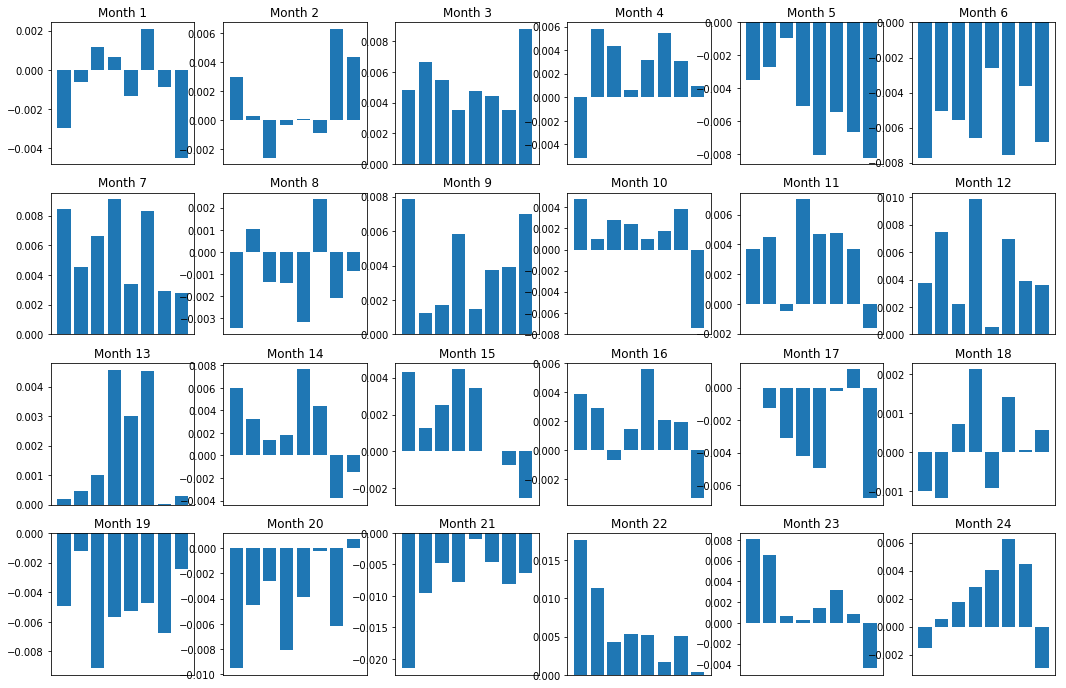
Conséquence des marges (de base)

Bien sûr, ce ne sont que des relations moyennes. Afin de comprendre à quel point la relation est cohérente et si nous sommes prêts à négocier, nous devrions changer notre approche et notre attitude à son égard au fil du temps. Ensuite, nous examinerons leur marge d'intérêt mensuelle (base) pour les deux années précédentes. Nous pouvons voir plus de changements et mener une analyse plus approfondie pour déterminer si ce score de dynamique peut être négocié.

total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
    temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[month]]
    temp_scores = resampled_scores.loc[monthly_index[month-1]:monthly_index[month]]
    for m in temp_returns.index.intersection(temp_scores.index):
        basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
        mean_basket_returns += basket_returns
    
    strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
    
    mean_basket_returns /= temp_returns.index.intersection(temp_scores.index).size
    
    r = int(np.floor((month-1) / 6))
    c = (month-1) % 6
    axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
    axarr[r, c].xaxis.set_visible(False)
    axarr[r, c].set_title('Month ' + str(month))
plt.show()

plt.figure(figsize=(15,7))
plt.plot(strategy_returns)
plt.ylabel('Returns')
plt.xlabel('Month')
plt.plot(strategy_returns.cumsum())
plt.legend(['Monthly Strategy Returns', 'Cumulative Strategy Returns'])
plt.show()

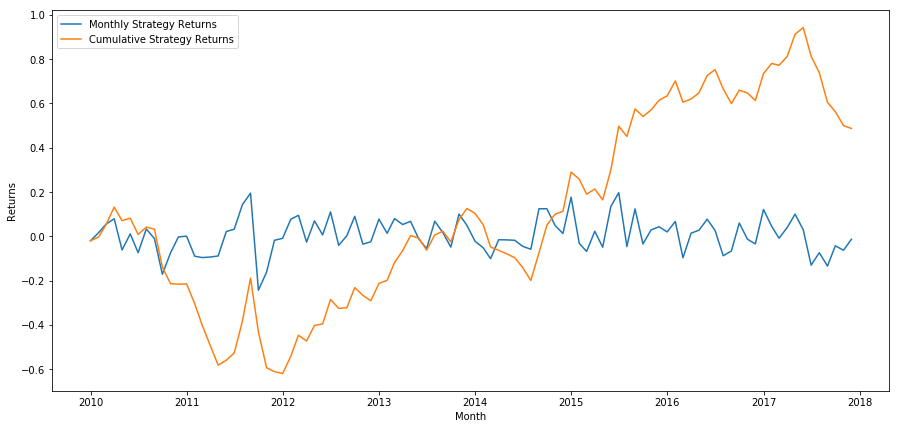
Enfin, si nous allons long le dernier panier et short le premier panier chaque mois, alors regardons les rendements (en supposant une allocation de capital égale par titre).

total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

Taux de rendement annuel: 5,03%

Nous pouvons voir que nous avons un système de classement très faible, qui ne peut distinguer que doucement les stocks à haut rendement des stocks à faible rendement.

Trouver le bon système de classement

Pour réaliser la stratégie d'équité équilibrée à court terme, en fait, vous n'avez qu'à déterminer le schéma de classement. Tout après cela est mécanique. Une fois que vous avez une stratégie d'équité équilibrée à long terme, vous pouvez échanger différents facteurs de classement sans grand changement. C'est un moyen très pratique d'itérer vos idées rapidement sans vous soucier d'ajuster tout le code à chaque fois.

Le schéma de classement peut également provenir de presque n'importe quel modèle. Ce n'est pas nécessairement un modèle facteur basé sur la valeur. Il peut s'agir d'une technologie d'apprentissage automatique qui peut prédire les rendements un mois à l'avance et classer en fonction de ce niveau.

Sélection et évaluation du système de classement

Le système de classement est l'avantage et la partie la plus importante de la stratégie équilibrée d'actions à long terme.

Un bon point de départ est de sélectionner les technologies connues existantes et de voir si vous pouvez les modifier légèrement pour obtenir des rendements plus élevés.

• Clone et ajustement: Choisissez un sujet qui est souvent discuté et voyez si vous pouvez le modifier légèrement pour en tirer des avantages. Généralement, les facteurs disponibles au public n'auront plus de signaux de trading, car ils ont complètement arbitragé hors du marché. Mais parfois, ils vous conduiront dans la bonne direction.

• Modèle de tarification: tout modèle qui prédit les rendements futurs peut être un facteur qui peut potentiellement être utilisé pour classer votre panier d'objets de trading.

• Les facteurs basés sur les prix (indicateurs techniques): les facteurs basés sur les prix, comme discuté aujourd'hui, obtiennent des informations sur le prix historique de chaque action et l'utilisent pour générer des valeurs de facteurs.

• Régression et dynamique: Il convient de noter que certains facteurs pensent qu'une fois que les prix se déplacent dans une direction, ils continueront à le faire, tandis que certains facteurs sont tout le contraire.

• Facteur de base (basé sur la valeur): Il s'agit d'une combinaison de valeurs de base, telles que le PE, les dividendes, etc. La valeur de base contient des informations relatives aux faits réels de l'entreprise, elle peut donc être plus puissante que le prix à bien des égards.

En fin de compte, le prédicteur de développement est une course aux armements, et vous essayez de rester un pas en avant. Les facteurs seront arbitrage du marché et ont une vie utile, donc vous devez constamment travailler pour déterminer combien de récessions vos facteurs ont connu et quels nouveaux facteurs peuvent être utilisés pour les remplacer.

Autres considérations

• Fréquence de rééquilibrage

Chaque système de classement prédit des rendements dans un laps de temps légèrement différent. La régression moyenne basée sur le prix peut être prévisible en quelques jours, tandis que le modèle de facteur basé sur la valeur peut être prédictif en quelques mois. Il est important de déterminer la plage de temps que le modèle devrait prédire et d'effectuer une vérification statistique avant d'exécuter la stratégie. Bien sûr, vous ne voulez pas trop vous adapter en essayant d'optimiser la fréquence de rééquilibrage. Vous trouverez inévitablement une fréquence aléatoire qui est meilleure que les autres fréquences. Une fois que vous avez déterminé la plage de temps de la prédiction du schéma de classement, essayez de rééquilibrer à environ cette fréquence pour tirer pleinement parti de votre modèle.

• Capacité en capital et coûts de transaction

Chaque stratégie a un volume de capital minimum et maximum, et le seuil minimum est généralement déterminé par le coût de la transaction.

Le trading de trop d'actions entraînera des coûts de transaction élevés. Si vous souhaitez acheter 1 000 actions, cela coûtera des milliers de dollars à chaque rééquilibrage. Votre base de capital doit être suffisamment élevée pour que les coûts de transaction puissent représenter une petite partie des rendements générés par votre stratégie. Par exemple, si votre capital est de 100 000 $ et que votre stratégie gagne 1% (1 000 $) par mois, tous ces rendements seront consommés par les coûts de transaction. Vous devez exécuter la stratégie avec des millions de dollars de capital pour gagner plus de 1 000 actions.

Le seuil d'actifs le plus bas dépend principalement du nombre d'actions négociées. Cependant, la capacité maximale est également très élevée. La stratégie d'actions équilibrées long-short peut négocier des centaines de millions de dollars sans perdre l'avantage. C'est un fait, car cette stratégie est relativement rare à rééquilibrer. La valeur en dollars de chaque action sera très faible lorsque les actifs totaux sont divisés par le nombre d'actions négociées. Vous n'avez pas à vous soucier de savoir si votre volume de négociation affectera le marché. Supposons que vous négociez 1 000 actions, c'est-à-dire 100 000 000 de dollars. Si vous rééquilibrez l'ensemble du portefeuille chaque mois, chaque action ne négociera que 100 000 $ par mois, ce qui n'est pas suffisant pour être un marché important pour la plupart des titres.

Relationnée

Plus de