इस लेख में, हम Ornstein-Uhlenbeck प्रक्रिया का अवलोकन करेंगे, इसके गणितीय सूत्रों का वर्णन करेंगे, इसे पायथन के साथ लागू करेंगे और इसका अनुकरण करेंगे, और मात्रात्मक वित्त और सिस्टम ट्रेडिंग में कुछ व्यावहारिक अनुप्रयोगों पर चर्चा करेंगे। हम एक अधिक उन्नत यादृच्छिक प्रक्रिया मॉडल का उपयोग करेंगे, जिसे Ornstein-Uhlenbeck (OU) प्रक्रिया कहा जाता है, जिसका उपयोग सममूल्य वापसी व्यवहार प्रदर्शित करने वाले समय-सीमाओं के मॉडलिंग के लिए किया जा सकता है। यह विशेष रूप से व्युत्पन्न मूल्य निर्धारण में ब्याज दर के मॉडलिंग के लिए उपयोगी है, साथ ही साथ सिस्टम ट्रेडिंग के लिए एल्गोरिथम का संचालन करता है।

Ornstein-Uhlenbeck प्रक्रिया क्या है?

Ornstein-Uhlenbeck प्रक्रिया एक निरंतर समय यादृच्छिक प्रक्रिया है, जिसका उपयोग माध्य मान प्रतिगमन व्यवहार को मॉडलिंग करने के लिए किया जाता है। इसका मतलब यह है कि, मानक यादृच्छिक घूर्णन या ब्राउन आंदोलन के विपरीत, जो अनंत रूप से विचलित हो सकता है, OU प्रक्रिया अक्सर समय के साथ दीर्घकालिक औसत पर लौटती है। गणितीय रूप से, OU प्रक्रिया एक विशिष्ट यादृच्छिक अंतर समीकरण (SDE) की व्याख्या है जो इस समान मान प्रतिगमन व्यवहार को नियंत्रित करती है। OU प्रक्रिया का SDE निम्न सूत्र द्वारा दिया गया हैः

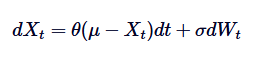
इसमें, Xt समय t में एक यादृच्छिक प्रक्रिया है, μ दीर्घकालिक औसत है, θ औसत वापसी दर है, δ अस्थिरता है, और DWt वाइनेर प्रक्रिया या मानक ब्राउन गति है।

ऐतिहासिक पृष्ठभूमि और अनुप्रयोग

Ornstein-Uhlenbeck प्रक्रिया को मूल रूप से 1930 में Leonard Ornstein और George Eugene Uhlenbeck द्वारा घर्षण की स्थिति में ब्राउन की गति में चलने वाले कणों की गति का अनुकरण करने के लिए प्रस्तावित किया गया था। समय के साथ, इसकी उपयोगिताएं भौतिकी से बहुत आगे बढ़ गई हैं, और इसका उपयोग जीव विज्ञान, रसायन विज्ञान, अर्थशास्त्र और वित्त जैसे विभिन्न क्षेत्रों में किया जाता है।

क्वांटिटेटिव फाइनेंस में, OU प्रक्रिया विशेष रूप से औसत मूल्य वापसी व्यवहार को प्रदर्शित करने वाली घटनाओं को मॉडलिंग करने के लिए उपयोगी है। प्रमुख उदाहरणों में ब्याज दर, विनिमय दर और वित्तीय बाजारों की अस्थिरता शामिल है। उदाहरण के लिए, लोकप्रिय ब्याज दर मॉडल, वासिसेक मॉडल, सीधे OU प्रक्रिया से व्युत्पन्न है।

क्वांटिटेटिव फाइनेंस में महत्व

Ornstein-Uhlenbeck प्रक्रिया मात्रात्मक वित्त में महत्वपूर्ण है, क्योंकि इसकी औसत आवर्ती प्रकृति इसे वित्तीय चर के लिए एक प्राकृतिक विकल्प बनाती है, जो कि यादृच्छिक प्रवासन नहीं करते हैं, लेकिन स्थिरता के आसपास लंबे समय तक औसत मूल्य में उतार-चढ़ाव करते हैं। यह विशेषता ब्याज दर के मॉडलिंग के लिए महत्वपूर्ण है, जिसमें औसत आवर्ती केंद्रीय बैंक के दीर्घकालिक स्थिर ब्याज दर के प्रभाव को दर्शाता है।

इसके अलावा, OU प्रक्रिया का उपयोग परिसंपत्ति मूल्य निर्धारण मॉडल (जिसमें व्युत्पन्न मूल्य निर्धारण शामिल है) और जोखिम प्रबंधन रणनीतियों के लिए किया जाता है। यह अधिक जटिल मॉडल के निर्माण के लिए भी काम कर सकता है, जैसे कि कॉक्स-इंगरसोल-रॉस (CIR) मॉडल, जो OU प्रक्रिया को गैर-नकारात्मक ब्याज दरों के लिए मॉडलिंग करने के लिए विस्तारित करता है।

मुख्य विशेषताएं और अंतर्ज्ञान

Ornstein-Uhlenbeck प्रक्रिया की मुख्य विशेषताओं को इस प्रकार संक्षेप में प्रस्तुत किया जा सकता हैः

• **औसत वापसी:**OU प्रक्रियाओं में दीर्घकालिक औसत पर लौटने की प्रवृत्ति होती है। यह ब्राउन आंदोलन जैसे प्रक्रियाओं के विपरीत है, जो इस प्रवृत्ति को प्रदर्शित नहीं करते हैं।
• **अस्थिरता:**पैरामीटरδ नियंत्रण प्रक्रिया में यादृच्छिकता या अस्थिरता का स्तर. जितनी अधिक अस्थिरता होती है, प्रक्रिया वापसी से पहले औसत से अधिक विचलित होती है।
• वापसी की गतिःपैरामीटरθ प्रक्रिया के वापसी औसत की गति निर्धारित करता है.
• **स्थिरता:**OU प्रक्रिया सुचारू है, जिसका अर्थ है कि इसकी सांख्यिकीय विशेषताएं समय के साथ नहीं बदलती हैं। यह वित्तीय क्षेत्र में स्थिर प्रणालियों के मॉडलिंग के लिए महत्वपूर्ण है।

सहजता से, आप Ornstein-Uhlenbeck प्रक्रिया को एक औसत के आसपास खिंचाव के लिए एक नाड़ी के व्यवहार को मॉडलिंग के रूप में देख सकते हैं। हालांकि यह प्रक्रिया यादृच्छिक उतार-चढ़ाव के कारण औसत से विचलित हो सकती है, नाड़ी के नाड़ी के घर्षण झंझरी (उदाहरण के लिए, औसत पर वापसी) यह सुनिश्चित करता है कि यह अंततः औसत पर वापस आ जाए।

अन्य यादृच्छिक प्रक्रियाओं के साथ तुलना

चूंकि OU प्रक्रिया विभिन्न प्रकार की वित्तीय घटनाओं के मॉडलिंग के साथ निकटता से जुड़ी हुई है, इसलिए इसे अक्सर अन्य यादृच्छिक प्रक्रियाओं (जैसे ब्राउन आंदोलन और ज्यामितीय ब्राउन आंदोलन (GBM)) के साथ तुलना की जाती है। ब्राउन आंदोलन के विपरीत (ब्राउन आंदोलन में कोई वापसी औसत मूल्य की प्रवृत्ति नहीं है), OU प्रक्रिया में स्पष्ट औसत मूल्य वापसी व्यवहार है। यह इसे चर के आसपास स्थिर संतुलन उतार-चढ़ाव के परिदृश्य के लिए मॉडलिंग के लिए अधिक उपयुक्त बनाता है।

GBM की तुलना में, जो आमतौर पर स्टॉक की कीमतों को मॉडलिंग करने के लिए उपयोग किया जाता है और इसमें बहाव और उतार-चढ़ाव वाले तत्व शामिल होते हैं, OU प्रक्रिया सूचकांक वृद्धि नहीं दिखाती है, बल्कि इसके आसपास औसत उतार-चढ़ाव है। GBM समय के साथ बढ़ने वाली संख्याओं को मॉडलिंग करने के लिए अधिक उपयुक्त है, जबकि OU प्रक्रिया उन चरों को मॉडलिंग करने के लिए बहुत उपयुक्त है जो औसत रिटर्न विशेषता दिखाते हैं।

क्वांटम फाइनेंसिंग के उदाहरण

Ornstein-Uhlenbec प्रक्रिया वित्तीय क्षेत्र में व्यापक रूप से लागू होती है, विशेष रूप से मॉडलिंग परिदृश्यों में जहां औसत मूल्य वापसी एक महत्वपूर्ण विशेषता है। नीचे, हम कुछ सबसे आम उपयोग के मामलों पर चर्चा करेंगे।

ब्याज दर मॉडलिंग

OU प्रक्रियाओं के सबसे प्रमुख अनुप्रयोगों में से एक ब्याज दरों का मॉडलिंग है, विशेष रूप से Vasicek मॉडल के ढांचे के भीतर। Vasicek मॉडल मानता है कि ब्याज दर OU प्रक्रियाओं का पालन करती है, यानी ब्याज दरें समय के साथ दीर्घकालिक औसत पर लौटती हैं। यह विशेषता ब्याज दर के व्यवहार को सटीक रूप से अनुकरण करने के लिए महत्वपूर्ण है, क्योंकि ब्याज दरें अनिश्चित काल तक नहीं चलती हैं, बल्कि आर्थिक परिस्थितियों के प्रभाव से औसत स्तर के आसपास उतार-चढ़ाव करती हैं।

संपत्ति मूल्य निर्धारण

परिसंपत्ति मूल्य निर्धारण में, विशेष रूप से निश्चित आय वाली प्रतिभूतियों में, OU प्रक्रिया का उपयोग आमतौर पर बॉन्ड की प्रतिफल दर के विकास का अनुकरण करने के लिए किया जाता है। OU प्रक्रिया की औसत आवर्ती प्रकृति यह सुनिश्चित करती है कि प्रतिफल दर अपने ऐतिहासिक औसत मूल्य से बहुत दूर नहीं जाती है, जो कि देखे गए बाजार व्यवहार के अनुरूप है। यह OU प्रक्रिया को बॉन्ड और अन्य ब्याज दर संवेदनशील उपकरणों के मूल्य निर्धारण के लिए एक मूल्यवान उपकरण बनाता है।

जोड़ी ट्रेडिंग रणनीति

जोड़ी ट्रेडिंग एक बाजार-तटस्थ रणनीति है जिसमें दो संबंधित परिसंपत्तियों में एक ऑफसेट स्थिति स्थापित करना शामिल है। इस मामले में, OU प्रक्रिया विशेष रूप से उपयोगी है क्योंकि यह दो परिसंपत्तियों के बीच के मूल्य अंतर को मॉडलिंग कर सकती है, और मूल्य अंतर आमतौर पर औसत पर वापसी होती है। OU प्रक्रिया का उपयोग करके मूल्य अंतर को मॉडलिंग करके, व्यापारी लाभप्रद प्रवेश और निकास बिंदुओं की पुष्टि कर सकते हैं जब कीमतें अपने औसत से विचलित होती हैं, और औसत पर वापसी की भविष्यवाणी कर सकती हैं, जिससे व्यापार संकेत उत्पन्न होते हैं।

उदाहरण के लिए, यदि दो फ्यूचर्स के बीच का अंतर किसी मूल्यह्रास से अधिक हो जाता है, तो एक व्यापारी उत्कृष्ट प्रदर्शन करने वाले फ्यूचर्स को बंद कर सकता है और खराब प्रदर्शन करने वाले फ्यूचर्स को बंद कर सकता है, उम्मीद है कि अंतर अपने ऐतिहासिक औसत स्तर पर वापस आ जाएगा, जिससे रिवर्स होने पर मुनाफा होगा।

Ornstein-Uhlenbeck SDE का हल

Ornstein-Uhlenbeck प्रक्रिया का विभेदक समीकरण सूत्र इसके समाधान का आधार है. इस SDE को हल करने के लिए, हमने समाकलन कारक विधि का उपयोग किया है. चलो SDE को फिर से लिखेंः

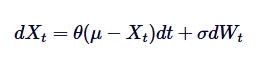
सबसे पहले, हम 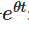के पूर्णांक कारक से दोनों पक्षों को गुणा करते हैंः

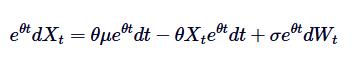
ध्यान दें कि यदि हम दोनों तरफ 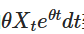जोड़ते हैं, तो बाएं को गुणांक के अंतर के रूप में दर्शाया जा सकता हैः

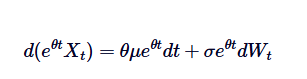
हम 0 से t तक दोनों पक्षों को समाहित करते हैं, और हम प्राप्त करते हैंः

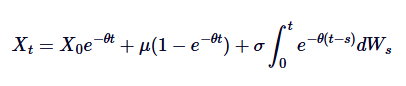
यह Ornstein-Uhlenbeck SDE के लिए सामान्य व्याख्या है।

उपरोक्त निष्कर्ष के स्पष्ट समाधान के कई महत्वपूर्ण अर्थ हैं। पहला 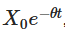है कि प्रारंभिक मूल्य समय के साथ कम हो जाता है, यह दर्शाता है कि प्रक्रिया कैसे धीरे-धीरे भूल जाती है कि यह कहाँ से शुरू हुआ था। दूसरा 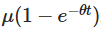है कि प्रक्रिया समय के साथ औसत पर जाती है। तीसरा आइटम यादृच्छिकता का परिचय देता है, जिसमें वाइनेर की प्रक्रिया के पूर्णांक यादृच्छिक उतार-चढ़ाव की व्याख्या करते हैं।

इस समाधान में निश्चितता के औसत मूल्य के प्रतिगमन व्यवहार और ब्राउन आंदोलन द्वारा संचालित यादृच्छिक गुणांक के बीच संतुलन पर जोर दिया गया है। इस समाधान को समझना ओयू प्रक्रियाओं के प्रभावी रूप से अनुकरण करने के लिए महत्वपूर्ण है, जैसा कि नीचे बताया गया है।

अन्य यादृच्छिक प्रक्रियाओं के साथ संबंध

Ornstein-Uhlenbeck प्रक्रिया अन्य प्रसिद्ध यादृच्छिक प्रक्रियाओं के साथ कई महत्वपूर्ण संबंध है, जिसमें ब्राउन आंदोलन और वासिसेक मॉडल शामिल हैं।

ब्राउन आंदोलन के साथ संबंध

ऑर्नस्टीन-उलेनबेक प्रक्रिया को ब्राउन आंदोलन का एक माध्य-वापसी संस्करण माना जा सकता है। ब्राउन आंदोलन एक स्वतंत्र-वृद्धिशील और बिना-वापसी माध्य-वापसी की प्रवृत्ति वाली प्रक्रिया को दर्शाता है, जबकि OU प्रक्रिया ब्राउन आंदोलन को संशोधित करने के लिए बहाव के पदों का उपयोग करके माध्य-वापसी को पेश करती है, जिससे प्रक्रिया को केंद्र-वापसी में वापस खींच लिया जाता है। गणितीय रूप से, यदि हमθ = 0 सेट करते हैं, तो OU प्रक्रिया को मानक ब्राउन आंदोलन के रूप में सरल किया जाता है, जिसमें उतार-चढ़ाव होता हैः

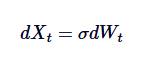
इस प्रकार, ब्राउन आंदोलन OU प्रक्रिया का एक विशेष उदाहरण है, जो माध्य मान रिटर्न की अनुपस्थिति के अनुरूप है।

वासेक मॉडल के साथ संबंध

Vasicek मॉडल को व्यापक रूप से ब्याज दर मॉडलिंग के लिए उपयोग किया जाता है, जो मूल रूप से ब्याज दर के विकास में Ornstein-Uhlenbeck प्रक्रिया का अनुप्रयोग है। Vasicek मॉडल ब्याज दर को OU प्रक्रिया का पालन करने के लिए मानता है, जिसमें SDE को परिभाषित किया गया हैः

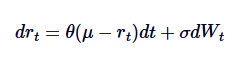
इसमें, rt अल्पकालिक ब्याज दर को दर्शाता है, और पैरामीटर θ, μ और δ की व्याख्या OU प्रक्रिया में व्याख्या के समान है। वासिसेक मॉडल ब्याज दर पथ के लिए औसत मूल्य वापसी का उत्पादन करने में सक्षम है, जो वित्तीय मॉडलिंग में इसके मुख्य लाभों में से एक है।

इन रिश्तों को समझने से यह समझने में मदद मिलती है कि OU प्रक्रिया का उपयोग विभिन्न वातावरणों में कैसे किया जाता है, विशेष रूप से वित्तीय क्षेत्र में। हम नीचे दिए गए उदाहरणों पर चर्चा करते समय इन रिश्तों के व्यावहारिक अर्थों पर चर्चा करेंगे।

Ornstein-Uhlenbeck प्रक्रिया को पायथन के साथ अनुकरण करना

इस अनुभाग में, हम पायथन का उपयोग करने के लिए Ornstein-Uhlenbeck () OU) प्रक्रियाओं का अनुकरण करने के बारे में चर्चा करेंगे। यह OU प्रक्रियाओं को परिभाषित करने के लिए Euler-Maruyama विखंडन का उपयोग करने के लिए एक यादृच्छिक सूक्ष्म विखंडन समीकरण () SDE) शामिल है।

SDE का विखंडन

आइए हम ऊपर दिए गए एसडीई गणितीय सूत्रों की समीक्षा करें और प्रत्येक शब्द का अवलोकन करेंः

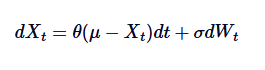
में,

• Xt समय t पर प्रक्रिया का मान है.
• θ औसत वापसी की गति है.
• μ प्रक्रिया का दीर्घकालिक औसत है.
• δ अस्थिरता की दर है.
• dWt वीनर प्रक्रियाओं की वृद्धि को दर्शाता है।

कंप्यूटर पर इस प्रक्रिया का अनुकरण करने के लिए, हमें निरंतर समय SDE का विखंडन करने की आवश्यकता है। एक आम तौर पर इस्तेमाल की जाने वाली विधि Euler-Maruyama विखंडन है, जो छोटे विखंडन समय चरणों 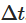को ध्यान में रखते हुए निरंतर प्रक्रिया को करीब से प्रस्तुत करती है। Ornstein-Uhlenbeck प्रक्रिया का विखंडन निम्न फलन द्वारा दिया गया हैः

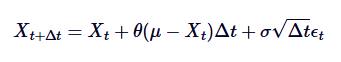
इसमें, 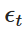मानक सामान्यीकृत वितरण से निकाला गया एक यादृच्छिक चर है (यानी 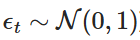) । यह विखंडन हमें समय के साथ Xt के मानों की गणना करने की अनुमति देता है, जिससे OU प्रक्रिया का व्यवहार किया जा सकता है।

पायथन कार्यान्वयन

अब हम पायथन के साथ Ornstein-Uhlenbeck प्रक्रिया को अलग-थलग करने की कोशिश करते हैं। नीचे हम केवल NumPy और Matplotlib पायथन लाइब्रेरी का उपयोग करेंगे।

सबसे पहले, हम NumPy और Matplotlib को मानक तरीके से आयात करते हैं। इसके बाद, हम OU मॉडल के लिए सभी पैरामीटर निर्दिष्ट करते हैं। इसके बाद, हम पहले से ही एक NumPy सरणी की लंबाई N को आवंटित करते हैं, ताकि OU पथ की गणना करने के बाद इसे इसमें जोड़ा जा सके। फिर हम N-1 को पुनरावृत्त करते हैं (चरण 1 निर्दिष्ट प्रारंभिक शर्त X0 है), यादृच्छिक वृद्धि dW का अनुकरण करते हैं, और फिर OU पथ की अगली पुनरावृत्ति की गणना ऊपर दिए गए गणितीय सूत्रों के अनुसार करते हैं। अंत में, Matplotlib का उपयोग करके पथ का इतिहास तैयार करें।

            
            
            
import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 10.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

यह चित्र इस प्रकार है:

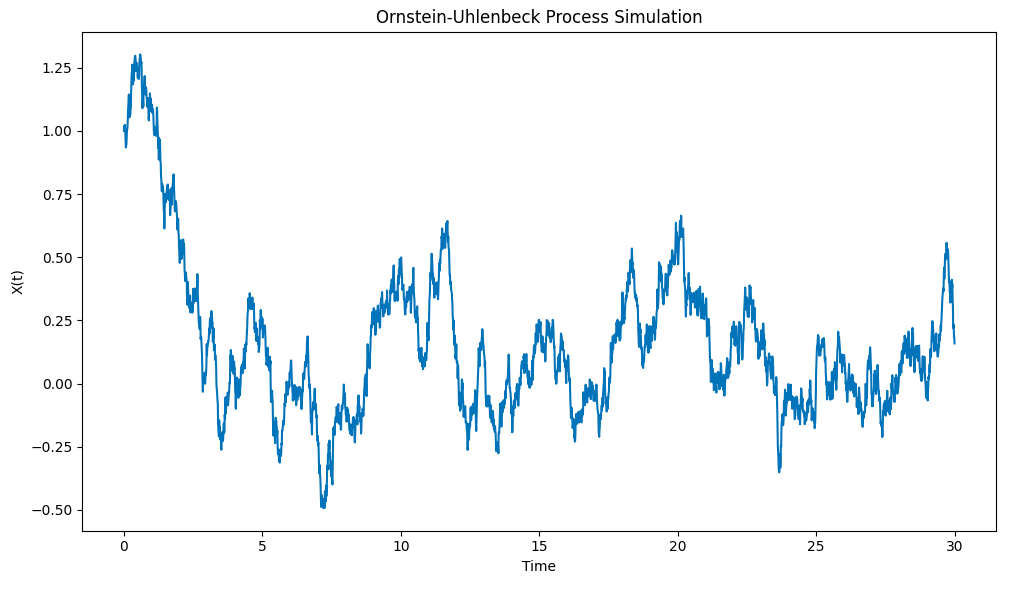
Python के साथ Ornstein-Uhlenbeck प्रक्रिया का अनुकरण

ध्यान दें कि यह प्रक्रिया कैसे प्रारंभिक स्थिति से जल्दी से X0 = 1 को औसत मान μ = 0 तक खींचती है, और फिर जब यह उस औसत मान से विचलित होती है, तो यह उस औसत मान पर लौटने की प्रवृत्ति को प्रदर्शित करती है।

सारांश और आगे के कदम

इस लेख में, हमने Ornstein-Uhlenbeck प्रक्रिया का अवलोकन किया, इसके गणितीय सूत्रों का वर्णन किया, और निरंतर समय SDE के एक अलग संस्करण का अनुकरण करने के लिए पायथन के बुनियादी कार्यान्वयन प्रदान किए। बाद के लेखों में, हम OU प्रक्रियाओं पर आधारित अधिक जटिल SDE का अध्ययन करेंगे, यह जानने के लिए कि वे सिस्टम ट्रेडिंग और व्युत्पन्न मूल्य निर्धारण अनुप्रयोगों के लिए कैसे उपयोग किए जाते हैं।

पूरा कोड

            
            
            
# OU process simulation

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 30.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

मूल लेख का लिंकः https://www.quantstart.com/articles/ornstein-uhlenbeck-simulation-with-python/