कुछ प्रोग्रामेटिक लेनदेन मॉडल के लिए पैरामीटर अनुकूलन के बारे में बात करें

कुछ प्रोग्रामेटिक लेनदेन मॉडल के लिए पैरामीटर अनुकूलन के बारे में बात करें

• पैरामीटर पठार और पैरामीटर द्वीप

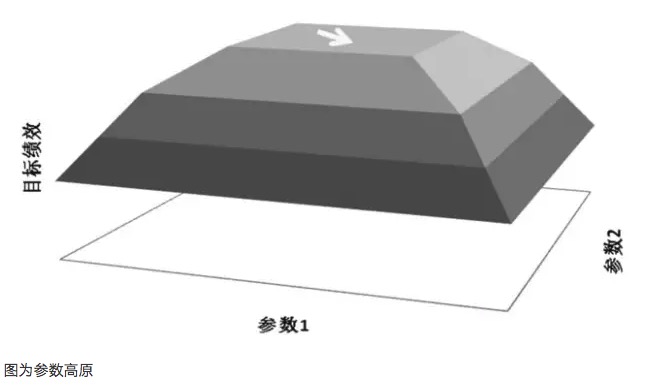
पैरामीटर अनुकूलन में एक महत्वपूर्ण सिद्धांत पैरामीटर प्लेन के बजाय पैरामीटर आइसोलेट की तलाश करना है। पैरामीटर प्लेन कहा जाता है, एक व्यापक पैरामीटर सीमा है, मॉडल इस पैरामीटर सीमा के भीतर बेहतर परिणाम प्राप्त कर सकते हैं, और आम तौर पर एक उच्च मैदान के केंद्र के साथ एक लगभग सामान्य वितरण का गठन करता है। और पैरामीटर आइसोलेट कहा जाता है, मॉडल बेहतर प्रदर्शन करता है जब पैरामीटर मान एक बहुत ही छोटी सीमा में है, और जब पैरामीटर इस मूल्य से विचलित होता है, तो मॉडल की अभिव्यक्ति काफी भिन्न होती है।

• मानचित्र के लिए पैरामीटर पठार

  उदाहरण के लिए, मान लीजिए कि एक ट्रेडिंग मॉडल में दो पैरामीटर हैं, पैरामीटर 1 और पैरामीटर 2, और जब दो पैरामीटरों के लिए क्रॉस-टेस्ट किया जाता है, तो एक तीन आयामी प्रदर्शन चित्र प्राप्त होता है। एक अच्छा पैरामीटर वितरण पैरामीटर प्लैटिनम मानचित्र होना चाहिए, और यहां तक कि जब पैरामीटर सेटिंग्स विचलित होती हैं, तो मॉडल का लाभ प्रदर्शन अभी भी गारंटीकृत होता है। इस तरह के पैरामीटर की स्थिरता के कारण, मॉडल को भविष्य के वास्तविक युद्ध में सभी प्रकार के व्यवहारों का सामना करने के लिए अधिक उत्तरदायी बनाया जा सकता है।

  

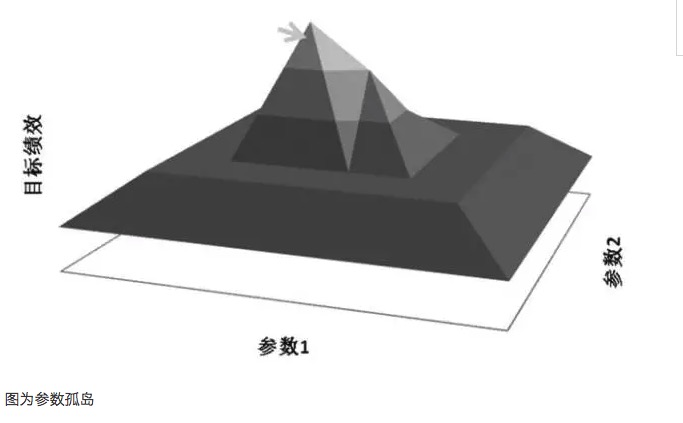
  आम तौर पर, यदि निकटतम पैरामीटर प्रणाली का प्रदर्शन सबसे अच्छा पैरामीटर से बहुत अलग है, तो यह सबसे अच्छा पैरामीटर अत्यधिक समापन का परिणाम हो सकता है, जिसे गणितीय रूप से अजीब समाधान माना जा सकता है, न कि बहुत बड़ा समाधान। गणितीय रूप से, अजीब अस्थिर है, और भविष्य की अनिश्चितता में, एक बार जब बाजार की विशेषताएं बदल जाती हैं, तो सबसे अच्छा पैरामीटर सबसे खराब पैरामीटर बन सकता है।

  अति-अनुकूलन से संबंधित है, यदि चयनित नमूना बाजार की समग्र विशेषताओं का प्रतिनिधित्व नहीं कर सकता है, तो केवल परीक्षण के परिणामों को सकारात्मक अपेक्षित मूल्य तक लाने के लिए पैरामीटर को समायोजित करना, यह निश्चित रूप से एक आत्म-धोखा है, जो पैरामीटर के मूल्य को अति-अनुकूलन के अमान्य पैरामीटर के रूप में प्राप्त करता है। उदाहरण के लिए, पैरामीटर अति-अनुकूलन का विश्लेषण करके, ट्रेडिंग मॉडल में 35 और 63 के मानों पर लाभप्रदता में वृद्धि हुई है। यदि मॉडल में संबंधित संकेतकों को 35 और 63 के रूप में पैरामीटर के रूप में चुना जाता है, तो मॉडल की आय एकदम सही लगती है, लेकिन वास्तव में एक विशिष्ट पैरामीटर द्वीप प्रभाव है।

  अति-अनुकूलन और पैरामीटर अनुकूलन का मुख्य विरोधाभास यह है कि मॉडल पैरामीटर अनुकूलन के लिए प्राप्त सर्वोत्तम पैरामीटर केवल ऐतिहासिक डेटा के नमूने पर आधारित है जो पहले से ही हुआ है, जबकि भविष्य के बाजार गतिशील परिवर्तन हैं, जो ऐतिहासिक बाजारों की तुलना में समानताएं और भिन्नताएं हैं। मॉडल डिजाइनरों को मॉडल के लिए सबसे अच्छा प्रदर्शन करने वाले पैरामीटर मिल सकते हैं, लेकिन यह पैरामीटर भविष्य के मॉडल के वास्तविक अनुप्रयोगों में सबसे अच्छा प्रदर्शन नहीं कर सकता है, और यहां तक कि भविष्य के मॉडल युद्ध में सबसे अच्छा प्रदर्शन करने वाले मॉडल पैरामीटर भी खराब प्रदर्शन कर सकते हैं, या यहां तक कि बड़े पैमाने पर नुकसान भी कर सकते हैं। उदाहरण के लिए, एक पैरामीटर का चयन करना जो इतिहास में एक बड़ी लहर को पकड़ सकता है, लेकिन पैरामीटर के मूल्य को सेट करना इसका मतलब यह नहीं है कि मॉडल भविष्य में इतनी अच्छी तरह से प्रदर्शन कर सकता है।

  इसके अलावा, पैरामीटर प्लेन और पैरामीटर आइसोलेशन अक्सर लेनदेन की संख्या के साथ अधिक संबंध रखते हैं। यदि मॉडल की लेनदेन की संख्या कम है, तो अक्सर एक उपयुक्त पैरामीटर बिंदु पाया जा सकता है, जिससे मॉडल इन सभी लेनदेन में लाभान्वित हो जाता है, जो कि पैरामीटर अनुकूलित मॉडल के लाभ में अधिक आकस्मिकता को दर्शाता है। यदि मॉडल की लेनदेन की संख्या अधिक है, तो मॉडल के लाभ की आकस्मिकता कम हो जाती है, जो कि लाभ की अनिवार्यता और नियमितता को अधिक दर्शाता है, तो एक पैरामीटर प्लेन भी होता है। यह पैरामीटर अनुकूलन मॉडल पैरामीटर अनुकूलन के उद्देश्य के लिए किया जाता है।

• पैरामीटर अनुकूलन के तरीके

  पैरामीटर प्लेन और पैरामीटर आइसोलेशन के बारे में जानने के बाद, पैरामीटर अनुकूलन के तरीके महत्वपूर्ण हैं, विशेष रूप से जब मॉडल में कई पैरामीटर होते हैं (जिन्हें पैरामीटर सेट कहा जाता है), तो अक्सर एक पैरामीटर का मूल्य निर्धारण दूसरे पैरामीटर प्लेन के वितरण को प्रभावित करता है। तो पैरामीटर सेट का अनुकूलन कैसे किया जाता है?

  एक तरीका है क्रमिक अभिसरण विधि; यानी पहले एक पैरामीटर को अलग से अनुकूलित किया जाता है, उसके इष्टतम मान को प्राप्त करने के बाद तय किया जाता है, और फिर दूसरे पैरामीटर को अनुकूलित किया जाता है, उसके इष्टतम मान को प्राप्त करने के बाद तय किया जाता है; इस प्रकार लूप करता है, जब तक कि अनुकूलन परिणाम नहीं बदलता है। उदाहरण के लिए, एक सममित क्रॉस-लेन-देन व्यापार मॉडल, दो स्वतंत्र पैरामीटर हैं, उदाहरण के लिए, औसत लघु चक्र N1 और लंबी चक्र N2। पहले N2 को 1 पर तय किया जाता है, N1 के लिए 1 से 100 के बीच के मानों में परीक्षण फ़िल्टर किया जाता है, सबसे अच्छा पैरामीटर पाया जाता है, सबसे अच्छा पैरामीटर 8 और अंतिम रूप से तय किया जाता है; इसके लिए N2 को 1200 के बीच अनुकूलित किया जाता है, सबसे अच्छा मूल्य 26 और अंतिम रूप से तय किया जाता है; फिर N1 के लिए दूसरे दौर का अनुकूलन किया जाता है, एक नया सबसे अच्छा मूल्य 10 और अंतिम रूप से तय किया जाता है; अंत में N2 के लिए अनुकूलन किया जाता है और अंतिम रूप से अनुकूलित किया जाता है।

  एक अन्य विधि यह है कि एक प्रोग्रामेटिक सॉफ्टवेयर डिजाइन प्लेटफॉर्म का उपयोग करना, जिसमें मजबूत गणना क्षमताएं हैं, सीधे लक्ष्य फ़ंक्शन और पैरामीटर सरणी के बीच वितरण की गणना करें, और फिर बहुआयामी अंतर के वितरण का पता लगाएं, एक अंतर सीमा को परिभाषित करें, जिसमें बहुआयामी वॉल्यूम का सबसे बड़ा, बहुआयामी आंतरिक गोलाकार त्रिज्या का सबसे बड़ा, जो सीमा से कम है, सबसे स्थिर पैरामीटर लेने के लिए चुना जाता है।

  पैरामीटर अनुकूलन के अलावा, डेटा नमूना चयन भी एक महत्वपूर्ण कारक है। ट्रेंड ट्रैक करने वाले मॉडल ट्रेंडिंग बाजारों में बेहतर प्रदर्शन करते हैं, और उच्च-बेचने वाले रणनीतियाँ उतार-चढ़ाव वाले बाजारों में बेहतर प्रदर्शन करती हैं। इसलिए, पैरामीटर अनुकूलन के दौरान, लाभ के लिए अनुकूल ट्रेडिंग विचारों को ठीक से हटाने की आवश्यकता होती है, और नुकसान के लिए अनुचित रणनीति विचारों को जोड़ने की आवश्यकता होती है।

  स्टॉक फ्यूचर्स के उदाहरण के रूप में, 2010 की शुरुआत और 2014 के उत्तरार्ध में जब चरम बैल बाजार दिखाई दिया, स्टॉक फ्यूचर्स एकतरफा थे। इसमें कोई संदेह नहीं है कि सभी प्रवृत्ति मॉडल अच्छे परिणाम प्राप्त करते हैं। हालांकि, यदि हम इस चरम बाजार डेटा को भी नमूने में डालते हैं और पैरामीटर अनुकूलन करते हैं, तो मॉडल पैरामीटर सबसे अच्छे नहीं हो सकते हैं।

  उदाहरण के लिए, मान लीजिए कि एक मॉडल में दो पैरामीटर हैं, पैरामीटर ए का परीक्षण एकतरफा बाजार समय में बहुत अच्छा है और अन्य समय में सामान्य रूप से प्रदर्शन करता है; दूसरे पैरामीटर बी का परीक्षण एकतरफा बाजार समय में पैरामीटर ए से खराब है, अन्य समय में पैरामीटर ए से बेहतर प्रदर्शन करता है, और सभी समय के बीच वितरण समान है। यहां तक कि यदि पैरामीटर ए पूरे नमूना डेटा के परीक्षण के समग्र संकेतकों में जोखिम-लाभ जैसे कि जोखिम-लाभ पैरामीटर बी से अधिक है, तो भी हम पैरामीटर बी का चयन करना पसंद करते हैं, क्योंकि पैरामीटर बी अपेक्षाकृत अधिक स्थिर है और विशिष्ट नमूने पर निर्भर नहीं करता है।

  संक्षेप में, एक तरफ, एक प्रोग्राम ट्रेडिंग मॉडल के निर्माण में, मॉडल को बेहतर ढंग से अनुकूलित करने के लिए पैरामीटर का उपयोग करके मॉडल को अनुकूलित किया जा सकता है, ताकि मॉडल मूल्य में उतार-चढ़ाव के मॉडल को बेहतर ढंग से अनुकूलित कर सके और निवेश की वापसी में सुधार कर सके; दूसरी ओर, पैरामीटर अनुकूलन के लिए अत्यधिक अनुकूलन को रोकने के लिए, जिससे मॉडल बाजार में बदलाव के लिए उपयुक्तता में काफी कमी आती है।

प्रोग्रामेटिक ट्रेडर से अनुप्रेषित