एलएसटीएम फ्रेमवर्क का उपयोग करके बिटकॉइन की कीमतों का वास्तविक समय में पूर्वानुमान

टिपः यह मामला केवल अध्ययन और अनुसंधान के लिए है और निवेश की सिफारिश नहीं करता है।

बिटकॉइन की कीमत का डेटा समय अनुक्रम पर आधारित है, इसलिए बिटकॉइन की कीमत का पूर्वानुमान ज्यादातर LSTM मॉडल का उपयोग करके किया जाता है।

दीर्घकालिक अल्पकालिक स्मृति (LSTM) एक गहराई से सीखने वाला मॉडल है जो विशेष रूप से समय-क्रम डेटा (या समय/स्थानिक/संरचनात्मक क्रम के साथ डेटा, जैसे कि फिल्म, वाक्य आदि) के लिए उपयुक्त है, जो क्रिप्टोकरेंसी की कीमत की दिशा का अनुमान लगाने के लिए एक आदर्श मॉडल है।

इस लेख में मुख्य रूप से एलएसटीएम के माध्यम से डेटा को अनुकूलित करने के लिए लिखा गया है ताकि बिटकॉइन के भविष्य के मूल्य का अनुमान लगाया जा सके।

आयात करने के लिए उपयोग करने के लिए पुस्तकालय

import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

डेटा विश्लेषण

डेटा लोड

बीटीसी के दैनिक लेनदेन के आंकड़े पढ़ें

data = pd.read_csv(filepath_or_buffer="btc_data_day")

डेटा को देखने के लिए, वर्तमान में कुल 1380 डेटा कॉलम हैं, जिनमें Date, Open, High, Low, Close, Volume (BTC), Volume (Currency) और Weighted Price शामिल हैं।

data.info()

शीर्ष 10 पंक्तियों के आंकड़े देखें

data.head(10)

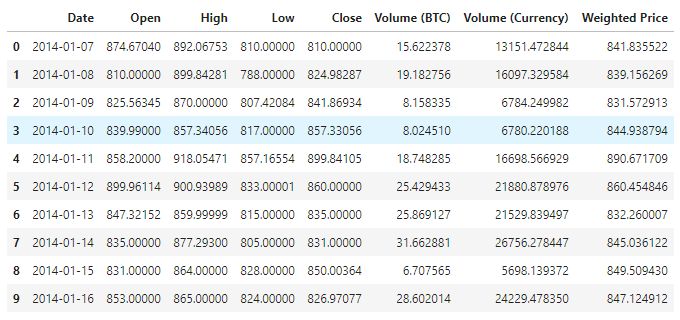
डेटा विज़ुअलाइज़ेशन

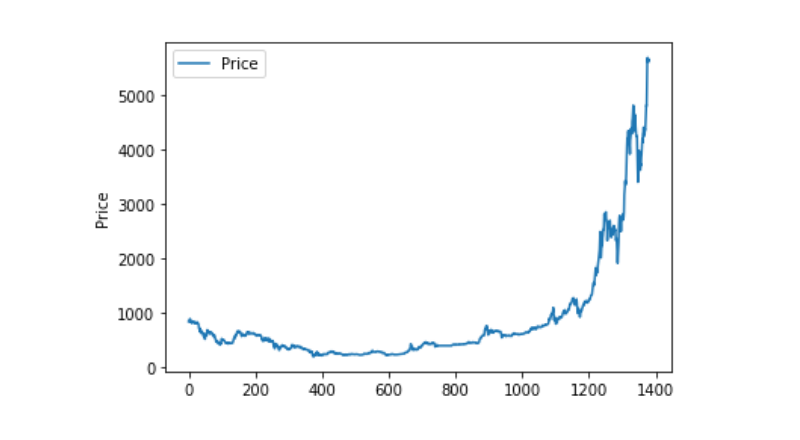
Matplotlib का उपयोग करके Weighted Price को चित्रित किया जाता है, ताकि डेटा का वितरण और रुझान देखा जा सके। चित्र में, हमने एक डेटा 0 का हिस्सा पाया है, और हमें यह पुष्टि करने की आवश्यकता है कि निम्नलिखित डेटा में कोई असामान्यता है या नहीं।

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

असामान्य डेटा प्रसंस्करण

अब हम देखते हैं कि क्या हमारे डेटा में नैनन डेटा है, और हम देख सकते हैं कि हमारे डेटा में नैनन डेटा नहीं है।

data.isnull().sum()

Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

और फिर हम 0 डेटा को देखते हैं, और हम देखते हैं कि हमारे डेटा में 0 है, और हमें 0 के साथ काम करने की आवश्यकता है।

(data == 0).astype(int).any()

Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

(data == 0).astype(int).any()

Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

और फिर आंकड़ों के वितरण और प्रवृत्ति को देखें, और इस समय यह बहुत निरंतर है।

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

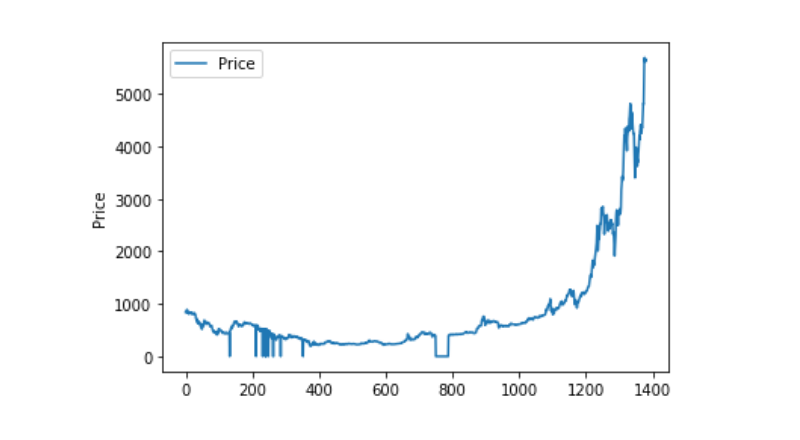
प्रशिक्षण डेटासेट और परीक्षण डेटासेट का विभाजन

डेटा को 0 से 1 में समेकित करें

data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

परीक्षण डेटासेट और प्रशिक्षण डेटासेट को 2:8 से विभाजित करें

ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

हमारे प्रशिक्षण डेटासेट और परीक्षण डेटासेट बनाने के लिए एक दिन के रूप में खिड़की अवधि के लिए प्रशिक्षण डेटासेट और परीक्षण डेटासेट बनाएँ।

def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

मॉडल को परिभाषित करें और प्रशिक्षित करें

इस बार हम एक सरल मॉडल का उपयोग करते हैं, जिसका मॉडल संरचना इस प्रकार है 1. LSTM2. Dense.

इनपुट आकार का आयाम batch_size, time steps, features है। इसमें, time steps का मान डेटा इनपुट के समय का समय खिड़की अंतराल है, यहाँ हम 1 दिन का उपयोग समय खिड़की के रूप में करते हैं, और हमारे डेटा दिन डेटा हैं, इसलिए यहाँ हमारे समय कदम 1 हैं।

लंबी अल्पकालिक स्मृति (एलएसटीएम) एक विशेष प्रकार का आरएनएन है, जो मुख्य रूप से लंबी श्रृंखला प्रशिक्षण के दौरान ग्रिडिएट विलोपन और ग्रिडिएट विस्फोट समस्याओं को हल करने के लिए है।

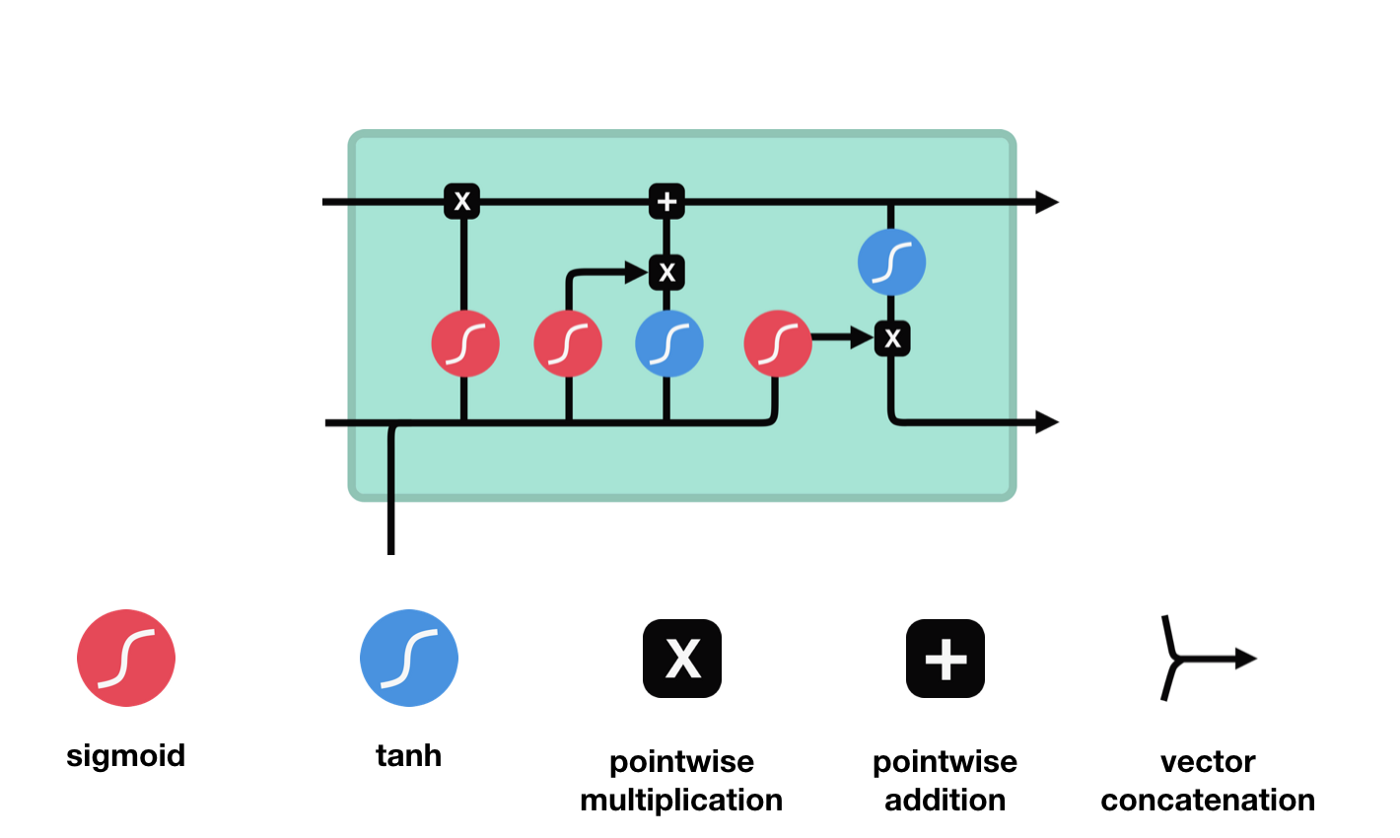
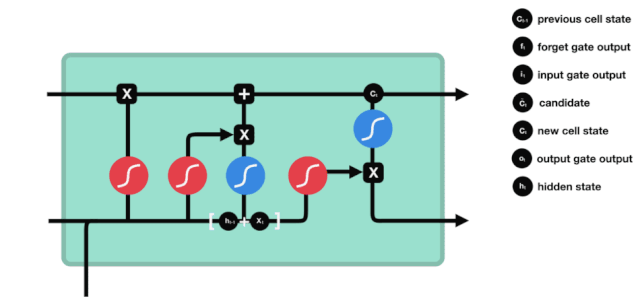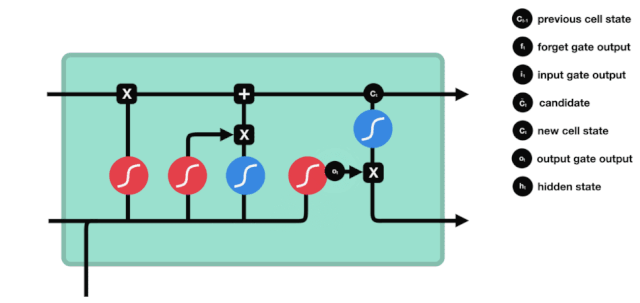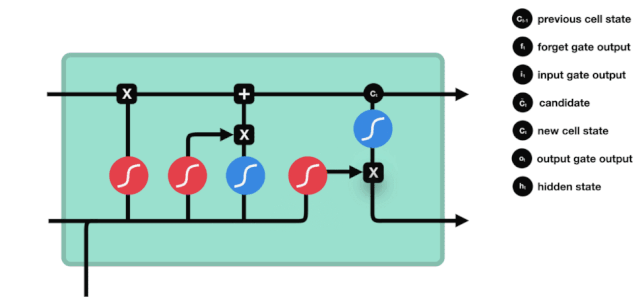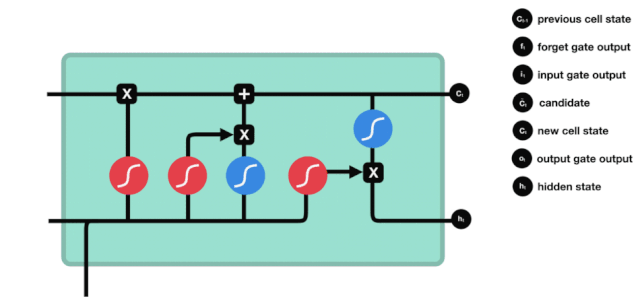
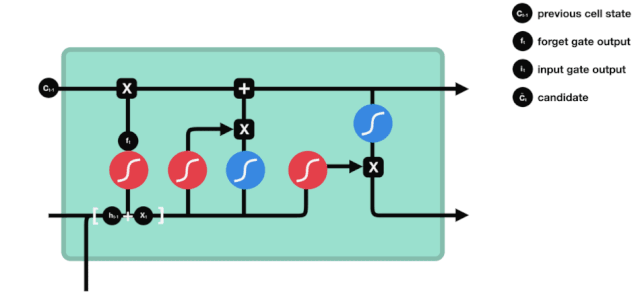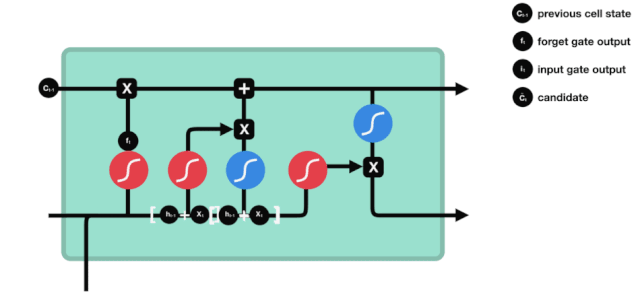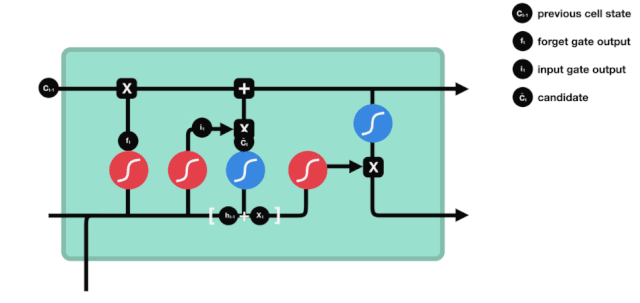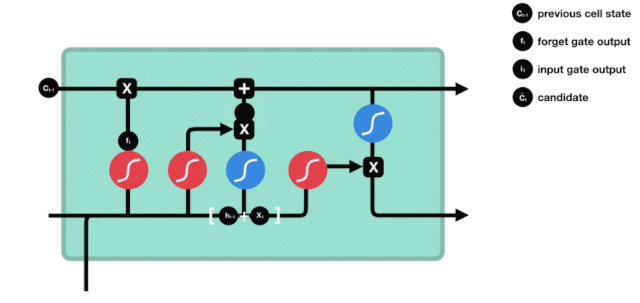
एलएसटीएम के नेटवर्क संरचना चित्र से यह देखा जा सकता है कि एलएसटीएम वास्तव में एक छोटा सा मॉडल है जिसमें 3 सिग्मोइड सक्रियण, 2 टानह सक्रियण, 3 गुणन और 1 जोड़ शामिल हैं।

कोशिकाओं की स्थिति

सेल स्टेटस एलएसटीएम के केंद्र में है, वह ऊपर दी गई रेखा में सबसे ऊपर काली रेखा है, और इस ब्लैक लाइन के नीचे कुछ दरवाजे हैं, जो हम बाद में बताएंगे। सेल स्टेटस प्रत्येक दरवाजे के परिणामों के आधार पर अपडेट किया जाता है। नीचे हम इन दरवाजों का परिचय देते हैं और आप सेल स्टेटस के प्रक्रिया को समझेंगे।

एलएसटीएम नेटवर्क कोशिकाओं की स्थिति के बारे में जानकारी को हटाने या जोड़ने के लिए एक संरचना के माध्यम से कार्य करता है जिसे गेट कहा जाता है। गेट को यह चुनने की क्षमता होती है कि कौन सी जानकारी गुजरती है। गेट की संरचना एक सिग्मोइड परत और एक बिंदु गुणा ऑपरेशन का एक संयोजन है। क्योंकि सिग्मोइड परत का आउटपुट 0 - 1 है, 0 का अर्थ है कि कोई भी नहीं गुजर सकता है, और 1 का अर्थ है कि सभी गुजर सकते हैं। एक एलएसटीएम में तीन द्वार होते हैं जो कोशिकाओं की स्थिति को नियंत्रित करते हैं। हम नीचे एक-एक करके इन द्वारों का परिचय देंगे।

भूल गए द्वार

LSTM का पहला कदम यह तय करना है कि कोशिका की स्थिति को किस सूचना को छोड़ने की आवश्यकता है। यह भाग एक सिग्मोइड इकाई के माध्यम से संसाधित किया जाता है जिसे भूलने का द्वार कहा जाता है।

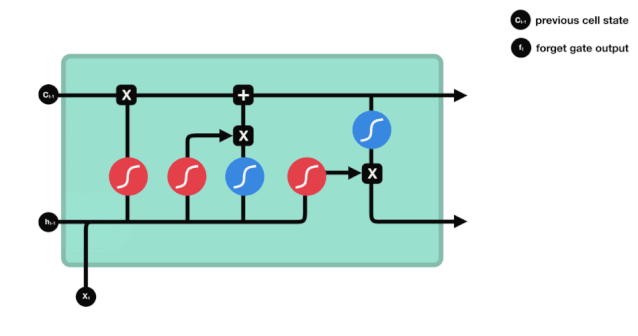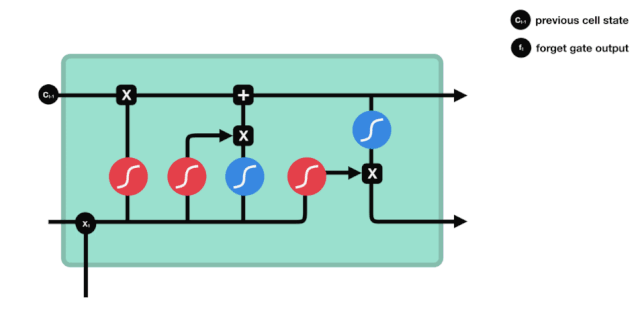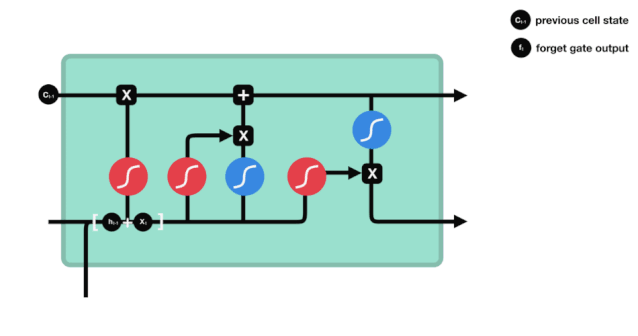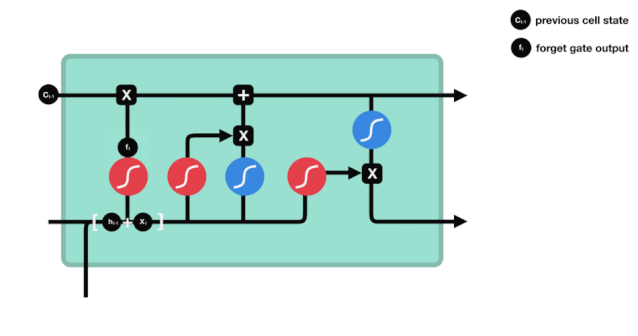
जैसा कि हम देख सकते हैं, भूलने का द्वार $h_{l-1}$ और $x_{t}$ सूचनाओं को देखने से एक 0 से 1 के बीच का एक वेक्टर निकालता है, जिसमें 0 से 1 का मान बताता है कि सेल की स्थिति $C_{t-1}$ में कौन सी सूचनाएं कितनी हैं।

गणितीय अभिव्यक्तिः $f_{t}=\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right) $

प्रवेश द्वार

अगला कदम यह तय करना है कि सेल की स्थिति में कौन सी नई जानकारी जोड़ी जानी चाहिए, यह कदम इनपुट के माध्यम से किया जाता है।

हम देखते हैं कि $h_{l-1}$ और $x_{t}$ की जानकारी को फिर से एक विस्मरण द्वार (sigmoid) और इनपुट द्वार (tanh) में डाला जाता है. क्योंकि विस्मरण द्वार का आउटपुट 0 का मूल्य है, इसलिए यदि विस्मरण द्वार का आउटपुट 0 है, तो इनपुट के बाद का परिणाम $C_{i}$ वर्तमान सेल स्थिति में नहीं जोड़ा जाएगा, यदि यह 1 है, तो यह सब सेल स्थिति में जोड़ा जाएगा, इसलिए यहां विस्मरण द्वार का काम इनपुट द्वार के परिणाम को सेल स्थिति में चयनित रूप से जोड़ना है।

गणितीय सूत्र हैः $C_{t}=f_{t} * C_{t-1} + i_{t} * \tilde{C}_{t} $

बाहर निकलना

सेल की स्थिति को अपडेट करने के बाद, $h_{l-1}$ और $x_{t}$ इनपुट के आधार पर आउटपुट सेल की कौन सी स्थिति विशेषताओं का निर्धारण करने की आवश्यकता होती है, जिसमें इनपुट को सिग्मोइड परत के माध्यम से जाना जाता है जिसे आउटपुट गेट कहा जाता है, और फिर सेल की स्थिति को tanh परत के माध्यम से एक वेक्टर प्राप्त किया जाता है जिसका मान -1 से 1 के बीच होता है, जो वेक्टर आउटपुट गेट द्वारा प्राप्त निर्णय की स्थिति से गुणा करके अंतिम आरएनएन इकाई के आउटपुट को प्राप्त करता है।

def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

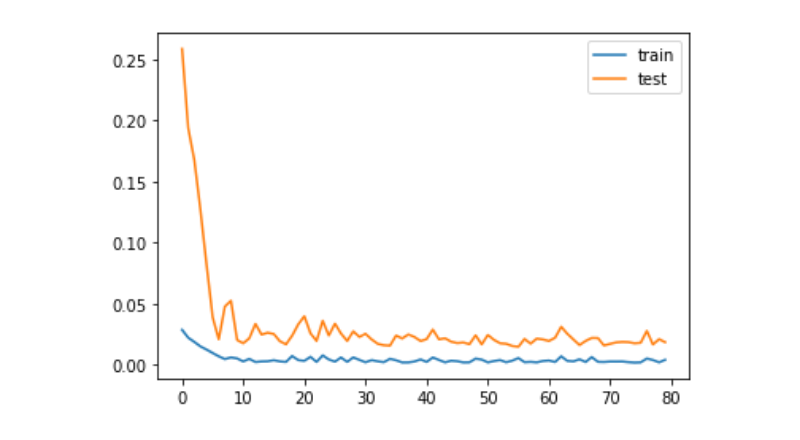
history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

पूर्वानुमान

predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

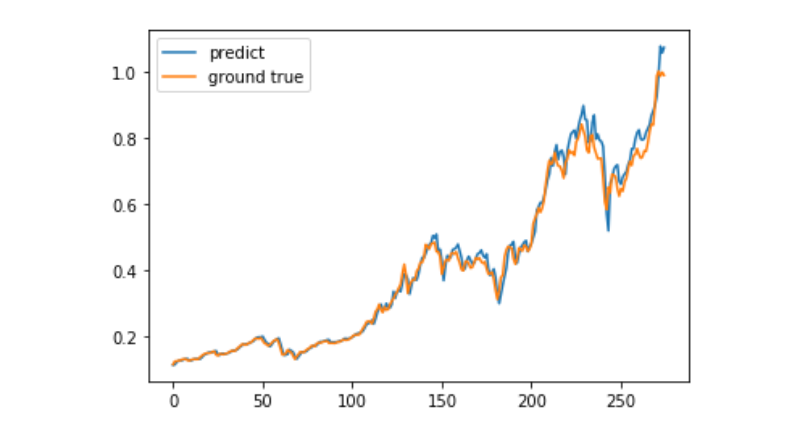
वर्तमान में, मशीन सीखने का उपयोग करके बिटकॉइन की लंबी अवधि की कीमत की भविष्यवाणी करना बहुत मुश्किल है, और यह केवल एक सीखने के मामले के रूप में उपयोग किया जा सकता है। यह मामला बाद में मिक्टर पूल क्लाउड के डेमो के साथ ऑनलाइन होगा, जिसे इच्छुक उपयोगकर्ता सीधे अनुभव कर सकते हैं।