समय का चयन करने की रणनीति का चयन ((1) क्लासिक तकनीकी संकेतक का चयन करते समय Z रूपांतरण के दृष्टिकोण के नीचे कम देरी की प्रवृत्ति रेखा का निर्माण

कुछ समय पहले, किसी ने कहा था कि मैं हर दिन कुत्तों की रणनीति विकसित करता हूं, और हां, कुत्तों की रणनीति समाप्त हो गई है। आज मैं आपको एक कुत्तों की रणनीति साझा करने जा रहा हूं जो हाल ही में इस्तेमाल किया गया है।१. पूर्वाधार ● चलो गंभीरता से बात करते हैं, क्लासिक समय निर्धारण रणनीतियों को वास्तव में कई श्रेणियों में विभाजित किया गया हैः अल्पकालिक घटना संचालित (मॉनेटिक सर्कल में प्रमुख एक्सचेंजों की घोषणाओं और ट्वीट्स की निगरानी के रूप में प्रदर्शित होता है, जो पाठ विश्लेषण से संबंधित है), सांख्यिकीय अर्थों में रिटर्न और पूर्वानुमान (सांख्यिकीय लाभ, संरेखित लेनदेन, विभिन्न प्रकार के एमएल और डीएल मॉडल, स्तरित छिपे हुए मार्कोव आदि), जीएसआईएसआई प्रकार के निवेशकों की भावनाओं का चयन करते समय, और पारंपरिक क्लासिक तकनीकी संकेतकों का चयन करते समय। तकनीकी संकेतकों का उपयोग अधिकांश निवेशकों द्वारा किया जाता है, जो जटिल मॉडल की तुलना में बहुत कम जोखिम के साथ अत्यधिक अनुकूलित होते हैं, लेकिन दोष भी स्पष्ट हैं।

N日移动平均线=N日收盘价之和/N

● आम तौर पर आम निवेशकों द्वारा इसे एक समतल रेखा (MA) के रूप में जाना जाता है, एक समतल रेखा, जो खरीदारी को तोड़ती है, गिरती है, बेचती है, और अनगिनत लोग एक्सचेंजों के लिए अपनी प्रक्रिया शुल्क में योगदान देते हैं। ● समतुल्य रेखाएं कीमतों के आंदोलन को अच्छी तरह से चित्रित कर सकती हैं और इस प्रवृत्ति को बारीकी से ट्रैक कर सकती हैं और आसानी से नहीं बदल सकती हैं। हालांकि, समतुल्य रेखाएं वायदा सीटीए के विकास में एक बहुत ही महत्वपूर्ण संदर्भ सूचक हैं। हालांकि, सामान्य निवेशकों के लिए समतुल्य रेखाओं के उपयोग के साथ कुछ समस्याएं हैंः पहला, समतुल्य रेखाएं गंभीर रूप से विलंबित हैं, अक्सर संकेतों के दौरान प्रवृत्ति का आधा हिस्सा समाप्त हो जाता है और वापस आ जाता है; दूसरा, सिक्का चक्र के सामान्य निवेशक अक्सर अंश-स्तर के संकेतों पर संचालन करते हैं, 15 मिनट, 5 मिनट और यहां तक कि 1 मिनट, इस तरह के छोटे चक्र में, सिक्का चक्र में 80% से अधिक विशेषता वाले उतार-चढ़ाव (मार्टिन की पसंद का प्रकार), बहुत कम घटनाएं होती हैं, और निवेशक बहुत सारे प्रक्रिया शुल्क और स्लाइड पॉइंट खो देते हैं। ● इस लेख का उद्देश्य सभी के लिए संदर्भ और उपयोग के लिए एक एल्गोरिथ्म का निर्माण करना है जो समवर्ती वर्ग के संकेतकों को फ़िल्टर करने और उनके विलंबता को कम करने के लिए है।

2. Z रूपांतरण, संचरण कार्य ● इस लेख से पहले, मैंने विभिन्न प्रमुख वेबसाइटों पर कुछ सूचक फ़िल्टर एल्गोरिदम के बारे में सीखा है, जैसे कि सबसे आम ट्यूरियस फ़िल्टर (जो स्काइडोर ब्रॉडकास्ट के कुछ सीटीए में दिखाई देता है), और जोइनक्वांट पर लेखक द्वारा अध्ययन किए गए कार्लमैन फ़िल्टर विधि ने 2015 के शेयर आपदा से सफलतापूर्वक बचाव किया। टीबी पर ईआर फ़िल्टर मॉड्यूल का उपयोग करना बेहद सुविधाजनक है। हालांकि, जब मैंने पाया कि जोइनक्वांट पर उपलब्ध कार्लमैन फ़िल्टर मॉड्यूल सर्वर में नहीं डाला जा सकता है, और इसका ओपन सोर्स कोड कुछ हजार लाइनों का है, तो उसने इसे सिक्के के घेरे में ले जाने का प्रयास छोड़ दिया। ● Z रूपांतरण लैप्रस से आता है, जो अक्सर गणितीय संकेत प्रसंस्करण के क्षेत्र में उपयोग किया जाता है। एक असतत समय अनुक्रम f ((k) के लिए और बहु-आयामी क्षेत्र में परिभाषित z के लिए, इसका सूत्र इस प्रकार परिभाषित हैः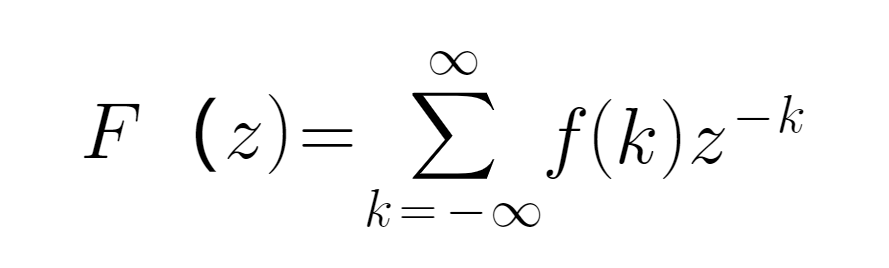

● ईएमए की समोच्च रेखा में एमए की तुलना में कम विलंबता होती है ((मूल रूप से ईडब्ल्यूएमए एल्गोरिथ्म का उपयोग करके एमए अनुक्रमों को संसाधित करने के बाद प्राप्त परिणाम है), इसलिए हम यहां ईएमए अनुक्रमों का उपयोग करते हैं, न कि एमए, ताकि फ़िल्टर का प्रभाव बढ़ सके। हम इनपुट को मुद्राओं के लिए मूल्य के रूप में परिभाषित करते हैं ((बंद कीमत), p के रूप में लिखा जाता है ((z), और आउटपुट को ईएमए सूचकांक के रूप में लिखा जाता है, जिसे ईएमए के रूप में लिखा जाता है ((z)) इसलिए, इस मामले में संचरण फ़ंक्शन, ईएमए और इसके संबंधित संचरण मूल्य के लिए तीव्रता अनुपात है, यह एक प्रतिक्रियाशील प्रणाली है, संचरण फ़ंक्शन एचजेड के रूप में लिखा जाता हैः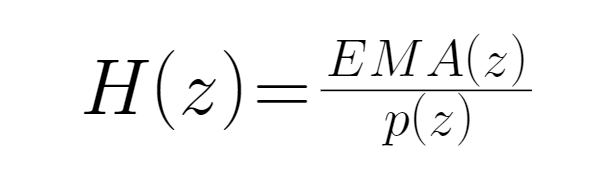

● इस सूत्र को EWMA के एल्गोरिथ्म में डालने से EMA का प्रारंभिक पास फ़ंक्शन प्राप्त होता हैः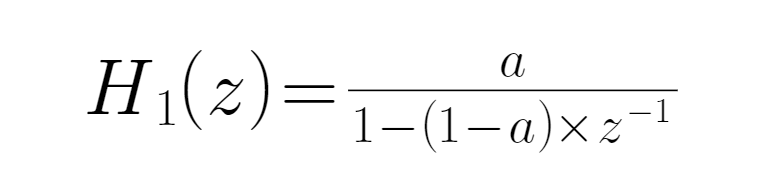

● जिसमें a एक चर है, जो कि एक समान है.

3. संचरण फलन का विश्लेषण ● संचरण फ़ंक्शन में, इनपुट सिग्नल फ़ंक्शन मान से असंबद्ध है. इस फ़ंक्शन के विश्लेषण से यह ज्ञात है कि जब z**-1=-1, H(z) का अधिकतम मान लिया जाता है, जो कि उच्चतम आवृत्ति तक पहुंचता है, संचरण फ़ंक्शन H(z) = a/(2-a है, हाल के उच्च आवृत्ति डेटा का शोर अधिकतम कम हो जाता है; जब z**-1=1 और H(z) एक स्थिर है, तो सिस्टम आवृत्ति 0 है, और इनपुट और आउटपुट परिणाम बिल्कुल समान हैं, यदि इस समय अनुक्रम एक निरंतर अनुक्रम है, तो ईएमए होगा। ● जब H (z) एक निम्न-प्रवाह फ़िल्टर है और H (z) = 1, तो आउटपुट सिग्नल में इनपुट सिग्नल के सभी अंश होते हैं, यानी सभी आउटपुट सिग्नल में से, यदि सभी निम्न-आवृत्ति संकेतों को घटाया जाए, तो 1 - H (z) को एक नए फ़िल्टर के रूप में बनाया जा सकता है, जिसे H (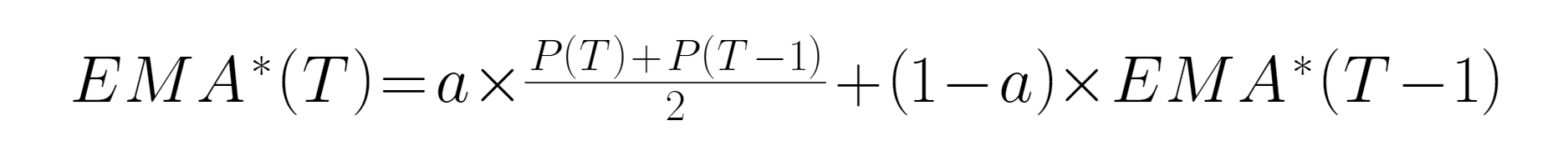) लिखा जाता है, जो H (z) के विपरीत है, जो एक उच्च-प्रवाह फ़िल्टर है। ● P ((T) को रूट k के रूप में लें, हम उस दिन की कीमत और उससे पहले के दिन की कीमत लेते हैं, ताकि इस फंक्शन को सुचारू किया जा सके, जिससे आउटपुट ईएमए में और सुधार हो सके। (यह इसलिए है क्योंकि मूल प्रसारण फ़ंक्शन H ((z) = a/(2-a) के दौरान, उच्च आवृत्ति संकेत को प्रभावी ढंग से फ़िल्टर नहीं किया गया था, इसलिए एक मूल्य पहले लिया गया था ताकि इसे सुचारू किया जा सके, यदि प्रभाव अभी भी बुरा है, तो कई अतिरिक्त भार लिया जा सकता है) इसलिए उस दिन इनपुट किए गए ईएमए संशोधन अभिव्यक्ति हैंः● निम्न-प्रवाह फिल्टर के लिए, उच्च-प्रवाह फिल्टर के लिए अभिव्यक्ति को केवल 1 से कम करने की आवश्यकता हैः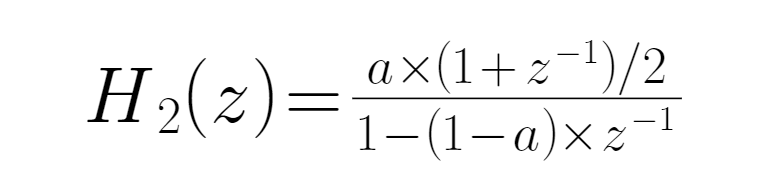● अब फिल्टर के लिए अभिव्यक्ति का निर्माण पूरा हो गया है! Z रूपांतरण के साथ, हम एक कम देरी वाली प्रवृत्ति रेखा का निर्माण कर सकते हैं, और यह केवल एक पैरामीटर a है, a जितना बड़ा होगा, उतना ही कम देरी, बेहतर चिकनाई होगी। विभिन्न किस्मों के लिए अलग-अलग अनुकूलन पैरामीटर हैं।

4. सारांश और ध्यान देने योग्य बातें ● उपर्युक्त चरणों में निर्मित फ़िल्टर केवल एक चरण का होता है, और संक्रमण का समय बहुत लंबा होने के कारण इसका फ़िल्टर प्रभाव बहुत आदर्श नहीं होता है, और चरणों में वृद्धि के बाद, H ((z) फ़ंक्शन अभिव्यक्ति की जटिलता में सूचकांक स्तर की वृद्धि होती है, और अत्यधिक उच्च चरणों में फ़िल्टर एकसमानता की स्थिति में असंगत कूद की संभावना होती है। पिछले अनुभव से, चरण 2 या 3 चरणों के लिए अधिक उपयुक्त हैं, पाठक कई समान या अलग-अलग चरणों के फ़िल्टरों को अपने आप में एक रैखिक संयोजन का उपयोग करके श्रृंखलाबद्ध कर सकते हैं और इसका प्रभाव देख सकते हैं, क्योंकि लेखक सार्वजनिक मामलों में व्यस्त है, इसलिए एक-एक करके परीक्षण करना असंभव है। ● इस Z-परिवर्तन आधारित फ़िल्टरिंग एल्गोरिथ्म का उपयोग न केवल सरलीकृत प्रकार के संकेतकों के लिए किया जाता है, बल्कि सभी संकेतकों के लिए जो झूठे संकेत हैं, जैसे कि बोल और एटीआर, फ़िल्टरिंग एल्गोरिथ्म के माध्यम से एक निश्चित फ़िल्टरिंग प्रभाव प्राप्त कर सकते हैं, जो शुरुआती ट्रेडों को तोड़ने के लिए सीमा का आकार निर्धारित करते हैं, जिससे मूल संकेतकों की देरी के गंभीर बाद के दुष्प्रभावों को कम किया जा सकता है। ● इस लेख का अंत इस तरह है कि यह संबंधित एल्गोरिदम कोड प्रदान करने के लिए समय नहीं लेता है, लेकिन केवल एक विचार देता है, जो रुचि रखने वाले पाठकों को अपने लिए परीक्षण करने के लिए अनुमति देता है।

●प्रोमिस क्वांट मिनो, जो कि मार्टिन के आधार पर विभिन्न प्रकार के शानदार कुत्तों की रणनीतियों के विकास पर केंद्रित है, जैसे कि यदि आपको किराये की आवश्यकता है या बड़ी धनराशि रखने की आवश्यकता है, तो vx:15001733415 पर संपर्क करें