लीक और बोली-मांग प्रसार: EKOP मॉडल पर एक प्रारंभिक अध्ययन

• 1 प्रस्तावना

  हाल ही में असाधारण रूप से व्यस्त, पिछले लेख के बाद से कई महीने बीत चुके हैं। इन महीनों में बहुत सी चीजें हुईं, जिनमें से कुछ मेरी अपनी जिंदगी के लिए एक काला झंडा थे। लेकिन इन अनुभवों ने मुझे सिखाया कि जीवन, व्यापार की तरह, उतार-चढ़ाव और अज्ञात से भरा है। हम हमेशा कुछ सीखने की उम्मीद करते हैं जो पहले से ही हो चुका है और धीरे-धीरे उस सच्चाई के करीब पहुंचते हैं जो शायद मौजूद नहीं है।

  हम सभी जानते हैं कि एक सक्रिय स्टॉक में आमतौर पर एक छोटे से खरीद और बिक्री का अंतर होता है, जबकि एक निष्क्रिय स्टॉक में इसके विपरीत होता है। ऐसा क्यों होता है? क्या एक सरल और सुंदर गणितीय मॉडल के साथ कीमत अंतर की व्याख्या की जा सकती है? आज हम बात करेंगे EKOP मॉडल[1] यह प्रस्ताव शुरू में विभिन्न जानकारी वाले व्यापारियों के व्यवहार के बारे में अध्ययन करने के लिए था कि क्या यह दो प्रकार के शेयरों की कीमतों में अंतर का कारण है। इस स्तंभ लेख में, मैं इस मॉडल की नींव के बारे में बात करूंगा। मॉडल के अनुप्रयोगों का आगे विश्लेषण किया जाएगा (यदि मेरे पास समय है) बाद के लेखों में।

• 2 लेनदेन प्रक्रिया परिकल्पना

  जब हम एक वित्तीय मॉडल के बारे में बात करते हैं, तो सबसे महत्वपूर्ण बात यह है कि इस मॉडल की धारणाओं पर ध्यान दें। एक अच्छा वित्तीय मॉडल अपनी तरह की धारणाएं रखता हैः यह इतना मजबूत नहीं है कि यह सार्वभौमिक नहीं हो सकता है; यह इतना कमजोर नहीं है कि यह सुंदर और संक्षिप्त परिणामों का अनुमान नहीं लगा सकता है। EKOP मॉडल की मूलभूत धारणाएं इस प्रकार हैंः

  परिकल्पना 1: हम शेयरों के कारोबार के बारे में बात कर रहे हैं, व्यापारिक गतिविधि दिन के बीच अलग-अलग है, दिन के भीतर लगातार परिकल्पना। यानी, व्यापारियों की व्यापारिक गतिविधि 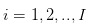इन अलग-अलग व्यापारिक दिनों में से एक पर हुई है। और व्यापारिक दिनों के भीतर, व्यापार 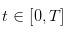इस तरह के निरंतर समय पर हुआ है। आदेश शेयरों के एक समूह के लिए, हर दिन के अंत में शेयरों के मूल्य में परिवर्तन के साथ, हर दिन तीन संभावनाएं हैं

  • बुरी खबर यह है कि हम शेयरों को 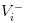के रूप में मूल्यवान करते हैं।
  • अच्छी खबर यह है कि हम शेयरों को /upload/asset/9efe14739d7dad9c5e883e2a0d6b38241a892641 के रूप में लिखते हैं।
  • कोई खबर नहीं है, हम शेयरों के मूल्य को

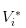
  यह स्पष्ट है कि हमारे पास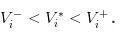

  परिकल्पना 2: किसी दिन,

  की संभावना एक घटना है जो शेयर की कीमत को प्रभावित करती है, तो एक 1-α की संभावना एक घटना है जो शेयर की कीमत को प्रभावित नहीं करती है। उन दिनों में जब एक घटना होती है, तो एकδ की संभावना एक बुरी घटना होती है जो शेयर की कीमत को कम कर देती है, और एक 1-δ की संभावना एक अच्छी चीज होती है जो शेयर की कीमत को बढ़ा देती है।

  परिकल्पना 3: शेयरों के व्यापार में प्रतिभागी बाजार निर्माता, सूचित व्यापारी और अज्ञान व्यापारी होते हैं। वे क्रमशः इस तरह के व्यापार व्यवहार का पालन करते हैंः

  एमएम हमेशा एक इकाई की खरीद या बिक्री के लिए तैयार रहता है, एक बाज़ारिया के रूप में अपनी जिम्मेदारी निभाते हुए। एमएम जोखिम-तटस्थ है, इसलिए वह जिस कीमत पर सूची बनाता है वह वह है जो वह खुद को उचित मानता है।

  आईटी केवल समाचार के दिनों में व्यापार करता है, उनका व्यापार एक आरामदायक प्रक्रिया है। एक दिन, अगर कोई बुरी खबर आती है, तो वह एक विक्रय पत्र को μ की आगमन दर पर लगाता है; और अच्छे समाचार के दिनों में, वह एक खरीद को μ की आगमन दर पर लगाता है।

  यूटी, यानी हमारे गरीब चना, बिना किसी सूचना के लाभ के कारण, उनके लेनदेन की प्रक्रिया भी एक आरामदायक प्रक्रिया है, हर दिन, ईटी के आधार पर, खरीद और बिक्री के लिए भुगतान करते हैं।
  ध्यान दें कि यहाँ पर सभी पोसन प्रक्रियाएं एक-दूसरे से स्वतंत्र हैं। हम परिकल्पना 3 को एक आरेख के साथ प्रदर्शित कर सकते हैं, जैसे किः

  

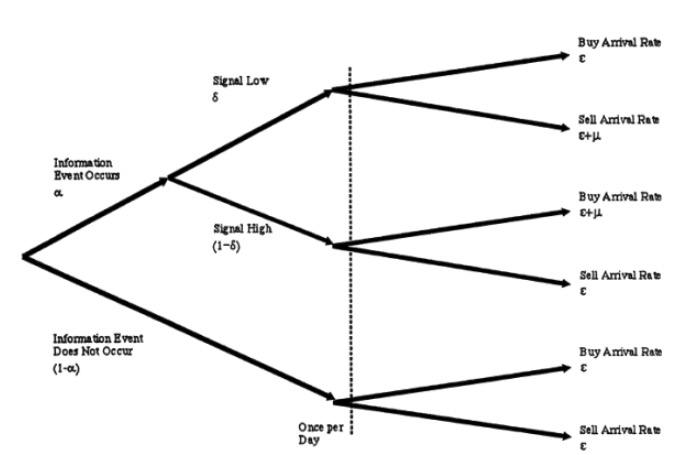
• 3 सौदे और कीमतों का अद्यतन

  हम जानते हैं कि बाजार व्यापारी आमतौर पर बड़ी कंपनियों के लिए काम करते हैं। वे बहुत स्मार्ट हैं, और आईटी और यूटी के साथ लंबे समय तक संघर्ष करते हुए, उन्होंने ऐतिहासिक डेटा के एक बड़े विश्लेषण के माध्यम से ऊपर दिए गए ट्रीग्राफ में सभी मॉडल मापदंडों को संक्षेप में प्रस्तुत किया है। लेकिन, सौभाग्य से, वे एक सूचित व्यापारी के रूप में महान नहीं हैं, और जब एक व्यापारिक दिन शुरू होने वाला है, तो वे व्यापारियों की तरह नहीं जानते हैं कि क्या आज कुछ महत्वपूर्ण हुआ है। वे क्या कर सकते हैं, इस व्यापारिक दिन के व्यापार के दौरान, लगातार अन्य व्यापारियों के बयानों के माध्यम से, अपने आप को अपडेट करें कि क्या आज कुछ अच्छा या बुरा हुआ है (दोस्तों की चेतावनीः उपरोक्त सभी परिकल्पना है) । यह समझना आसान है। विशेष रूप से एक बाजार व्यापारी के रूप में, अगर मुझे लगता है कि आज का दिन विशेष है, तो मैं स्वाभाविक रूप से अनुमान लगाऊंगा कि आज कुछ अच्छा नहीं हुआ है, और इसके विपरीत, मैं अपने आप को इस घटना की संभावना को बढ़ाता हूं; यदि मैं अपने अनुमान को बढ़ाता हूं, तो यह स्वाभाविक रूप से बढ़ जाएगा।

  अब, चलो एक MM के रूप में अनुभव करते हैं, आईटी और यूटी के साथ संघर्ष करते हैं। एक समय t पर, हम अपने आप को कुछ भी नहीं, कुछ अच्छा, और कुछ बुरा होने की संभावना के बारे में अनुमान के लिए एक वेक्टर के रूप में याद करते हैं।

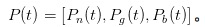  。 यह स्पष्ट है कि दिन की शुरुआत में, जब 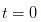था, मैंने एक भी नोट नहीं देखा था, इसलिए मैं यह मान सकता हूं कि कुछ भी नहीं होने की संभावना α है, अच्छी घटनाओं की संभावना 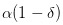है, और बुरी घटनाओं की संभावना है।

  अब हम इस संभावना को कैसे अद्यतन कर सकते हैं? ठीक है, हम जो बाजार के चयनकर्ता हैं, हम सभी बेयज़ के सूत्र को जानते हैं। जब हम देखते हैं कि एक बिका हुआ है, तो हम बेयज़ के नियम का उपयोग करते हैं और अपने स्वयं के संभावना अनुमान को अद्यतन करते हैं। हम सबसे पहले आज की खबर के लिए संभावना अनुमान को अद्यतन करते हैं, जो इस प्रकार है

  

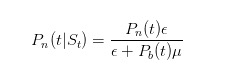
  इस सूत्र का तात्पर्य यह है कि जब कोई खबर नहीं होती है, तो केवल अनजान व्यापारी ही ई के तहत एक बोली बेचते हैं; और विभाजक यह है कि, जब भी, अनजान व्यापारी ई के तहत एक बोली बेचते हैं, और सूचित व्यापारी केवल खराब होने पर एक बोली बेचते हैं। इसी तरह, हम अनुमान लगा सकते हैं

  

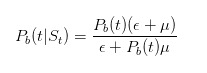
  और

  

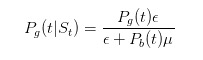
  इससे पहले कि हम आगे बढ़ें, चलो कुछ सरल परीक्षण करते हैं. हमने कहा था कि अगर हम एक बिक्री पत्र देखते हैं, तो हम अनुमान लगाते हैं कि कुछ बुरा होने की संभावना बढ़ जाती है. क्या यह सही है? हम एक बहुत ही सरल अनुमान लगा सकते हैं.

  

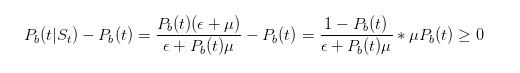
  इस प्रकार, हमारे निष्कर्ष हमारे अंतर्ज्ञान की पुष्टि करते हैं।

  अब, इस अद्यतन संभावना के साथ, हम एक उचित मूल्य की गणना कर सकते हैं, और हम इसे खरीद मूल्य के रूप में उपयोग कर सकते हैं, जो कि बाजार में है, और इसे इस तरह व्यक्त किया जा सकता है

  

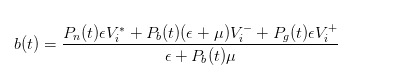
  इसी तरह के निष्कर्ष के माध्यम से, हम देख सकते हैं कि जब एक खरीद आदेश भेजा गया है, हम के रूप में एक बाजार के व्यापारी के रूप में रिपोर्ट की बिक्री मूल्य होना चाहिए

  

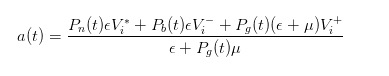
• 4 मूल्य के परिवर्तन के बाद मूल्य अंतर अभिव्यक्ति

  खरीद और बिक्री की कीमतों के लिए उपरोक्त अभिव्यक्ति काफी सहज नहीं है, हम समय टी में शेयर की उम्मीद मूल्य को शामिल कर सकते हैं अभिव्यक्ति को सरल बनाने के लिए। हम उम्मीद है कि मूल्य है

  

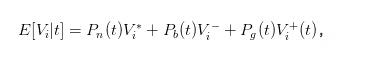
  तो हम bid और ask के expressions को

  

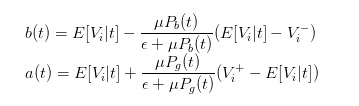
  तो हम स्पष्ट रूप से मूल्य अंतर को व्यक्त कर सकते हैं

  

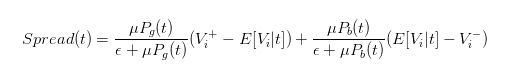
• 5 मूल्य अंतर पर व्यापारी व्यवहार का प्रभाव

  अब जब हम मूल्य अंतर के बारे में बात कर रहे हैं, तो हम विभिन्न व्यापारियों के मूल्य अंतर के प्रभाव का विश्लेषण कर सकते हैं!

  अधिक स्नीकर्स, कम अंतर. ध्यान दें कि, ε अज्ञानी व्यापारियों (हमें उन्हें स्नीकर्स कहते हैं) की पहुंच दर है, अगर वहाँ ε >> μ, हम देख सकते हैं, / upload/asset/539e0cfb1aae368277dd0e3840448b6a39abd087.png दोनों 0 की ओर बढ़ेगा, जिसका अर्थ है कि प्रसार भी शून्य की ओर बढ़ेगा।
  यदि हम एक और चरम पर जाते हैं, तो मान लीजिए कि बाजार में कोई स्नीक नहीं है, केवल एक समूह है जो जानकार व्यापारियों की तुलना में बेहतर है, तो हम दुखद रूप से पाएंगे कि हम कीमतों को / upload/asset/a38df589795e485f117660cfb019d1f2d0d50ca5.png और / upload/asset/1248ca7d3d472490982c9d0aa7b2e04b51269b18.png के रूप में देखते हैं, इसलिए जानकार व्यापारी खुद को पाते हैं कि कोई भी खरीद या बिक्री लाभदायक नहीं होगी, बाजार निश्चित रूप से मर जाएगा।

  आप देखते हैं, हम कुछ धारणाओं के आधार पर, बहुत ही सरल गणितीय अनुमानों का उपयोग करते हैं, और वास्तव में इस तरह के दिलचस्प और गहन निष्कर्ष प्राप्त कर सकते हैं, जो शायद गणितीय मॉडल का एक बड़ा आकर्षण है। इस लेख को पढ़ने के बाद, मुझे उम्मीद है कि आप भी तिलचट्टे के साथ अच्छा व्यवहार करेंगे, हम तिलचट्टे हैं जो बाजार में सामान्य लेनदेन की गारंटी देते हैं!

[1] Easley, David, et al. "Liquidity, information, and infrequently traded stocks." The Journal of Finance 51.4 (1996): 1405-1436.