डाटा आधारित प्रौद्योगिकी पर आधारित जोड़ी व्यापार

डाटा आधारित प्रौद्योगिकी पर आधारित जोड़ी व्यापार

जोड़ी व्यापार गणितीय विश्लेषण के आधार पर ट्रेडिंग रणनीतियों को तैयार करने का एक अच्छा उदाहरण है। इस लेख में, हम दिखाएंगे कि जोड़ी व्यापार रणनीतियों को बनाने और स्वचालित करने के लिए डेटा का उपयोग कैसे करें।

मूल सिद्धांत

मान लीजिए कि आपके पास कुछ संभावित संबंध रखने वाले निवेश लक्ष्य X और Y की एक जोड़ी है। उदाहरण के लिए, दो कंपनियां एक ही उत्पाद का उत्पादन करती हैं, जैसे पेप्सी कोला और कोका कोला। आप चाहते हैं कि दोनों का मूल्य अनुपात या आधार स्प्रेड (जिसे मूल्य अंतर के रूप में भी जाना जाता है) समय के साथ अपरिवर्तित रहे। हालांकि, आपूर्ति और मांग में अस्थायी परिवर्तनों के कारण, जैसे कि एक निवेश लक्ष्य का एक बड़ा खरीद / बिक्री आदेश, और कंपनियों में से एक की महत्वपूर्ण खबर की प्रतिक्रिया, दोनों जोड़े के बीच मूल्य अंतर समय-समय पर अलग हो सकता है। इस मामले में, एक निवेश वस्तु ऊपर की ओर बढ़ती है जबकि दूसरी एक-दूसरे के सापेक्ष नीचे की ओर बढ़ती है। यदि आप चाहते हैं कि यह असहमति समय के साथ सामान्य हो, तो आप ट्रेडिंग अवसर (या मध्यस्थता अवसर) पा सकते हैं। इस तरह के मध्यस्थता अवसर डिजिटल मुद्रा बाजार या घरेलू कमोडिटी वायदा बाजार में पाए जा सकते हैं, जैसे कि बीटीसी और एक कंपनी के बीच संबंध; सुरक्षित बगीचे हुए सोया अनाज, सोयाबीन तेल और सोयाबीन की संपत्ति के

जब अस्थायी मूल्य अंतर होता है, तो आप उत्कृष्ट प्रदर्शन के साथ निवेश वस्तु (बढ़ती हुई निवेश वस्तु) बेचेंगे और खराब प्रदर्शन के साथ निवेश वस्तु (घटती हुई निवेश वस्तु) खरीदेंगे। आपको यकीन है कि दोनों निवेश वस्तुओं के बीच ब्याज मार्जिन अंततः उत्कृष्ट प्रदर्शन के साथ निवेश वस्तु के गिरने या खराब प्रदर्शन के साथ निवेश वस्तु के बढ़ने या दोनों के माध्यम से गिर जाएगा। आपके लेनदेन से इन सभी समान स्थितियों में पैसा कमाया जाएगा। यदि निवेश वस्तुएं उनके बीच मूल्य अंतर को बदले बिना एक साथ ऊपर या नीचे चलती हैं, तो आप पैसा नहीं बनाते हैं या खोते हैं।

इसलिए, जोड़ी व्यापार एक बाजार तटस्थ व्यापारिक रणनीति है, जो व्यापारियों को लगभग किसी भी बाजार की स्थिति से लाभान्वित करने में सक्षम बनाता हैः ऊपर की प्रवृत्ति, नीचे की प्रवृत्ति या क्षैतिज समेकन।

अवधारणा की व्याख्या करें: दो काल्पनिक निवेश लक्ष्य

• एफएमजेड क्वांट प्लेटफॉर्म पर अपना अनुसंधान वातावरण बनाएं

सबसे पहले, सुचारू रूप से काम करने के लिए, हमें अपने अनुसंधान वातावरण का निर्माण करने की आवश्यकता है। इस लेख में, हम एफएमजेड क्वांट प्लेटफॉर्म का उपयोग करते हैं (FMZ.COM) हमारे अनुसंधान वातावरण का निर्माण करने के लिए, मुख्य रूप से सुविधाजनक और तेज़ एपीआई इंटरफ़ेस और बाद में इस मंच के अच्छी तरह से पैक किए गए डॉकर सिस्टम का उपयोग करने के लिए।

एफएमजेड क्वांट प्लेटफॉर्म के आधिकारिक नाम में इस डॉकर सिस्टम को डॉकर सिस्टम कहा जाता है।

कृपया एक डॉकर और रोबोट तैनात करने के लिए मेरे पिछले लेख देखेंःhttps://www.fmz.com/bbs-topic/9864.

जो पाठक डॉकरों को तैनात करने के लिए अपना स्वयं का क्लाउड कंप्यूटिंग सर्वर खरीदना चाहते हैं, वे इस लेख का संदर्भ ले सकते हैंःhttps://www.fmz.com/digest-topic/5711.

बाद में क्लाउड कंप्यूटिंग सर्वर और डॉकर प्रणाली को सफलतापूर्वक तैनात करने के बाद, अगला हम पाइथन के वर्तमान सबसे बड़े कलाकृतियों को स्थापित करेंगेः एनाकोंडा

इस लेख में आवश्यक सभी प्रासंगिक प्रोग्राम वातावरण (निर्भरता पुस्तकालय, संस्करण प्रबंधन, आदि) को महसूस करने के लिए, सबसे सरल तरीका एनाकोंडा का उपयोग करना है। यह एक पैक किया गया पायथन डेटा विज्ञान पारिस्थितिकी तंत्र और निर्भरता पुस्तकालय प्रबंधक है।

Anaconda की स्थापना विधि के लिए, कृपया Anaconda की आधिकारिक गाइड देखेंःhttps://www.anaconda.com/distribution/.

यह लेख पायथन वैज्ञानिक कंप्यूटिंग में दो लोकप्रिय और महत्वपूर्ण पुस्तकालयों, नम्पी और पांडा का भी उपयोग करेगा।

उपरोक्त बुनियादी कार्य मेरे पिछले लेखों का भी संदर्भ ले सकता है, जो अनाकोंडा वातावरण और नम्पी और पांडा पुस्तकालयों को स्थापित करने के तरीके का परिचय देते हैं। विवरण के लिए, कृपया देखेंःhttps://www.fmz.com/bbs-topic/9863.

इसके बाद, आइए दो काल्पनिक निवेश लक्ष्य को लागू करने के लिए कोड का उपयोग करें:

import numpy as np
import pandas as pd

import statsmodels
from statsmodels.tsa.stattools import coint
# just set the seed for the random number generator
np.random.seed(107)

import matplotlib.pyplot as plt

हाँ, हम भी उपयोग करेंगे matplotlib, पायथन में एक बहुत प्रसिद्ध चार्ट पुस्तकालय.

चलो एक काल्पनिक निवेश लक्ष्य X उत्पन्न करते हैं, और अनुकरण और सामान्य वितरण के माध्यम से अपने दैनिक रिटर्न प्लॉट करते हैं। फिर हम दैनिक X मूल्य प्राप्त करने के लिए एक संचयी योग प्रदर्शन करते हैं।

# Generate daily returns
Xreturns = np.random.normal(0, 1, 100) 
# sum them and shift all the prices up
X = pd.Series(np.cumsum(
    Xreturns), name='X') 
    + 50
X.plot(figsize=(15,7))
plt.show()

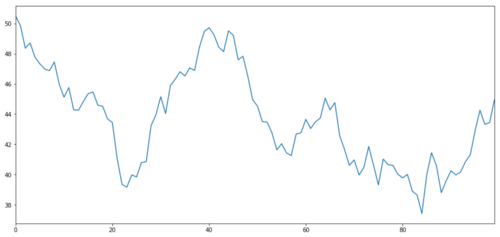
निवेश वस्तु के एक्स को सामान्य वितरण के माध्यम से उसके दैनिक रिटर्न को प्लॉट करने के लिए सिमुलेट किया जाता है

अब हम Y उत्पन्न करते हैं, जो X के साथ दृढ़ता से एकीकृत है, इसलिए Y की कीमत X के परिवर्तन के समान होनी चाहिए। हम इसे X ले कर मॉडल करते हैं, इसे ऊपर ले जाते हैं और सामान्य वितरण से निकाले गए कुछ यादृच्छिक शोर जोड़ते हैं।

noise = np.random.normal(0, 1, 100)
Y = X + 5 + noise
Y.name = 'Y'
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.show()

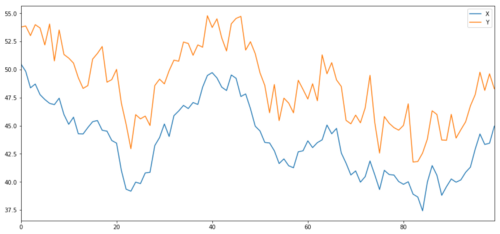
सहसंयोजन निवेश वस्तु का एक्स और वाई

सहसंयोजन

सहसंयोजन सहसंयोजन के समान है, जिसका अर्थ है कि दो डेटा श्रृंखलाओं के बीच अनुपात औसत मूल्य के करीब बदल जाएगा। वाई और एक्स श्रृंखला निम्नानुसार हैः

Y = X + e

जहां एक निरंतर अनुपात है और e शोर है।

दो समय श्रृंखलाओं के बीच व्यापार करने वाले जोड़े के लिए, समय के साथ अनुपात का अपेक्षित मूल्य औसत मूल्य के लिए अभिसरित होना चाहिए, अर्थात, उन्हें सह-संयोजित किया जाना चाहिए। हमने ऊपर जो समय श्रृंखला बनाई है वह सह-संयोजित है। हम अब उनके बीच अनुपात को ग्राफ करेंगे ताकि हम देख सकें कि यह कैसा दिखता है।

(Y/X).plot(figsize=(15,7)) 
plt.axhline((Y/X).mean(), color='red', linestyle='--') 
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()

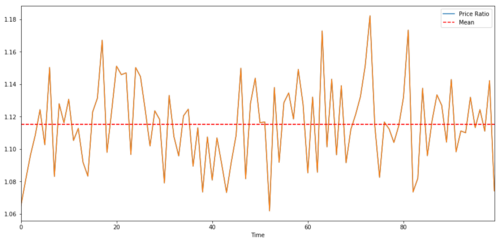
दो एकीकृत निवेश लक्ष्य मूल्यों के बीच अनुपात और औसत मूल्य

सहसंयोजन परीक्षण

एक सुविधाजनक परीक्षण विधि का उपयोग करना है statsmodels.tsa.stattools. हम एक बहुत कम पी मूल्य देखेंगे, क्योंकि हमने दो डेटा श्रृंखला कृत्रिम रूप से बनाई है जो यथासंभव सह-एकीकृत हैं।

# compute the p-value of the cointegration test
# will inform us as to whether the ratio between the 2 timeseries is stationary
# around its mean
score, pvalue, _ = coint(X,Y)
print pvalue

परिणाम हैः 1.81864477307e-17

नोटः सहसंबंध और सहसंयोजन

सहसंबंध और सहसंयोजन, यद्यपि सिद्धांत में समान हैं, समान नहीं हैं। आइए प्रासंगिक लेकिन सहसंयोजित डेटा श्रृंखलाओं के उदाहरणों को देखें और इसके विपरीत। सबसे पहले, आइए हम अभी उत्पन्न श्रृंखला के सहसंबंध की जांच करें।

X.corr(Y)

परिणाम हैः 0.951

जैसा कि हम उम्मीद करते हैं, यह बहुत अधिक है। लेकिन दो संबंधित लेकिन सह-संयोजित नहीं श्रृंखला के बारे में क्या? एक सरल उदाहरण दो विचलित डेटा की एक श्रृंखला है।

ret1 = np.random.normal(1, 1, 100)
ret2 = np.random.normal(2, 1, 100)

s1 = pd.Series( np.cumsum(ret1), name='X')
s2 = pd.Series( np.cumsum(ret2), name='Y')

pd.concat([s1, s2], axis=1 ).plot(figsize=(15,7))
plt.show()
print 'Correlation: ' + str(X_diverging.corr(Y_diverging))
score, pvalue, _ = coint(X_diverging,Y_diverging)
print 'Cointegration test p-value: ' + str(pvalue)

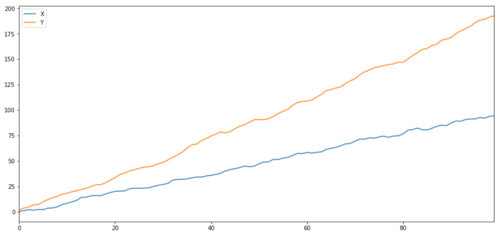
दो संबंधित श्रृंखलाएँ (एक साथ एकीकृत नहीं)

सहसंबंध गुणांक: 0.998 सहसंयोजन परीक्षण का पी मानः 0.258

सहसंयोजन के सरल उदाहरण सामान्य वितरण अनुक्रम और वर्ग तरंगें हैं।

Y2 = pd.Series(np.random.normal(0, 1, 800), name='Y2') + 20
Y3 = Y2.copy()
Y3[0:100] = 30

Y3[100:200] = 10
Y3[200:300] = 30
Y3[300:400] = 10
Y3[400:500] = 30
Y3[500:600] = 10
Y3[600:700] = 30
Y3[700:800] = 10
Y2.plot(figsize=(15,7))
Y3.plot()
plt.ylim([0, 40])
plt.show()
# correlation is nearly zero
print 'Correlation: ' + str(Y2.corr(Y3))
score, pvalue, _ = coint(Y2,Y3)
print 'Cointegration test p-value: ' + str(pvalue)

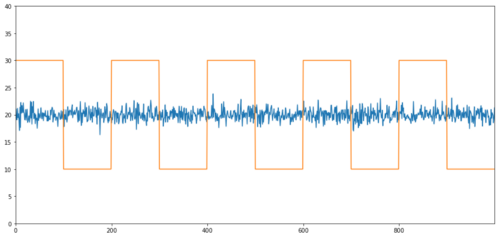
सहसंबंधः 0.007546 सहसंयोजन परीक्षण का पी मानः 0.0

सहसंबंध बहुत कम है, लेकिन पी मूल्य सही सह-संयोजन दिखाता है!

युग्म व्यापार कैसे किया जाता है?

चूंकि दो सह-एकीकृत समय श्रृंखलाएं (जैसे ऊपर X और Y) एक-दूसरे के सामने हैं और एक-दूसरे से विचलित होती हैं, कभी-कभी आधार स्प्रेड उच्च या निम्न होता है। हम एक निवेश वस्तु खरीदकर और दूसरे को बेचकर जोड़ी व्यापार करते हैं। इस तरह, यदि दो निवेश लक्ष्य एक साथ गिरते हैं या बढ़ते हैं, तो हम न तो पैसा कमाएंगे और न ही पैसा खोएंगे, यानी हम बाजार में तटस्थ हैं।

उपरोक्त के लिए वापस, X और Y में Y = X + e, ताकि अनुपात (Y / X) अपने औसत मूल्य के चारों ओर चले। हम औसत मूल्य प्रतिगमन के अनुपात के माध्यम से पैसा बनाते हैं। ऐसा करने के लिए, हम उस मामले पर ध्यान देंगे जहां X और Y दूर हैं, अर्थात का मूल्य बहुत अधिक या बहुत कम हैः

• लंबे अनुपात में जाना: यह तब होता है जब अनुपात बहुत छोटा होता है और हम उम्मीद करते हैं कि यह बढ़ेगा। उपरोक्त उदाहरण में, हम लंबी Y और छोटी X जाकर स्थिति खोलते हैं।

• शॉर्ट रेशियोः यह तब होता है जब रेशियो बहुत बड़ा होता है और हम उम्मीद करते हैं कि यह कम हो जाएगा। उपरोक्त उदाहरण में, हम शॉर्ट Y और लॉन्ग X जाकर स्थिति खोलते हैं।

कृपया ध्यान दें कि हमारे पास हमेशा हेज पोजीशन होती हैः यदि ट्रेडिंग सब्जेक्ट लॉस वैल्यू खरीदता है, तो शॉर्ट पोजीशन पैसा कमाएगी, और इसके विपरीत, इसलिए हम समग्र बाजार प्रवृत्ति से प्रतिरक्षित हैं।

यदि व्यापार वस्तु के एक्स और वाई एक दूसरे के सापेक्ष चलते हैं, तो हम पैसा कमाएंगे या पैसा खो देंगे।

समान व्यवहार के साथ व्यापार वस्तुओं को खोजने के लिए डेटा का उपयोग करें

ऐसा करने का सबसे अच्छा तरीका यह है कि आप उस ट्रेडिंग विषय से शुरू करें जिसके बारे में आपको संदेह है कि यह सह-संयोजन हो सकता है और एक सांख्यिकीय परीक्षण करें। यदि आप सभी ट्रेडिंग जोड़े पर सांख्यिकीय परीक्षण करते हैं, तो आप इसके शिकार हो जाएंगेकई तुलनात्मक पूर्वाग्रह.

कई तुलनात्मक पूर्वाग्रहकई परीक्षणों को चलाने के दौरान गलत तरीके से महत्वपूर्ण पी मान उत्पन्न करने की संभावना को संदर्भित करता है, क्योंकि हमें बड़ी संख्या में परीक्षण चलाने की आवश्यकता है। यदि हम यादृच्छिक डेटा पर 100 परीक्षण चलाते हैं, तो हमें 0.5 से कम 5 पी मान देखना चाहिए। यदि आप सह-संयोजन के लिए n व्यापारिक लक्ष्यों की तुलना करना चाहते हैं, तो आप n (n-1) / 2 तुलना करेंगे, और आपको कई गलत पी मान दिखाई देंगे, जो आपके परीक्षण नमूनों की वृद्धि के साथ बढ़ेंगे। इस स्थिति से बचने के लिए, कुछ व्यापारिक जोड़े चुनें और आपके पास यह निर्धारित करने का कारण है कि वे सह-संयोजन हो सकते हैं, और फिर उन्हें अलग से परीक्षण करें। इससे बहुत कम होगाकई तुलनात्मक पूर्वाग्रह.

इसलिए, चलो कुछ व्यापारिक लक्ष्यों को खोजने की कोशिश करते हैं जो सह-एकीकरण दिखाते हैं। आइए एक उदाहरण के रूप में एस एंड पी 500 सूचकांक में बड़े अमेरिकी प्रौद्योगिकी शेयरों की एक टोकरी लेते हैं। ये व्यापारिक लक्ष्य समान बाजार खंडों में संचालित होते हैं और सह-एकीकरण मूल्य होते हैं। हम व्यापार वस्तुओं की सूची को स्कैन करते हैं और सभी जोड़े के बीच सह-एकीकरण का परीक्षण करते हैं।

लौटाया गया सह-समीकरण परीक्षण स्कोर मैट्रिक्स, पी-मूल्य मैट्रिक्स और सभी जोड़े जिनकी पी-मूल्य 0.05 से कम है।यह विधि कई तुलना पूर्वाग्रह के लिए प्रवण है, इसलिए वास्तव में, उन्हें एक दूसरा सत्यापन करने की आवश्यकता है।इस लेख में, हमारी व्याख्या की सुविधा के लिए, हम उदाहरण में इस बिंदु को नजरअंदाज करने का विकल्प चुनते हैं।

def find_cointegrated_pairs(data):
    n = data.shape[1]
    score_matrix = np.zeros((n, n))
    pvalue_matrix = np.ones((n, n))
    keys = data.keys()
    pairs = []
    for i in range(n):
        for j in range(i+1, n):
            S1 = data[keys[i]]
            S2 = data[keys[j]]
            result = coint(S1, S2)
            score = result[0]
            pvalue = result[1]
            score_matrix[i, j] = score
            pvalue_matrix[i, j] = pvalue
            if pvalue < 0.02:
                pairs.append((keys[i], keys[j]))
    return score_matrix, pvalue_matrix, pairs

नोटः हमने बाजार बेंचमार्क (एसपीएक्स) को डेटा में शामिल किया है - बाजार ने कई ट्रेडिंग ऑब्जेक्ट्स के प्रवाह को चलाया है। आमतौर पर आपको दो ट्रेडिंग ऑब्जेक्ट मिल सकते हैं जो सह-एकीकृत प्रतीत होते हैं; लेकिन वास्तव में, वे एक दूसरे के साथ नहीं, बल्कि बाजार के साथ सह-एकीकृत होते हैं। इसे एक भ्रमित करने वाला चर कहा जाता है। आपको मिलने वाले किसी भी संबंध में बाजार भागीदारी की जांच करना महत्वपूर्ण है।

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2007/12/01'
endDateStr = '2017/12/01'
cachedFolderName = 'yahooData/'
dataSetId = 'testPairsTrading'
instrumentIds = ['SPY','AAPL','ADBE','SYMC','EBAY','MSFT','QCOM',
                 'HPQ','JNPR','AMD','IBM']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
data = ds.getBookDataByFeature()['Adj Close']
data.head(3)

अब चलो सहसंयोजित व्यापारिक जोड़े खोजने के लिए हमारी विधि का उपयोग करने की कोशिश करते हैं।

# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds, 
                yticklabels=instrumentIds, cmap=’RdYlGn_r’, 
                mask = (pvalues >= 0.98))
plt.show()
print pairs

[('ADBE', 'MSFT')]

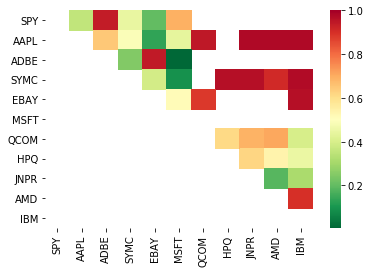
ऐसा लगता है कि ADBE और MSFT कोएन्टीग्रेट कर रहे हैं. चलो कीमत पर एक नज़र डालते हैं यह सुनिश्चित करने के लिए कि यह वास्तव में समझ में आता है.

S1 = data['ADBE']
S2 = data['MSFT']
score, pvalue, _ = coint(S1, S2)
print(pvalue)
ratios = S1 / S2
ratios.plot()
plt.axhline(ratios.mean())
plt.legend([' Ratio'])
plt.show()

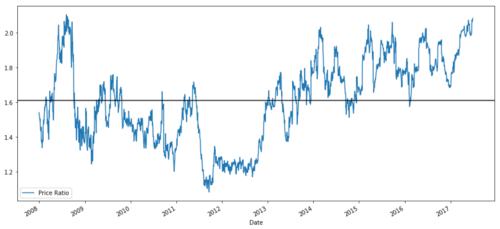
एमएसएफटी और एडीबीई के बीच 2008 से 2017 तक के मूल्य अनुपात ग्राफ

यह अनुपात एक स्थिर औसत की तरह दिखता है। पूर्ण अनुपात सांख्यिकीय रूप से उपयोगी नहीं हैं। इसे Z स्कोर के रूप में मानकीकृत करके हमारे संकेतों को मानकीकृत करना अधिक उपयोगी है। Z स्कोर को परिभाषित किया गया हैः

Z स्कोर (मूल्य) = (मूल्य औसत) / मानक विचलन

चेतावनी

वास्तव में, हम आमतौर पर डेटा को इस आधार पर विस्तारित करने की कोशिश करते हैं कि डेटा सामान्य रूप से वितरित है। हालांकि, कई वित्तीय डेटा सामान्य रूप से वितरित नहीं होते हैं, इसलिए हमें सांख्यिकी उत्पन्न करते समय सामान्यता या किसी विशिष्ट वितरण को केवल मानने के लिए बहुत सावधान रहना चाहिए। अनुपातों का वास्तविक वितरण एक वसा-पूंछ प्रभाव हो सकता है, और वे डेटा जो चरम होने की प्रवृत्ति रखते हैं हमारे मॉडल को भ्रमित करेंगे और भारी नुकसान का कारण बनेंगे।

def zscore(series):
    return (series - series.mean()) / np.std(series)

zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()

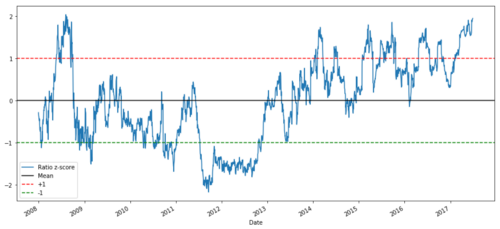
एमएसएफटी और एडीबीई के बीच 2008 से 2017 के बीच मूल्य अनुपात

अब औसत मूल्य के निकट अनुपात के आंदोलन का निरीक्षण करना आसान है, लेकिन कभी-कभी औसत मूल्य से बड़ा अंतर होना आसान होता है। हम इसका लाभ उठा सकते हैं।

अब जब हमने जोड़ी ट्रेडिंग रणनीति के बुनियादी ज्ञान पर चर्चा की है, और ऐतिहासिक मूल्य के आधार पर संयुक्त एकीकरण का विषय निर्धारित किया है, तो आइए एक ट्रेडिंग सिग्नल विकसित करने का प्रयास करें। सबसे पहले, आइए डेटा प्रौद्योगिकी का उपयोग करके ट्रेडिंग सिग्नल विकसित करने के चरणों की समीक्षा करेंः

• विश्वसनीय डेटा एकत्र करना और डेटा को साफ करना;

• ट्रेडिंग सिग्नल/लॉजिक की पहचान करने के लिए डेटा से फ़ंक्शन बनाएं;

• फ़ंक्शन चलती औसत या मूल्य डेटा, अधिक जटिल संकेतों के सहसंबंध या अनुपात हो सकते हैं - इनका संयोजन करके नए फ़ंक्शन बनाए जा सकते हैं;

• इन कार्यों का उपयोग ट्रेडिंग सिग्नल उत्पन्न करने के लिए करें, यानी, कौन से सिग्नल खरीद, बिक्री या शॉर्ट पोजीशन पर नजर रखने के लिए हैं।

सौभाग्य से, हमारे पास FMZ क्वांट प्लेटफॉर्म है (fmz.com), जिसने हमारे लिए उपरोक्त चार पहलुओं को पूरा किया है, जो रणनीति विकासकों के लिए एक बड़ा आशीर्वाद है। हम अपनी ऊर्जा और समय को रणनीति तर्क के डिजाइन और कार्यों के विस्तार के लिए समर्पित कर सकते हैं।

एफएमजेड क्वांट प्लेटफॉर्म में, विभिन्न मुख्यधारा के एक्सचेंजों के लिए कैप्सुलेटेड इंटरफेस हैं। हमें क्या करने की आवश्यकता है इन एपीआई इंटरफेस को कॉल करना है। अंतर्निहित कार्यान्वयन तर्क का बाकी हिस्सा एक पेशेवर टीम द्वारा समाप्त हो गया है।

तर्क को पूरा करने और इस लेख में सिद्धांत को समझाने के लिए, हम इन अंतर्निहित तर्क को विस्तार से प्रस्तुत करेंगे। हालांकि, वास्तविक संचालन में, पाठक उपरोक्त चार पहलुओं को पूरा करने के लिए सीधे एफएमजेड क्वांट एपीआई इंटरफ़ेस को कॉल कर सकते हैं।

चलो शुरू करते हैंः

चरण 1: अपना प्रश्न पूछें

यहाँ, हम एक संकेत बनाने की कोशिश हमें बताओ कि क्या अनुपात खरीदने या अगले क्षण में बेचने के लिए होगा, अर्थात्, हमारे भविष्यवाणी चर वाईः

Y = अनुपात खरीद (1) या बिक्री (-1) है

Y(t)= Sign(Ratio(t+1) Ratio(t))

कृपया ध्यान दें कि हमें वास्तविक लेनदेन लक्ष्य मूल्य, या अनुपात के वास्तविक मूल्य की भविष्यवाणी करने की आवश्यकता नहीं है (हालांकि हम कर सकते हैं), लेकिन केवल अगले चरण में अनुपात की दिशा।

चरण 2: विश्वसनीय और सटीक डेटा एकत्र करें

एफएमजेड क्वांट आपका दोस्त है! आपको केवल लेनदेन ऑब्जेक्ट को विनिमय करने और उपयोग करने के लिए डेटा स्रोत निर्दिष्ट करने की आवश्यकता है, और यह आवश्यक डेटा निकालेगा और लाभांश और लेनदेन ऑब्जेक्ट विभाजन के लिए इसे साफ करेगा। इसलिए यहां डेटा बहुत साफ है।

पिछले 10 वर्षों के व्यापारिक दिनों (लगभग 2500 डेटा बिंदु) पर, हमने याहू फाइनेंस का उपयोग करके निम्नलिखित डेटा प्राप्त कियाः उद्घाटन मूल्य, समापन मूल्य, उच्चतम मूल्य, निम्नतम मूल्य और व्यापारिक मात्रा।

चरण 3: डेटा को विभाजित करें

मॉडल की सटीकता का परीक्षण करने में इस बहुत महत्वपूर्ण कदम को मत भूलिए। हम प्रशिक्षण/प्रमाणन/परीक्षण विभाजन के लिए निम्नलिखित डेटा का उपयोग कर रहे हैं।

• प्रशिक्षण 7 वर्ष ~ 70%

• परीक्षण ~ 3 वर्ष 30%

ratios = data['ADBE'] / data['MSFT']
print(len(ratios))
train = ratios[:1762]
test = ratios[1762:]

आदर्श रूप से, हमें सत्यापन सेट भी बनाना चाहिए, लेकिन हम अभी ऐसा नहीं करेंगे।

चरण 4: फीचर इंजीनियरिंग

संबंधित कार्य क्या हो सकते हैं? हम अनुपात परिवर्तन की दिशा की भविष्यवाणी करना चाहते हैं। हमने देखा है कि हमारे दो व्यापारिक लक्ष्य सह-संयोजित हैं, इसलिए यह अनुपात औसत मूल्य पर स्थानांतरित होने और लौटने की प्रवृत्ति रखता है। ऐसा लगता है कि हमारी विशेषताओं को औसत अनुपात के कुछ उपाय होने चाहिए, और वर्तमान मूल्य और औसत मूल्य के बीच का अंतर हमारे व्यापार संकेत उत्पन्न कर सकता है।

हम निम्नलिखित कार्यों का उपयोग करते हैंः

• 60 दिन का चलती औसत अनुपात: चलती औसत का मापन;

• पांच दिवसीय चलती औसत अनुपातः औसत के वर्तमान मूल्य का माप;

• 60 दिन का मानक विचलन;

• Z स्कोर: (5d MA - 60d MA) / 60d SD.

ratios_mavg5 = train.rolling(window=5,
                               center=False).mean()
ratios_mavg60 = train.rolling(window=60,
                               center=False).mean()
std_60 = train.rolling(window=60,
                        center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()

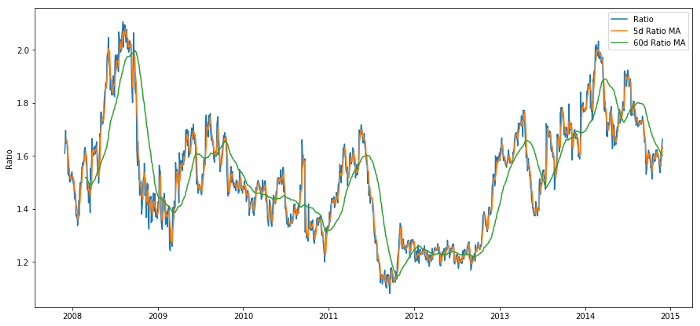
60d और 5d एमए के बीच मूल्य अनुपात

plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()

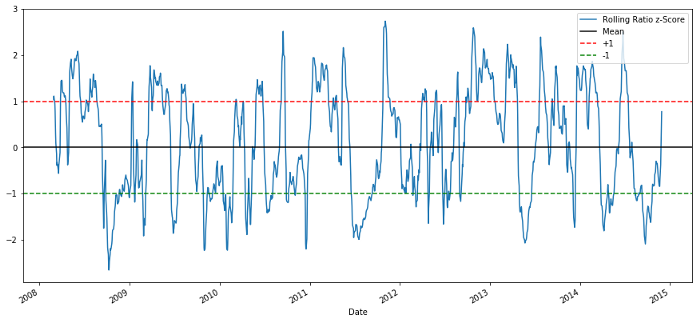
60-5 Z स्कोर मूल्य अनुपात

चलती औसत मूल्य का Z स्कोर अनुपात के औसत मूल्य प्रतिगमन गुण को बाहर लाता है!

चरण 5: मॉडल का चयन

चलो एक बहुत ही सरल मॉडल के साथ शुरू करते हैं। z स्कोर चार्ट को देखते हुए, हम देख सकते हैं कि यदि z स्कोर बहुत अधिक या बहुत कम है, तो यह वापस आ जाएगा। चलो बहुत अधिक और बहुत कम परिभाषित करने के लिए हमारे थ्रेशोल्ड के रूप में +1/- 1 का उपयोग करते हैं और फिर हम निम्नलिखित मॉडल का उपयोग ट्रेडिंग संकेत उत्पन्न करने के लिए कर सकते हैं:

• जब z -1.0 से नीचे है, अनुपात खरीदना है (1), क्योंकि हम उम्मीद करते हैं कि z 0 पर लौटने के लिए, इसलिए अनुपात बढ़ जाता है;

• जब z 1.0 से ऊपर होता है, तो अनुपात बेचा जाता है (- 1), क्योंकि हम उम्मीद करते हैं कि z 0 पर लौटता है, इसलिए अनुपात कम हो जाता है।

चरण 6: प्रशिक्षण, सत्यापन और अनुकूलन

अंत में, आइए वास्तविक डेटा पर हमारे मॉडल के वास्तविक प्रभाव पर एक नज़र डालें। आइए वास्तविक अनुपात पर इस संकेत के प्रदर्शन पर एक नज़र डालेंः

# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color=’g’, linestyle=’None’, marker=’^’)
sell[60:].plot(color=’r’, linestyle=’None’, marker=’^’)
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend([‘Ratio’, ‘Buy Signal’, ‘Sell Signal’])
plt.show()

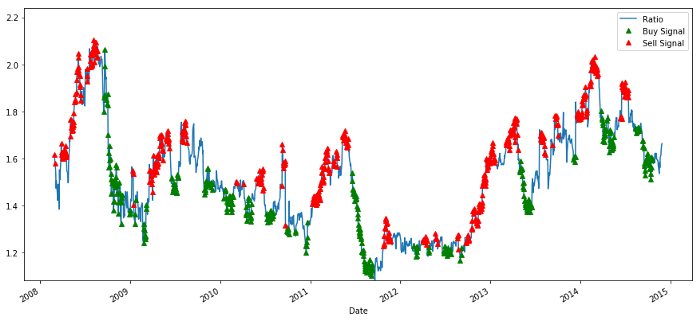
खरीद और बिक्री मूल्य अनुपात संकेत

संकेत उचित प्रतीत होता है. हम बेचते हैं जब यह उच्च या बढ़ रहा है (लाल डॉट्स) और इसे वापस खरीदते हैं जब यह कम है (हरी डॉट्स) और घट रहा है. हमारे लेनदेन के वास्तविक विषय के लिए इसका क्या मतलब है? आइए देखेंः

# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1 = data['ADBE'].iloc[:1762]
S2 = data['MSFT'].iloc[:1762]
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2 
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['ADBE','MSFT', 'Buy Signal', 'Sell Signal'])
plt.show()

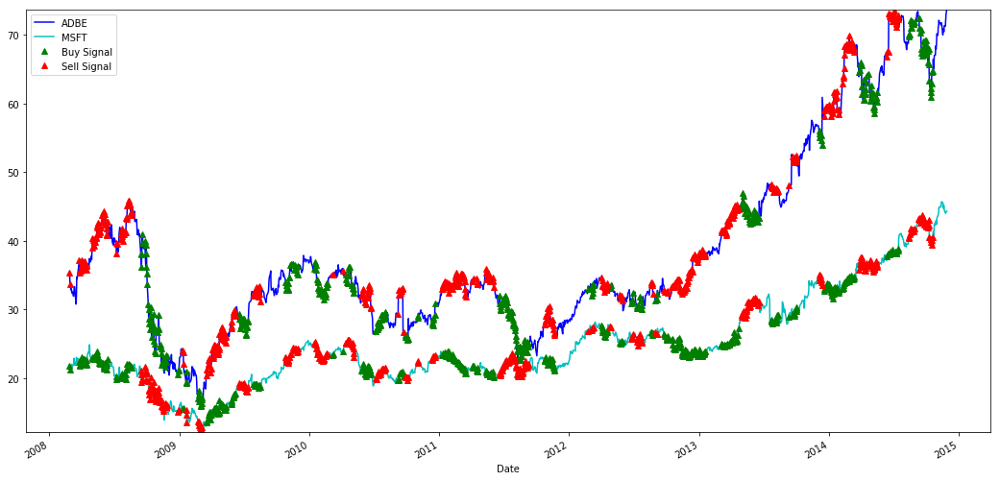
एमएसएफटी और एडीबीई शेयरों की खरीद और बिक्री के संकेत

कृपया ध्यान दें कि हम कभी-कभी छोटे पैरों पर, कभी-कभी लम्बे पैरों पर, और कभी-कभी दोनों पर कैसे लाभ कमाते हैं।

हम प्रशिक्षण डेटा के संकेत से संतुष्ट हैं। आइए देखें कि यह संकेत किस प्रकार का लाभ उत्पन्न कर सकता है। जब अनुपात कम होता है, तो हम एक सरल बैक-टेस्टर कर सकते हैं, एक अनुपात खरीद सकते हैं (1 ADBE स्टॉक खरीदें और अनुपात x MSFT स्टॉक बेचें), और एक अनुपात बेचें (1 ADBE स्टॉक बेचें और अनुपात x MSFT स्टॉक खरीदें) जब यह उच्च हो, और इन अनुपातों के PnL लेनदेन की गणना करें।

# Trade using a simple strategy
def trade(S1, S2, window1, window2):
    
    # If window length is 0, algorithm doesn't make sense, so exit
    if (window1 == 0) or (window2 == 0):
        return 0
    
    # Compute rolling mean and rolling standard deviation
    ratios = S1/S2
    ma1 = ratios.rolling(window=window1,
                               center=False).mean()
    ma2 = ratios.rolling(window=window2,
                               center=False).mean()
    std = ratios.rolling(window=window2,
                        center=False).std()
    zscore = (ma1 - ma2)/std
    
    # Simulate trading
    # Start with no money and no positions
    money = 0
    countS1 = 0
    countS2 = 0
    for i in range(len(ratios)):
        # Sell short if the z-score is > 1
        if zscore[i] > 1:
            money += S1[i] - S2[i] * ratios[i]
            countS1 -= 1
            countS2 += ratios[i]
            print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
        # Buy long if the z-score is < 1
        elif zscore[i] < -1:
            money -= S1[i] - S2[i] * ratios[i]
            countS1 += 1
            countS2 -= ratios[i]
            print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
        # Clear positions if the z-score between -.5 and .5
        elif abs(zscore[i]) < 0.75:
            money += S1[i] * countS1 + S2[i] * countS2
            countS1 = 0
            countS2 = 0
            print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
            
            
    return money
trade(data['ADBE'].iloc[:1763], data['MSFT'].iloc[:1763], 60, 5)

परिणाम है: 1783.375

तो यह रणनीति लाभदायक लगती है! अब, हम आगे चल औसत समय खिड़की को बदलकर अनुकूलित कर सकते हैं, खरीद / बिक्री और बंद पदों की सीमाओं को बदलकर, और सत्यापन डेटा के प्रदर्शन में सुधार की जांच करके।

हम 1/-1 की भविष्यवाणी करने के लिए अधिक जटिल मॉडल, जैसे लॉजिस्टिक प्रतिगमन और एसवीएम का भी प्रयास कर सकते हैं।

अब, चलो इस मॉडल को आगे बढ़ाते हैं, जो हमें लाता हैः

चरण 7: परीक्षण डेटा का बैकटेस्ट करें

यहां भी, एफएमजेड क्वांट प्लेटफॉर्म ऐतिहासिक वातावरण को सही ढंग से पुनः पेश करने के लिए एक उच्च प्रदर्शन वाले क्यूपीएस / टीपीएस बैकटेस्टिंग इंजन को अपनाता है, सामान्य मात्रात्मक बैकटेस्टिंग जाल को समाप्त करता है, और समय में रणनीतियों की कमियों की खोज करता है, ताकि वास्तविक बॉट निवेश में बेहतर मदद मिल सके।

सिद्धांत को समझाने के लिए, यह लेख अभी भी अंतर्निहित तर्क दिखाने का विकल्प चुनता है। व्यावहारिक अनुप्रयोग में, हम पाठकों को एफएमजेड क्वांट प्लेटफॉर्म का उपयोग करने की सलाह देते हैं। समय बचाने के अलावा, गलती सहिष्णुता दर में सुधार करना महत्वपूर्ण है।

बैकटेस्टिंग सरल है. हम परीक्षण डेटा के पीएनएल को देखने के लिए उपरोक्त फ़ंक्शन का उपयोग कर सकते हैं.

trade(data['ADBE'].iloc[1762:], data['MSFT'].iloc[1762:], 60, 5)

परिणाम हैः 5262.868

मॉडल ने बहुत अच्छा काम किया! यह हमारा पहला सरल जोड़ा जोड़ी व्यापार मॉडल बन गया।

ओवरफिटिंग से बचें

चर्चा को समाप्त करने से पहले, मैं विशेष रूप से ओवरफिटिंग पर चर्चा करना चाहूंगा। ओवरफिटिंग ट्रेडिंग रणनीतियों में सबसे खतरनाक जाल है। ओवरफिटिंग एल्गोरिथ्म बैकटेस्ट में बहुत अच्छा प्रदर्शन कर सकता है लेकिन नए अदृश्य डेटा पर विफल हो सकता है - जिसका अर्थ है कि यह वास्तव में डेटा का कोई रुझान प्रकट नहीं करता है और इसकी कोई वास्तविक भविष्यवाणी क्षमता नहीं है। आइए एक सरल उदाहरण दें।

हमारे मॉडल में, हम समय खिड़की की लंबाई का अनुमान लगाने और अनुकूलित करने के लिए रोलिंग मापदंडों का उपयोग करते हैं। हम बस सभी संभावनाओं पर पुनरावृत्ति करने का निर्णय ले सकते हैं, एक उचित समय खिड़की की लंबाई, और हमारे मॉडल के सर्वोत्तम प्रदर्शन के अनुसार समय की लंबाई चुन सकते हैं। चलो एक सरल लूप लिखते हैं प्रशिक्षण डेटा के पीएनएल के अनुसार समय खिड़की की लंबाई को स्कोर करने के लिए और सबसे अच्छा लूप ढूंढें।

# Find the window length 0-254 
# that gives the highest returns using this strategy
length_scores = [trade(data['ADBE'].iloc[:1762], 
                data['MSFT'].iloc[:1762], l, 5) 
                for l in range(255)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)

('Best window length:', 40)

अब हम परीक्षण डेटा पर मॉडल के प्रदर्शन की जांच करते हैं, और हम पाते हैं कि इस समय खिड़की की लंबाई इष्टतम से दूर है! यह इसलिए है क्योंकि हमारे मूल विकल्प स्पष्ट रूप से नमूने डेटा से अधिक फिट है।

# Find the returns for test data
# using what we think is the best window length
length_scores2 = [trade(data['ADBE'].iloc[1762:], 
                  data['MSFT'].iloc[1762:],l,5) 
                  for l in range(255)]
print (best_length, 'day window:', length_scores2[best_length])
# Find the best window length based on this dataset, 
# and the returns using this window length
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])

(40, 'day window:', 1252233.1395)
(15, 'day window:', 1449116.4522)

यह स्पष्ट है कि हमारे लिए उपयुक्त नमूना डेटा भविष्य में हमेशा अच्छे परिणाम नहीं देगा। केवल परीक्षण के लिए, आइए दो डेटा सेटों से गणना किए गए लंबाई स्कोर को ग्राफ करेंः

plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()

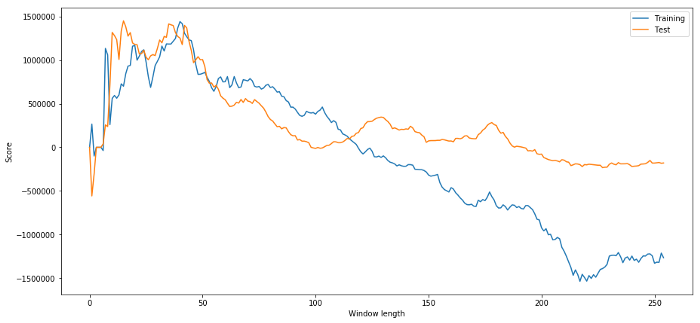
हम देख सकते हैं कि 20 से 50 के बीच कुछ भी समय खिड़कियों के लिए एक अच्छा विकल्प है।

ओवरफिट से बचने के लिए, हम समय खिड़की की लंबाई का चयन करने के लिए आर्थिक तर्क या एल्गोरिथ्म की प्रकृति का उपयोग कर सकते हैं। हम कैलमैन फ़िल्टर का भी उपयोग कर सकते हैं, जिसके लिए हमें लंबाई निर्दिष्ट करने की आवश्यकता नहीं है; इस दृष्टिकोण का वर्णन बाद में एक अन्य लेख में किया जाएगा।

अगला कदम

इस लेख में, हम व्यापार रणनीतियों के विकास की प्रक्रिया का प्रदर्शन करने के लिए कुछ सरल परिचयात्मक तरीकों का प्रस्ताव करते हैं। व्यवहार में, अधिक जटिल सांख्यिकी का उपयोग किया जाना चाहिए। आप निम्नलिखित विकल्पों पर विचार कर सकते हैंः

• हर्स्ट एक्सपोनेंट;

• अर्नस्टीन-उलेनबेक प्रक्रिया से अनुमानित औसत प्रतिगमन का आधा जीवन;

• काल्मन फ़िल्टर।

संबंधित

अधिक