बेयज़ - संभावना के रहस्य का पता लगाना, निर्णय लेने के पीछे गणितीय बुद्धि का पता लगाना

बायेसियन सांख्यिकी गणित के क्षेत्र में एक शक्तिशाली अनुशासन है, जिसमें वित्त, चिकित्सा अनुसंधान और सूचना प्रौद्योगिकी सहित कई क्षेत्रों में व्यापक अनुप्रयोग हैं। यह हमें नई पिछली मान्यताओं को प्राप्त करने के लिए साक्ष्य के साथ पहले की मान्यताओं को जोड़ने की अनुमति देता है, जिससे हम अधिक बुद्धिमान निर्णय ले सकते हैं।

इस लेख में, हम इस क्षेत्र के संस्थापकों में से कुछ मुख्य गणितज्ञों का संक्षिप्त परिचय देंगे।

बेयज़ से पहले बेजियन सांख्यिकी को बेहतर ढंग से समझने के लिए हमें 18वीं शताब्दी में वापस जाना होगा और गणितज्ञ डी मोइवर और उनके पेपर 'द डक्ट्रिन ऑफ चांस' का उल्लेख करना होगा।

अपने पेपर में, डी मोइवर ने अपने युग में संभावनाओं और जुआ से संबंधित कई समस्याओं को हल किया। जैसा कि आप जानते होंगे, इन समस्याओं में से एक के उनके समाधान ने सामान्य वितरण की उत्पत्ति का कारण बना, लेकिन यह एक और कहानी है।

उनके पेपर में सबसे सरल प्रश्नों में से एक था:

एक निष्पक्ष सिक्का लगातार तीन बार फेंके जाने पर तीन सिर मिलने की संभावना क्या है?

The Doctrine of Chances में वर्णित समस्याओं को पढ़ते हुए, आप देख सकते हैं कि अधिकांश एक धारणा के साथ शुरू करते हैं जिससे वे दी गई घटनाओं के लिए संभावनाओं की गणना करते हैं। उदाहरण के लिए, उपरोक्त प्रश्न में एक धारणा है जो सिक्के को निष्पक्ष मानती है; इसलिए, एक टॉस के दौरान सिर प्राप्त करने की संभावना 0.5 है।

इसे आज गणितीय शब्दों में इस प्रकार व्यक्त किया जाएगा:

सूत्र

𝑃(𝑋|𝜃)

हालांकि, क्या होगा अगर हम नहीं जानते कि सिक्का निष्पक्ष है या नहीं?𝜃 ?

थॉमस बेयज़ और रिचर्ड प्राइस

लगभग पचास वर्ष बाद, 1763 में, रॉयल सोसाइटी ऑफ लंदन के दार्शनिक लेनदेन में ए सॉल्यूशन टू द प्रॉब्लम्स इन द डक्ट्रिन ऑफ चांस नामक एक पेपर प्रकाशित किया गया।

इस दस्तावेज़ के पहले कुछ पन्नों में गणितज्ञ रिचर्ड प्राइस द्वारा लिखा गया एक टुकड़ा है जो उनकी मृत्यु से कई साल पहले उनके दोस्त थॉमस बेयज़ द्वारा लिखे गए एक पेपर का सारांश देता है। अपने परिचय में, प्राइस ने थॉमस बेयज़ द्वारा की गई कुछ महत्वपूर्ण खोजों की व्याख्या की, जिनका उल्लेख डी मोइवर के संभव का सिद्धांत में नहीं किया गया था।

वास्तव में, उन्होंने एक विशिष्ट समस्या का उल्लेख कियाः

एक अज्ञात घटना की सफलताओं और असफलताओं की संख्या को देखते हुए, किसी भी दो नामित डिग्री के बीच इसकी संभावना का पता लगाएं.

दूसरे शब्दों में, एक घटना का निरीक्षण करने के बाद हम निर्धारित क्या संभावना है कि एक अज्ञात पैरामीटर हैθदो डिग्री के बीच गिर जाता है. यह वास्तव में इतिहास में सांख्यिकीय निष्कर्ष से संबंधित पहली समस्याओं में से एक है और यह शब्द विपरीत संभावना को जन्म दिया. गणितीय शब्दों मेंः

सूत्र

𝑃( 𝜃 | 𝑋）

यह है कि हम आज Bayes प्रमेय के पीछे वितरण कहते हैं।

बिना कारण और प्रभाव के कारण

इन दो वरिष्ठ मंत्रियों के शोध के पीछे की प्रेरणाओं को समझते हुए,थॉमस बेयज़औररिचर्ड प्राइस, वास्तव में काफी दिलचस्प है. लेकिन ऐसा करने के लिए, हम अस्थायी रूप से सांख्यिकी के बारे में कुछ ज्ञान को अलग करने की जरूरत है.

हम 18वीं शताब्दी में हैं जब गणितज्ञों के लिए संभावना एक तेजी से दिलचस्प क्षेत्र बन रही है। डी मोइवर या बर्नौली जैसे गणितज्ञों ने पहले ही दिखाया है कि कुछ घटनाएं एक निश्चित डिग्री के साथ होती हैं यादृच्छिकता लेकिन अभी भी निश्चित नियमों द्वारा शासित हैं। उदाहरण के लिए, यदि आप एक पासा कई बार फेंकते हैं, तो एक छठा समय यह छह पर उतर जाएगा। यह ऐसा है जैसे कि एक छिपा हुआ नियम है जो भाग्य की संभावनाओं को निर्धारित करता है।

अब कल्पना कीजिए कि आप इस काल में रहने वाले एक गणितज्ञ और भक्त हैं। आप इस छिपे हुए नियम और ईश्वर के बीच के संबंध को समझने में रुचि रख सकते हैं।

यह वास्तव में स्वयं बेयज़ और प्राइस द्वारा पूछा गया प्रश्न था। उन्हें उम्मीद थी कि उनका समाधान सीधे यह साबित करने के लिए लागू होगा कि दुनिया को ज्ञान और बुद्धि का परिणाम होना चाहिए; इसलिए परम कारण के रूप में ईश्वर के अस्तित्व के लिए सबूत प्रदान करना - यानी कारण के बिना कारण।

लैप्लेस

आश्चर्यजनक रूप से, लगभग दो साल बाद 1774 में, थॉमस बेयज़ के पेपर को पढ़े बिना, फ्रांसीसी गणितज्ञ लैप्लास ने एक पेपर लिखा जिसका शीर्षक था घटनाओं की संभावना द्वारा घटनाओं के कारणों पर, जो विपरीत संभावना समस्याओं के बारे में है। पहले पृष्ठ पर, आप मुख्य सिद्धांत पढ़ सकते हैंः

यदि किसी घटना का कारण n अलग-अलग कारण हो सकते हैं, तो इन कारणों के बीच के अनुपात घटना को दी गई संभावनाएं इन कारणों को दी गई घटनाओं की संभावनाओं के बराबर होती हैं; और प्रत्येक कारण की अस्तित्व संभावना इस घटना को दी गई कारणों की संभावना को इन कारणों में से प्रत्येक को दी गई घटनाओं की कुल संभावनाओं से विभाजित करने के बराबर होती है।

यह आज हम बेयज़ प्रमेय के रूप में जानते हैंः

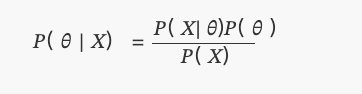
कहाँP(θ)एक समान वितरण है।

सिक्का प्रयोग

हम पायथन और PyMC लाइब्रेरी का उपयोग करके वर्तमान में Bayesian सांख्यिकी लाएंगे, और एक सरल प्रयोग करेंगे।

मान लीजिए कि एक दोस्त आपको एक सिक्का देता है और पूछता है कि क्या आपको लगता है कि यह एक उचित सिक्का है। क्योंकि वह जल्दी में है, वह आपको बताता है कि आप केवल 10 बार सिक्का फेंक सकते हैं। जैसा कि आप देख सकते हैं, एक अज्ञात पैरामीटर हैpइस समस्या में, जो सिक्के फेंकने में सिर पाने की संभावना है, और हम सबसे अधिक संभावना मूल्य का अनुमान लगाना चाहते हैंp.

(नोटः हम नहीं कह रहे हैं कि पैरामीटरpएक यादृच्छिक चर है, बल्कि यह है कि यह पैरामीटर तय है; हम जानना चाहते हैं कि यह सबसे अधिक संभावना है।

इस समस्या पर अलग-अलग विचार रखने के लिए, हम इसे दो अलग-अलग पूर्व मान्यताओं के तहत हल करेंगे:

• 1. आपके पास सिक्के की निष्पक्षता के बारे में कोई पूर्व जानकारी नहीं है, इसलिए आप एक समान संभावना को असाइन करते हैंpइस मामले में, हम एक गैर सूचनात्मक पूर्व कहा जाता है का उपयोग करेंगे क्योंकि आपने अपने विश्वासों के लिए कोई जानकारी नहीं जोड़ी है।
• 2. अपने अनुभव से, आप जानते हैं कि भले ही एक सिक्का अन्यायपूर्ण हो सकता है, यह इसे बेहद अन्यायपूर्ण बनाने के लिए मुश्किल है। इसलिए आप पैरामीटर मानते हैंp0.3 से कम या 0.7 से अधिक होने की संभावना नहीं है। इस मामले में, हम एक सूचनात्मक पूर्व का उपयोग करेंगे।

इन दोनों परिदृश्यों के लिए, हमारे पूर्व विश्वास निम्नानुसार होंगे:

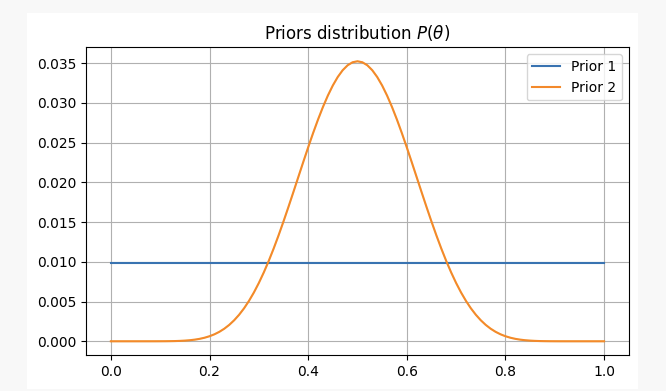
एक सिक्का 10 बार फेंकने के बाद, आप दो बार सिर मिल गया है. इस सबूत के साथ, जहां हम अपने पैरामीटर खोजने के लिए संभावना हैp?

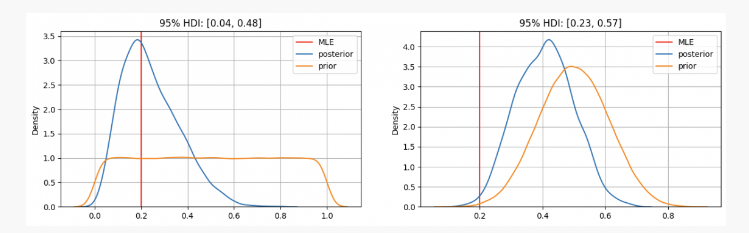
जैसा कि आप देख सकते हैं, पहले मामले में, पैरामीटर के हमारे पूर्व वितरणpअधिकतम संभावना अनुमान (एमएलई) पर केंद्रित हैp=0.2, जो कि आवृत्ति विद्यालय द्वारा उपयोग की जाने वाली विधि के समान है। वास्तविक अज्ञात पैरामीटर 0.04 और 0.48 के बीच 95% विश्वास अंतराल के भीतर होगा।

दूसरी ओर, ऐसे मामलों में जहां उच्च विश्वास है कि पैरामीटरp0.3 और 0.7 के बीच होना चाहिए, हम देख सकते हैं कि पिछली वितरण के आसपास 0.4 है, जो हमारे एमएलई हमें देता है की तुलना में बहुत अधिक है। इस मामले में सही अज्ञात पैरामीटर 0.23 और 0.57 के बीच एक 95% आत्मविश्वास अंतराल के भीतर होगा।

इसलिए, पहले परिदृश्य में आप निश्चितता के साथ अपने मित्र को बताएंगे कि यह सिक्का निष्पक्ष नहीं है लेकिन दूसरी स्थिति में आप कहेंगे कि यह अनिश्चित है कि यह निष्पक्ष है या नहीं।

जैसा कि आप देख सकते हैं कि समान साक्ष्य (दस में से दो सिर) के साथ सामना करने पर भी, विभिन्न पूर्व मान्यताओं के तहत परिणाम बहुत भिन्न हो सकते हैं; पारंपरिक तरीकों पर बेजियन सांख्यिकी का एक लाभ यहां हैः वैज्ञानिक पद्धति की तरह यह हमें नए अवलोकनों और साक्ष्य के साथ संयोजन करके अपनी मान्यताओं को अपडेट करने की अनुमति देता है।

अंत

आज के लेख में हमने बेजियन सांख्यिकी की उत्पत्ति और इसके मुख्य योगदानकर्ताओं को देखा। बाद में सांख्यिकी के इस क्षेत्र में कई अन्य महत्वपूर्ण योगदानकर्ता (जेफ्रीज, कॉक्स, शैनन आदि) आए हैं, जोquantdare.com.