लंबी-छोटी पोजीशनों के लिए संतुलित इक्विटी रणनीतियों को व्यवस्थित रूप से संरेखित करना

लंबी-छोटी पोजीशनों के लिए संतुलित इक्विटी रणनीतियों को व्यवस्थित रूप से संरेखित करना

पिछले लेख में (https://www.fmz.com/bbs-topic/9862), हमने जोड़ी व्यापार रणनीतियों का परिचय दिया और दिखाया कि डेटा और गणितीय विश्लेषण का उपयोग करके व्यापार रणनीतियों को कैसे बनाया और स्वचालित किया जाए।

लंबी-लघु स्थिति संतुलित इक्विटी रणनीति व्यापार वस्तुओं की टोकरी पर लागू जोड़ी व्यापार रणनीति का एक प्राकृतिक विस्तार है। यह विशेष रूप से कई किस्मों और परस्पर संबंधों वाले व्यापार बाजारों के लिए उपयुक्त है, जैसे कि डिजिटल मुद्रा बाजार और कमोडिटी वायदा बाजार।

मूल सिद्धांत

लंबी शॉर्ट पोजीशन संतुलित इक्विटी रणनीति ट्रेडिंग लक्ष्यों की एक टोकरी को एक साथ लंबी और छोटी करना है। जोड़ी ट्रेडिंग की तरह, यह निर्धारित करता है कि कौन सा निवेश लक्ष्य सस्ता है और कौन सा निवेश लक्ष्य महंगा है। अंतर यह है कि लंबी शॉर्ट पोजीशन संतुलित इक्विटी रणनीति स्टॉक चयन पूल में सभी निवेश लक्ष्यों को व्यवस्थित करेगी ताकि यह निर्धारित किया जा सके कि कौन से निवेश लक्ष्य अपेक्षाकृत सस्ते या महंगे हैं। फिर, यह रैंकिंग के आधार पर शीर्ष एन निवेश लक्ष्यों को लंबा करेगा, और नीचे एन निवेश लक्ष्यों को समान राशि में छोटा करेगा (लंबी पदों का कुल मूल्य = लघु पदों का कुल मूल्य) ।

क्या आपको याद है कि हमने जोड़ा ट्रेडिंग को बाजार तटस्थ रणनीति कहा था? लंबी शॉर्ट पोजीशन संतुलित इक्विटी रणनीति के लिए भी यही सच है, क्योंकि लंबी और छोटी पोजीशन की समान मात्रा यह सुनिश्चित करती है कि रणनीति बाजार तटस्थ रहेगी (बाजार के उतार-चढ़ाव से प्रभावित नहीं होती है) । रणनीति भी सांख्यिकीय रूप से मजबूत है; निवेश लक्ष्यों को रैंक करके और लंबी पोजीशन को पकड़कर, आप अपनी रैंकिंग मॉडल पर कई बार पोजीशन खोल सकते हैं, न कि केवल एक बार जोखिम खोलने की स्थिति। आप पूरी तरह से अपनी रैंकिंग योजना की गुणवत्ता पर दांव लगा रहे हैं।

रैंकिंग योजना क्या है?

रैंकिंग योजना एक मॉडल है जो प्रत्येक निवेश विषय को अपेक्षित प्रदर्शन के अनुसार प्राथमिकता दे सकती है। कारक मूल्य कारक, तकनीकी संकेतक, मूल्य निर्धारण मॉडल या उपरोक्त सभी कारकों का संयोजन हो सकते हैं। उदाहरण के लिए, आप ट्रेंड ट्रैकिंग निवेश लक्ष्यों की एक श्रृंखला को रैंक करने के लिए गति संकेतक का उपयोग कर सकते हैंः यह उम्मीद की जाती है कि उच्चतम गति के साथ निवेश लक्ष्य अच्छा प्रदर्शन करना जारी रखेंगे और उच्चतम रैंकिंग प्राप्त करेंगे; सबसे कम गति के साथ निवेश वस्तु का सबसे खराब प्रदर्शन और सबसे कम रिटर्न है।

इस रणनीति की सफलता लगभग पूरी तरह से उपयोग की गई रैंकिंग योजना पर निर्भर करती है, अर्थात, आपकी रैंकिंग योजना उच्च प्रदर्शन निवेश लक्ष्य को कम प्रदर्शन निवेश लक्ष्य से अलग कर सकती है, ताकि लंबी और छोटी स्थिति निवेश लक्ष्यों की रणनीति के रिटर्न को बेहतर ढंग से महसूस किया जा सके। इसलिए, रैंकिंग योजना विकसित करना बहुत महत्वपूर्ण है।

रैंकिंग योजना कैसे बनाई जाए?

एक बार जब हम रैंकिंग योजना निर्धारित कर लेते हैं, तो हम इससे लाभ कमाने की उम्मीद करते हैं। हम शीर्ष निवेश लक्ष्यों को लंबा करने और निचले निवेश लक्ष्यों को छोटा करने के लिए समान मात्रा में पूंजी का निवेश करके ऐसा करते हैं। यह सुनिश्चित करता है कि रणनीति केवल रैंकिंग की गुणवत्ता के अनुपात में लाभ कमाएगी, और यह बाजार तटस्थ होगी।

मान लीजिए कि आप सभी निवेश लक्ष्यों m को रैंक कर रहे हैं, और आपके पास निवेश के लिए n डॉलर हैं, और आप कुल 2p (जहां m>2p) पदों को रखना चाहते हैं। यदि निवेश ऑब्जेक्ट रैंकिंग रैंक 1 सबसे खराब प्रदर्शन करने की उम्मीद है, तो निवेश ऑब्जेक्ट रैंकिंग m सबसे अच्छा प्रदर्शन करने की उम्मीद हैः

• आप निवेश वस्तुओं को क्रमबद्ध करते हैंः 1,...,p स्थिति, 2/2p USD के निवेश लक्ष्य को छोटा करें।

• आप निवेश वस्तुओं को क्रमबद्ध करते हैंः एम-पी,...,एम स्थिति, एन / 2 पी यूएसडी के निवेश लक्ष्य को लंबा करें।

नोटः क्योंकि मूल्य उतार-चढ़ाव के कारण निवेश विषय वस्तु की कीमत हमेशा समान रूप से n/2p को विभाजित नहीं करेगी, और कुछ निवेश विषय वस्तुओं को पूर्णांक के साथ खरीदा जाना चाहिए, कुछ गलत एल्गोरिदम होंगे, जो इस संख्या के जितना संभव हो उतना करीब होना चाहिए। n = 100000 और p = 500 चलाने वाली रणनीतियों के लिए, हम देखते हैं किः

n/2p = 100000/1000 = 100

यह 100 से अधिक मूल्य वाले स्कोर के लिए एक बड़ी समस्या पैदा करेगा (जैसे कि कमोडिटी वायदा बाजार), क्योंकि आप एक अंश मूल्य के साथ स्थिति नहीं खोल सकते हैं (यह समस्या डिजिटल मुद्रा बाजारों में मौजूद नहीं है) । हम अंश मूल्य लेनदेन को कम करके या पूंजी बढ़ाकर इस स्थिति को कम करते हैं।

आइए एक काल्पनिक उदाहरण लेते हैं।

• एफएमजेड क्वांट प्लेटफॉर्म पर अपना अनुसंधान वातावरण बनाएं

सबसे पहले, सुचारू रूप से काम करने के लिए, हमें अपने अनुसंधान वातावरण का निर्माण करने की आवश्यकता है। इस लेख में, हम एफएमजेड क्वांट प्लेटफॉर्म का उपयोग करते हैं (FMZ.COM) हमारे अनुसंधान वातावरण का निर्माण करने के लिए, मुख्य रूप से सुविधाजनक और तेज़ एपीआई इंटरफ़ेस और बाद में इस मंच के अच्छी तरह से पैक किए गए डॉकर सिस्टम का उपयोग करने के लिए।

एफएमजेड क्वांट प्लेटफॉर्म के आधिकारिक नाम में इस डॉकर सिस्टम को डॉकर सिस्टम कहा जाता है।

कृपया एक डॉकर और रोबोट तैनात करने के लिए मेरे पिछले लेख देखेंःhttps://www.fmz.com/bbs-topic/9864.

जो पाठक डॉकरों को तैनात करने के लिए अपना स्वयं का क्लाउड कंप्यूटिंग सर्वर खरीदना चाहते हैं, वे इस लेख का संदर्भ ले सकते हैंःhttps://www.fmz.com/digest-topic/5711.

बाद में क्लाउड कंप्यूटिंग सर्वर और डॉकर प्रणाली को सफलतापूर्वक तैनात करने के बाद, अगला हम पाइथन के वर्तमान सबसे बड़े कलाकृतियों को स्थापित करेंगेः एनाकोंडा

इस लेख में आवश्यक सभी प्रासंगिक प्रोग्राम वातावरण (निर्भरता पुस्तकालय, संस्करण प्रबंधन, आदि) को महसूस करने के लिए, सबसे सरल तरीका एनाकोंडा का उपयोग करना है। यह एक पैक किया गया पायथन डेटा विज्ञान पारिस्थितिकी तंत्र और निर्भरता पुस्तकालय प्रबंधक है।

Anaconda की स्थापना विधि के लिए, कृपया Anaconda की आधिकारिक गाइड देखेंःhttps://www.anaconda.com/distribution/.

यह लेख पायथन वैज्ञानिक कंप्यूटिंग में दो लोकप्रिय और महत्वपूर्ण पुस्तकालयों, नम्पी और पांडा का भी उपयोग करेगा।

उपरोक्त बुनियादी कार्य मेरे पिछले लेखों का भी संदर्भ ले सकता है, जो अनाकोंडा वातावरण और नम्पी और पांडा पुस्तकालयों को स्थापित करने के तरीके का परिचय देते हैं। विवरण के लिए, कृपया देखेंःhttps://www.fmz.com/digest-topic/9863.

हम यादृच्छिक निवेश लक्ष्य उत्पन्न करते हैं और उन्हें रैंक करने के लिए यादृच्छिक कारकों। चलो मान लें कि हमारे भविष्य के रिटर्न वास्तव में इन कारक मूल्यों पर निर्भर करते हैं।

import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
## PROBLEM SETUP ##
# Generate stocks and a random factor value for them
stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)
# Generate future returns for these are dependent on our factor values
future_returns = current_factor_values + np.random.normal(0, 1, 10000)
# Put both the factor values and returns into one dataframe
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

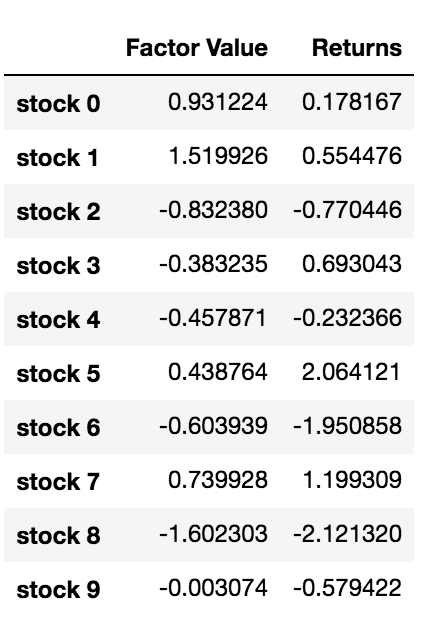
अब जब हमारे पास कारक मूल्य और रिटर्न है, तो हम देख सकते हैं कि क्या होता है यदि हम कारक मूल्यों के आधार पर निवेश लक्ष्यों को रैंक करते हैं और फिर लंबी और छोटी स्थिति खोलते हैं।

# Rank stocks
ranked_data = data.sort_values('Factor Value')
# Compute the returns of each basket with a basket size 500, so total (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)
for i in range(number_of_baskets):
    start = i * 500
    end = i * 500 + 500 
    basket_returns[i] = ranked_data[start:end]['Returns'].mean()
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

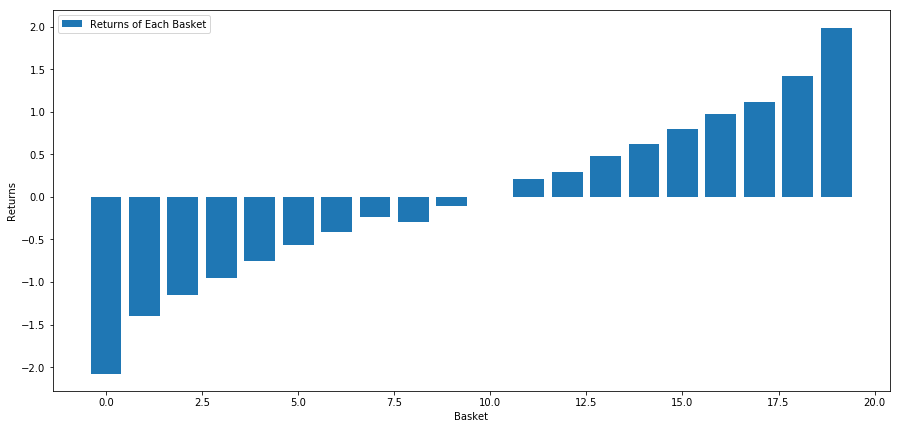
हमारी रणनीति निवेश लक्ष्य पूल की पहली रैंक वाली टोकरी को लंबा करना है; दसवीं रैंक वाली टोकरी से कम जाना है। इस रणनीति के लिए रिटर्न हैंः

basket_returns[number_of_baskets-1] - basket_returns[0]

परिणाम हैः 4.172

हमारे रैंकिंग मॉडल पर पैसा लगाएं ताकि यह उच्च प्रदर्शन वाले निवेश लक्ष्यों को निम्न प्रदर्शन वाले निवेश लक्ष्यों से अलग कर सके।

इस लेख के शेष भाग में, हम रैंकिंग योजना का मूल्यांकन करने के तरीके पर चर्चा करेंगे। रैंकिंग आधारित आर्बिटेज का लाभ यह है कि यह बाजार अव्यवस्था से प्रभावित नहीं होता है, इसके बजाय बाजार अव्यवस्था का उपयोग किया जा सकता है।

आइए एक वास्तविक दुनिया के उदाहरण पर विचार करें।

हमने एस एंड पी 500 सूचकांक में विभिन्न उद्योगों के 32 शेयरों के लिए डेटा लोड किया और उन्हें रैंक करने की कोशिश की।

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
                'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
                'HD','LOW','KO','LLY','MCD','MET','NEM',
                'PEP','PG','M','SWN','T','TGT',
                'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
price = 'adjClose'

आइए रैंकिंग के आधार के रूप में एक महीने की अवधि के लिए मानकीकृत गति संकेतक का उपयोग करें।

## Define normalized momentum
def momentum(dataDf, period):
    return dataDf.sub(dataDf.shift(period), fill_value=0) / dataDf.iloc[-1]
## Load relevant prices in a dataframe
data = ds.getBookDataByFeature()['Adj Close']
#Let's load momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

अब हम अपने स्टॉक के व्यवहार का विश्लेषण करेंगे और देखेंगे कि हमारे स्टॉक हमारे द्वारा चुने गए रैंकिंग कारक में बाजार में कैसे काम करते हैं।

आंकड़ों का विश्लेषण करें

स्टॉक व्यवहार

आइए देखें कि हमारे चयनित स्टॉक की टोकरी हमारे रैंकिंग मॉडल में कैसे प्रदर्शन करती है। ऐसा करने के लिए, आइए हम सभी स्टॉक के लिए साप्ताहिक फॉरवर्ड रिटर्न की गणना करें। फिर हम प्रत्येक स्टॉक के 1 सप्ताह के फॉरवर्ड रिटर्न और पिछले 30 दिनों के गति के बीच संबंध देख सकते हैं। सकारात्मक सहसंबंध दिखाने वाले स्टॉक ट्रेंड फॉलोअर्स हैं, जबकि नकारात्मक सहसंबंध दिखाने वाले स्टॉक औसत उलट हैं।

# Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = True)
# Calculate correlations between momentum and returns
correlations = pd.DataFrame(index = returns.columns, columns = ['Scores', 'pvalues'])
mscores = mscores[mscores.index.isin(returns.index)]
for i in correlations.index:
    score, pvalue = stats.spearmanr(mscores[i], returns[i])
    correlations[‘pvalues’].loc[i] = pvalue
    correlations[‘Scores’].loc[i] = score
correlations.dropna(inplace = True)
correlations.sort_values('Scores', inplace=True)
l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations['Scores'])
plt.xlabel('Stocks')
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.legend(['Correlation over All Data'])
plt.ylabel('Correlation between %s day Momentum Scores and %s-day forward returns by Stock'%(day,forward_return_day));
plt.show()

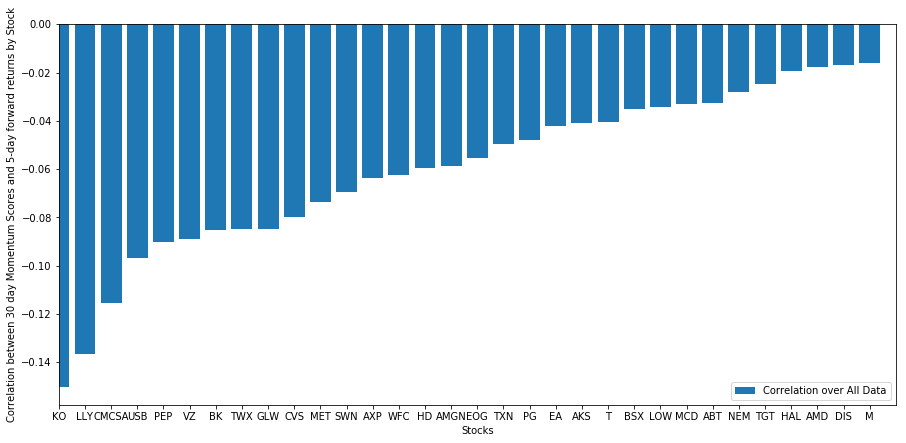
हमारे सभी शेयरों में एक निश्चित हद तक औसत प्रतिगमन होता है! (जाहिर है, हमने जो ब्रह्मांड चुना है वह इस तरह काम करता है) यह हमें बताता है कि यदि स्टॉक गति विश्लेषण में शीर्ष स्थान पर हैं, तो हमें उम्मीद करनी चाहिए कि वे अगले सप्ताह खराब प्रदर्शन करेंगे।

गति विश्लेषण के स्कोर और रिटर्न के बीच संबंध

इसके बाद, हमें हमारे रैंकिंग स्कोर और बाजार के समग्र फोरवर्ड रिटर्न के बीच संबंध देखने की आवश्यकता है, अर्थात, भविष्यवाणी की गई रिटर्न दर और हमारे रैंकिंग कारक के बीच संबंध। क्या उच्च संबंध स्तर कम सापेक्ष रिटर्न की भविष्यवाणी कर सकता है, या इसके विपरीत?

इस उद्देश्य के लिए, हम सभी शेयरों के 30-दिवसीय गति और 1-सप्ताह के फोरवर्ड रिटर्न के बीच दैनिक सहसंबंध की गणना करते हैं।

correl_scores = pd.DataFrame(index = returns.index.intersection(mscores.index), columns = ['Scores', 'pvalues'])
for i in correl_scores.index:
    score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
    correl_scores['pvalues'].loc[i] = pvalue
    correl_scores['Scores'].loc[i] = score
correl_scores.dropna(inplace = True)
l = correl_scores.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correl_scores['Scores'])
plt.hlines(np.mean(correl_scores['Scores']), 1,l+1, colors='r', linestyles='dashed')
plt.xlabel('Day')
plt.xlim((1, l+1))
plt.legend(['Mean Correlation over All Data', 'Daily Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

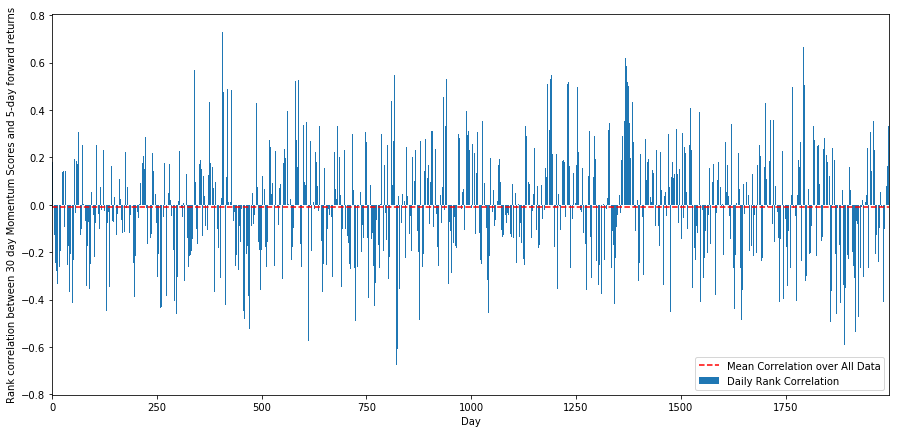
दैनिक सहसंबंध एक बहुत ही जटिल लेकिन बहुत ही मामूली सहसंबंध दिखाते हैं (जो कि उम्मीद की जाती है क्योंकि हमने कहा कि सभी स्टॉक औसत पर लौटेंगे) । हमें 1 महीने के फोरवर्ड रिटर्न के औसत मासिक सहसंबंध को भी देखना होगा।

monthly_mean_correl =correl_scores['Scores'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colors='r', linestyles='dashed')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

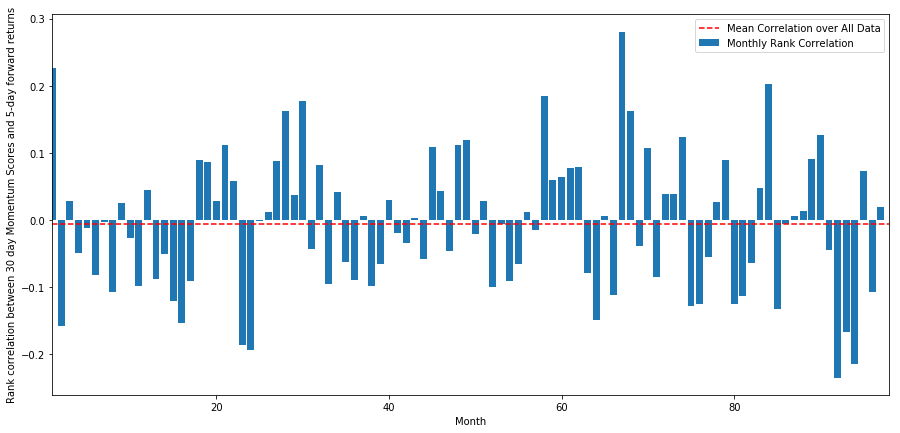
हम देख सकते हैं कि औसत सहसंबंध फिर से थोड़ा नकारात्मक है, लेकिन यह भी हर महीने बहुत बदल जाता है।

शेयरों की टोकरी पर औसत रिटर्न

हमने अपनी रैंकिंग से लिए गए स्टॉक की टोकरी पर रिटर्न की गणना की है। यदि हम सभी स्टॉक को रैंक करते हैं और उन्हें एनएन समूहों में विभाजित करते हैं, तो प्रत्येक समूह का औसत रिटर्न क्या है?

पहला कदम एक फ़ंक्शन बनाना है जो प्रत्येक बास्केट के औसत रिटर्न और रैंकिंग कारक को हर महीने देगा।

def compute_basket_returns(factor, forward_returns, number_of_baskets, index):
data = pd.concat([factor.loc[index],forward_returns.loc[index]], axis=1)
    # Rank the equities on the factor values
    data.columns = ['Factor Value', 'Forward Returns']
    data.sort_values('Factor Value', inplace=True)
    # How many equities per basket
    equities_per_basket = np.floor(len(data.index) / number_of_baskets)
basket_returns = np.zeros(number_of_baskets)
# Compute the returns of each basket
    for i in range(number_of_baskets):
        start = i * equities_per_basket
        if i == number_of_baskets - 1:
            # Handle having a few extra in the last basket when our number of equities doesn't divide well
            end = len(data.index) - 1
        else:
            end = i * equities_per_basket + equities_per_basket
        # Actually compute the mean returns for each basket
        #s = data.index.iloc[start]
        #e = data.index.iloc[end]
        basket_returns[i] = data.iloc[int(start):int(end)]['Forward Returns'].mean()
        
    return basket_returns

जब हम इस स्कोर के आधार पर शेयरों को रैंक करते हैं, तो हम प्रत्येक टोकरी के औसत रिटर्न की गणना करते हैं। इससे हमें उनके संबंध को लंबे समय तक समझने की अनुमति मिलनी चाहिए।

number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(float).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = True)
for m in forward_returns.index.intersection(resampled_scores.index):
    basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
    mean_basket_returns += basket_returns
mean_basket_returns /= l    
print(mean_basket_returns)
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

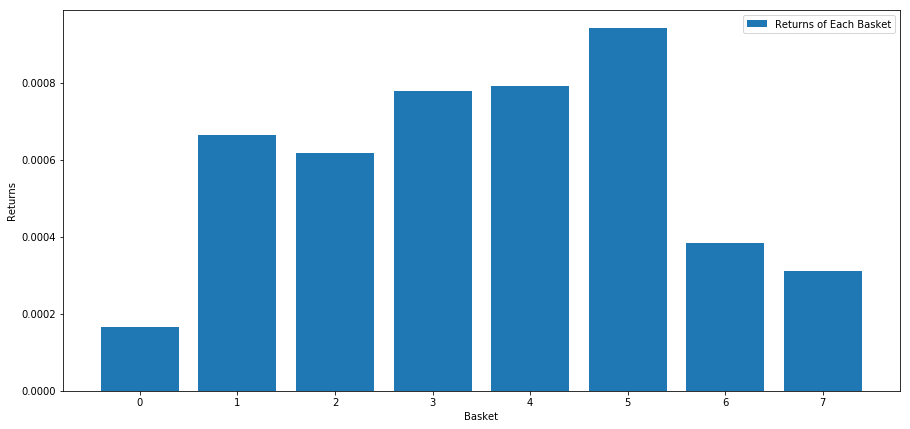
ऐसा लगता है कि हम उच्च प्रदर्शन करने वालों को निम्न प्रदर्शन करने वालों से अलग कर सकते हैं।

मार्जिन (आधार) की स्थिरता

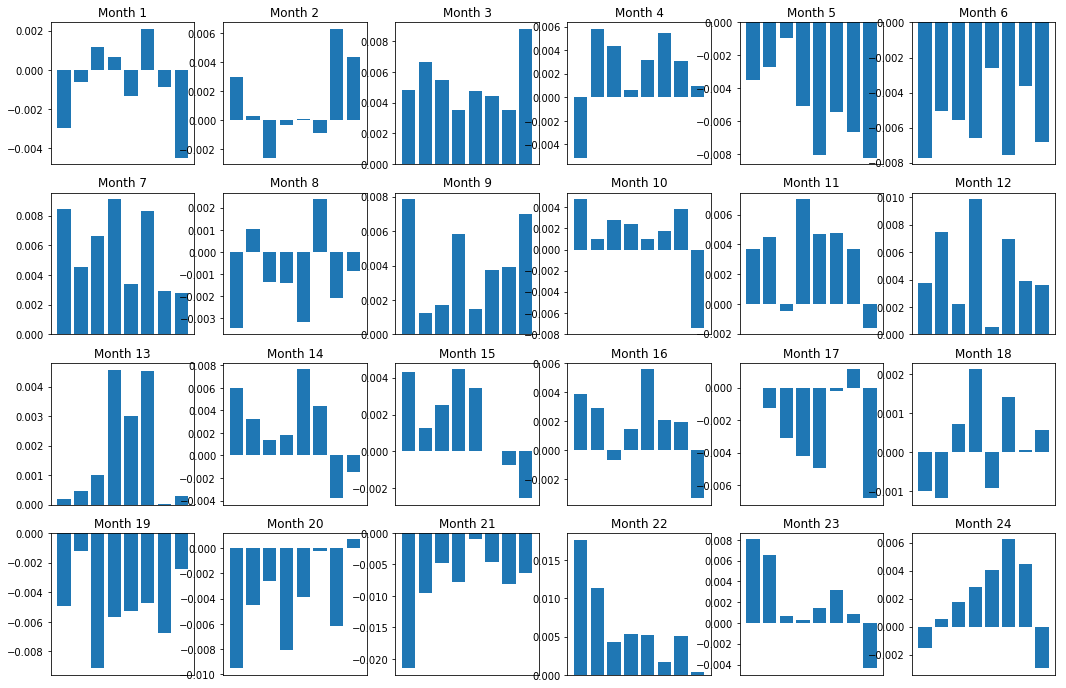
बेशक, ये केवल औसत संबंध हैं। यह समझने के लिए कि संबंध कितना सुसंगत है और क्या हम व्यापार करने के इच्छुक हैं, हमें समय के साथ इसके प्रति अपना दृष्टिकोण और दृष्टिकोण बदलना चाहिए। इसके बाद, हम पिछले दो वर्षों के लिए उनके मासिक ब्याज मार्जिन (आधार) को देखेंगे। हम अधिक परिवर्तन देख सकते हैं और यह निर्धारित करने के लिए आगे विश्लेषण कर सकते हैं कि क्या यह गति स्कोर व्यापार किया जा सकता है।

total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
    temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[month]]
    temp_scores = resampled_scores.loc[monthly_index[month-1]:monthly_index[month]]
    for m in temp_returns.index.intersection(temp_scores.index):
        basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
        mean_basket_returns += basket_returns
    
    strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
    
    mean_basket_returns /= temp_returns.index.intersection(temp_scores.index).size
    
    r = int(np.floor((month-1) / 6))
    c = (month-1) % 6
    axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
    axarr[r, c].xaxis.set_visible(False)
    axarr[r, c].set_title('Month ' + str(month))
plt.show()

plt.figure(figsize=(15,7))
plt.plot(strategy_returns)
plt.ylabel('Returns')
plt.xlabel('Month')
plt.plot(strategy_returns.cumsum())
plt.legend(['Monthly Strategy Returns', 'Cumulative Strategy Returns'])
plt.show()

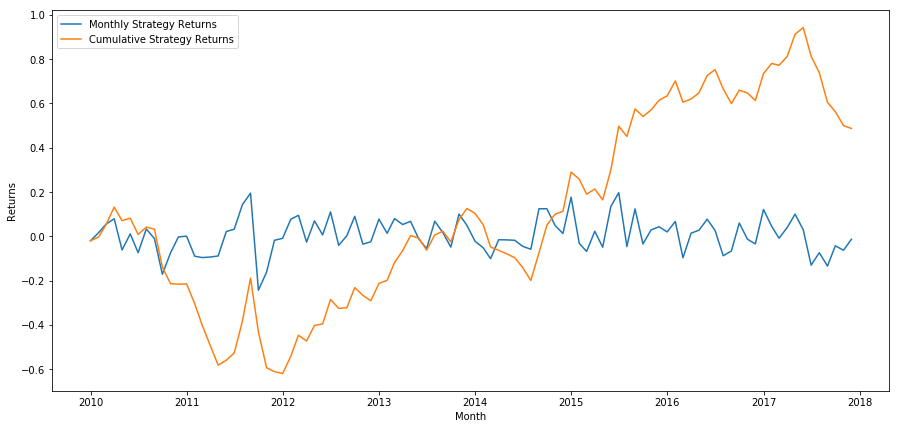
अंत में, यदि हम हर महीने अंतिम टोकरी को लंबा करते हैं और पहली टोकरी को छोटा करते हैं, तो आइए रिटर्न देखें (प्रत्येक प्रतिभूति के लिए समान पूंजी आवंटन मानें) ।

total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

वार्षिक रिटर्न दरेंः 5.03%

हम देख सकते हैं कि हमारे पास एक बहुत ही कमजोर रैंकिंग योजना है, जो उच्च प्रदर्शन वाले शेयरों को निम्न प्रदर्शन वाले शेयरों से केवल बारीकी से अलग कर सकती है। इसके अलावा, यह रैंकिंग योजना सुसंगत नहीं है और हर महीने बहुत भिन्न होती है।

सही रैंकिंग योजना खोजें

लंबी-छोटी संतुलित इक्विटी रणनीति का एहसास करने के लिए, वास्तव में, आपको केवल रैंकिंग योजना निर्धारित करने की आवश्यकता है। उसके बाद सब कुछ यांत्रिक है। एक बार जब आपके पास लंबी-छोटी संतुलित इक्विटी रणनीति हो जाती है, तो आप बहुत अधिक परिवर्तन के बिना विभिन्न रैंकिंग कारकों का आदान-प्रदान कर सकते हैं। यह आपके विचारों को हर बार सभी कोड को समायोजित करने की चिंता किए बिना जल्दी से पुनरावृत्ति करने का एक बहुत ही सुविधाजनक तरीका है।

रैंकिंग योजना लगभग किसी भी मॉडल से भी आ सकती है। यह जरूरी नहीं कि मूल्य-आधारित कारक मॉडल हो। यह एक मशीन लर्निंग तकनीक हो सकती है जो एक महीने पहले रिटर्न की भविष्यवाणी कर सकती है और इस स्तर के अनुसार रैंक कर सकती है।

रैंकिंग योजना का चयन और मूल्यांकन

रैंकिंग योजना दीर्घ-अल्प संतुलित इक्विटी रणनीति का लाभ और सबसे महत्वपूर्ण हिस्सा है। एक अच्छी रैंकिंग योजना चुनना एक व्यवस्थित परियोजना है, और कोई आसान उत्तर नहीं है।

एक अच्छा प्रारंभिक बिंदु मौजूदा ज्ञात प्रौद्योगिकियों का चयन करना है और देखें कि क्या आप उच्च रिटर्न प्राप्त करने के लिए उन्हें थोड़ा संशोधित कर सकते हैं। यहां हम कई प्रारंभिक बिंदुओं पर चर्चा करेंगेः

• क्लोन और समायोजनः एक विषय चुनें जिस पर अक्सर चर्चा की जाती है, और देखें कि क्या आप लाभ प्राप्त करने के लिए इसे थोड़ा संशोधित कर सकते हैं। आम तौर पर, सार्वजनिक रूप से उपलब्ध कारकों के पास अब ट्रेडिंग सिग्नल नहीं होंगे, क्योंकि वे पूरी तरह से बाजार से बाहर हो गए हैं। लेकिन कभी-कभी वे आपको सही दिशा में ले जाएंगे।

• मूल्य निर्धारण मॉडलः भविष्य के रिटर्न की भविष्यवाणी करने वाला कोई भी मॉडल एक ऐसा कारक हो सकता है जिसका उपयोग संभावित रूप से व्यापार वस्तुओं की अपनी टोकरी को रैंक करने के लिए किया जा सकता है। आप किसी भी जटिल मूल्य निर्धारण मॉडल को ले सकते हैं और इसे रैंकिंग योजना में परिवर्तित कर सकते हैं।

• मूल्य-आधारित कारक (तकनीकी संकेतक): मूल्य-आधारित कारक, जैसा कि आज चर्चा की गई है, प्रत्येक इक्विटी के ऐतिहासिक मूल्य के बारे में जानकारी प्राप्त करते हैं और इसका उपयोग कारक मूल्यों को उत्पन्न करने के लिए करते हैं। उदाहरण चलती औसत संकेतक, गति संकेतक या अस्थिरता संकेतक हो सकते हैं।

• प्रतिगमन और गतिः यह ध्यान देने योग्य है कि कुछ कारकों का मानना है कि एक बार कीमतें एक दिशा में चले जाने के बाद, वे ऐसा करना जारी रखेंगे, जबकि कुछ कारक बिल्कुल विपरीत हैं। दोनों अलग-अलग समय क्षितिज और परिसंपत्तियों के लिए प्रभावी मॉडल हैं, और यह अध्ययन करना महत्वपूर्ण है कि क्या मूल व्यवहार गति या प्रतिगमन पर आधारित है।

• मूलभूत कारक (मूल्य आधारित): यह मूलभूत मूल्यों का एक संयोजन है, जैसे कि पीई, लाभांश आदि। मूलभूत मूल्य में कंपनी के वास्तविक दुनिया के तथ्यों से संबंधित जानकारी होती है, इसलिए यह कई पहलुओं में कीमत से अधिक शक्तिशाली हो सकती है।

अंततः, विकास का पूर्वानुमान एक हथियारों की दौड़ है, और आप एक कदम आगे रहने की कोशिश कर रहे हैं। कारक बाजार से मध्यस्थता करेंगे और एक उपयोगी जीवन होगा, इसलिए आपको लगातार यह निर्धारित करने के लिए काम करना चाहिए कि आपके कारकों ने कितने मंदी का अनुभव किया है और क्या नए कारकों का उपयोग उन्हें बदलने के लिए किया जा सकता है।

अन्य विचार

• पुनः संतुलन की आवृत्ति

प्रत्येक रैंकिंग प्रणाली थोड़ा अलग समय सीमा में रिटर्न की भविष्यवाणी करती है। कीमत पर आधारित औसत प्रतिगमन कुछ दिनों में अनुमानित हो सकता है, जबकि मूल्य पर आधारित कारक मॉडल कुछ महीनों में अनुमानित हो सकता है। यह महत्वपूर्ण है कि मॉडल को भविष्यवाणी करने के लिए समय सीमा निर्धारित करें, और रणनीति को निष्पादित करने से पहले सांख्यिकीय सत्यापन करें। बेशक, आप पुनः संतुलन आवृत्ति को अनुकूलित करने की कोशिश करके ओवरफिट नहीं करना चाहते हैं। आप अनिवार्य रूप से एक यादृच्छिक आवृत्ति पाएंगे जो अन्य आवृत्तियों की तुलना में बेहतर है। एक बार जब आप रैंकिंग योजना भविष्यवाणी की समय सीमा निर्धारित कर लेते हैं, तो अपने मॉडल का पूरा उपयोग करने के लिए लगभग इस आवृत्ति पर पुनः संतुलन करने का प्रयास करें।

• पूंजी क्षमता और लेनदेन की लागत

प्रत्येक रणनीति में न्यूनतम और अधिकतम पूंजी मात्रा होती है और न्यूनतम सीमा आमतौर पर लेनदेन लागत से निर्धारित होती है।

बहुत अधिक शेयरों का व्यापार करने से लेनदेन की उच्च लागत होगी। यदि आप 1,000 शेयर खरीदना चाहते हैं, तो प्रत्येक पुनर्वित्त पर हजारों डॉलर खर्च होंगे। आपकी पूंजी का आधार पर्याप्त रूप से उच्च होना चाहिए ताकि लेनदेन की लागत आपकी रणनीति द्वारा उत्पन्न रिटर्न का एक छोटा सा हिस्सा हो सके। उदाहरण के लिए, यदि आपकी पूंजी $100,000 है और आपकी रणनीति प्रति माह 1% ($1,000) कमाती है, तो ये सभी रिटर्न लेनदेन की लागत से खपत हो जाएंगे। आपको 1,000 से अधिक शेयरों को अर्जित करने के लिए लाखों डॉलर की पूंजी के साथ रणनीति चलाने की आवश्यकता है।

सबसे कम परिसंपत्ति सीमा मुख्य रूप से कारोबार किए जाने वाले शेयरों की संख्या पर निर्भर करती है। हालांकि, अधिकतम क्षमता भी बहुत अधिक है। लंबी-लघु संतुलित इक्विटी रणनीति लाभ खोए बिना सैकड़ों मिलियन डॉलर का व्यापार कर सकती है। यह एक तथ्य है, क्योंकि यह रणनीति अपेक्षाकृत कम बार पुनर्व्यवस्थित होती है। प्रत्येक शेयर का डॉलर मूल्य बहुत कम होगा जब कुल परिसंपत्तियों को कारोबार किए गए शेयरों की संख्या से विभाजित किया जाता है। आपको इस बारे में चिंता करने की ज़रूरत नहीं है कि क्या आपकी ट्रेडिंग मात्रा बाजार को प्रभावित करेगी। मान लीजिए कि आप 1,000 शेयरों का व्यापार करते हैं, यानी 100,000,000 डॉलर। यदि आप हर महीने पूरे पोर्टफोलियो को पुनर्व्यवस्थित करते हैं, तो प्रत्येक शेयर केवल 100,000 डॉलर प्रति माह का व्यापार करेगा, जो अधिकांश प्रतिभूतियों के लिए एक महत्वपूर्ण बाजार होने के लिए पर्याप्त नहीं है।

संबंधित

अधिक