Rumus Kelly - alat yang ampuh untuk kontrol posisi

Asumsikan bahwa Anda menang 60% dan kalah 40%; Anda menang 100% dan kalah 100%. Jika Anda menang, Anda akan menang satu dolar per dolar, dan jika Anda kalah, Anda akan kehilangan satu dolar per dolar. Asumsikan bahwa Anda menang tanpa batas waktu, dan setiap taruhan Anda sendiri.

• 1. Untuk taruhan ini, keuntungan yang diharapkan dari setiap taruhan adalah 60% dari jumlah yang dipertaruhkan*1-40%*1 = 20%, ekspektasi keuntungan positif. Artinya, ini adalah kebuntuan yang menguntungkan para hacker, dan memiliki keuntungan yang sangat besar.

Jadi bagaimana kita bisa bertaruh?

Jika kita tidak berpikir secara serius, bayangkan secara kasar, kita akan merasa bahwa karena keuntungan yang saya harapkan dari setiap taruhan adalah 20%, maka untuk mencapai keuntungan maksimum dalam jangka panjang, saya harus berusaha untuk menempatkan sebagian besar modal dalam setiap taruhan.

Tapi jelas setiap permainan judi dimasukkan ke dalam 100% dari modal tidak masuk akal, karena jika salah satu permainan judi kalah, maka semua modal akan hilang, tidak dapat lagi berpartisipasi dalam permainan berikutnya, hanya bisa diam-diam meninggalkan permainan.

Jadi, kesimpulannya adalah bahwa jika ada peluang yang sangat kecil untuk kehilangan semua dana Anda dalam satu kesempatan, maka Anda tidak akan pernah memiliki posisi penuh. Karena dalam jangka panjang, kejadian probabilitas kecil pasti terjadi, dan dalam kehidupan nyata, probabilitas sebenarnya dari kejadian probabilitas kecil jauh lebih besar daripada probabilitas teorinya. Inilah efek ekor lebah dalam ilmu keuangan.

• 2 . Kembali ke titik 1 . Jika setiap kali bertaruh 100% tidak masuk akal, bagaimana dengan 99%? Jika setiap kali bertaruh 99%, tidak hanya menjamin tidak akan pernah bangkrut, tetapi dengan keberuntungan mungkin akan menghasilkan keuntungan besar.

Apakah ini benar-benar terjadi?

Kita tidak perlu menganalisis masalah ini secara teoritis, kita bisa melakukan percobaan. Kita mensimulasikan kebuntuan ini, dan setiap kali bertaruh 99%, kita lihat hasilnya.

Simulasi ini sangat sederhana dan dapat dilakukan dengan Excel. Lihat gambar berikut:

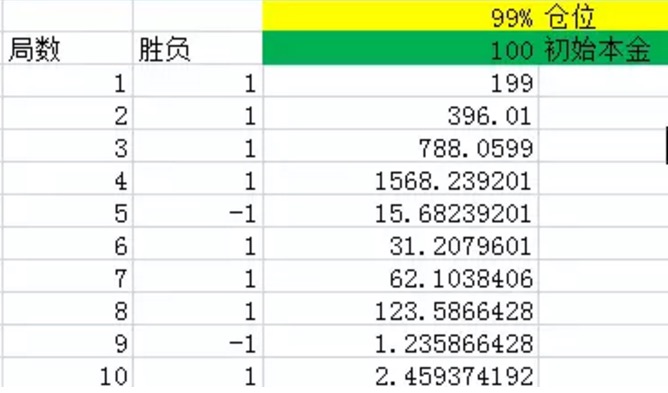Gambar 1

Seperti gambar di atas, kolom pertama menunjukkan jumlah putaran. Kolom kedua adalah kemenangan, Excel akan menghasilkan 1 dengan probabilitas 60%, yaitu probabilitas 60% untuk menghasilkan keuntungan bersih 1,40% untuk menghasilkan -1, yaitu probabilitas 40% untuk menghasilkan keuntungan bersih -1. Kolom ketiga adalah semua dana yang dikumpulkan pada akhir setiap putaran.

Seperti yang dapat dilihat dari gambar, setelah 10 putaran, kemenangan dalam 10 putaran adalah 8, lebih besar dari 60% probabilitas, hanya kalah dua kali. Namun, bahkan dengan demikian, dana terakhir hanya tersisa 2,46 yuan, yang pada dasarnya adalah kerugian.

Dan ketika saya meningkatkan jumlah percobaan menjadi 1000, 2000, 3000, … hasilnya adalah bahwa pada akhirnya, uang yang ada pada tangan saya cenderung menjadi 0.

Karena 99% tidak akan berhasil, mari kita coba dengan beberapa perbandingan lainnya, seperti gambar di bawah ini: Dari gambar ini dapat dilihat bahwa ketika posisi menurun dari 99%, menjadi 90%, 80%, 70%, 60%, hasil dari 10 putaran yang sama sama sekali berbeda. Dari gambar ini dapat dilihat bahwa setelah 10 putaran, dana semakin besar karena posisi semakin kecil.

Jika Anda melihat di sini, Anda akan melihat bahwa masalah ini tidak semudah itu. Bahkan jika Anda menang dalam pertandingan besar seperti itu, Anda tidak akan menang dengan mudah.

Jadi bagaimana cara bertaruh untuk mendapatkan keuntungan maksimal dalam jangka panjang?

Apakah, seperti yang ditunjukkan pada gambar di atas, semakin kecil rasio semakin baik? Tidak, karena jelas tidak ada uang yang bisa dibuat ketika rasio menjadi 0.

Jadi, apa sebenarnya proporsi optimal?

Ini adalah masalah yang harus diselesaikan dengan rumus Kelly yang terkenal!

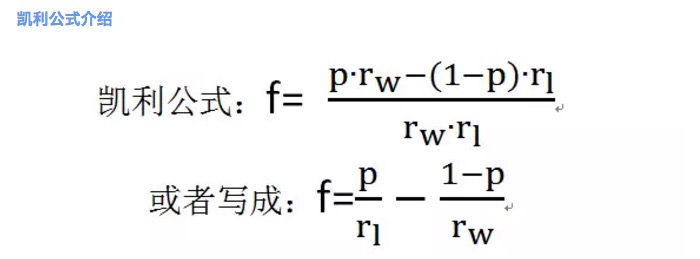Gambar 2

di mana f adalah rasio taruhan yang optimal. P adalah probabilitas kemenangan. Rw adalah tingkat keuntungan bersih saat menang, misalnya rw = 1 dalam permainan 1. Rl adalah tingkat kerugian bersih saat kalah, misalnya rl = 1 dalam permainan 1. Perhatikan bahwa rl > 0

Berdasarkan Rumus Kelly, dapat dihitung bahwa persentase taruhan maksimum dalam Taruhan 1 adalah 20%.

Kita bisa melakukan percobaan untuk lebih memahami kesimpulan ini.

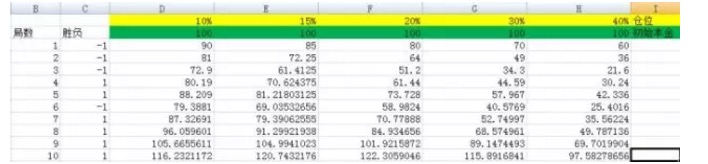Gambar 3

Seperti yang ditunjukkan pada gambar, kita mengatur posisi masing-masing menjadi 10%, 15%, 20%, 30%, 40% . Mereka masing-masing memiliki kolom D, E, F, G, H.

Dan ketika saya mengubahnya menjadi 3000 kali, Dan ketika saya mengubahnya menjadi 5000 kali, saya menemukan bahwa saya tidak dapat melakukan hal itu. Dari sini kita dapat melihat bahwa hasil dari kolom F adalah yang terbesar, dan akar tekanan dibandingkan dengan kolom lainnya bukanlah suatu skala kuantitatif. Sementara itu, persentase posisi kolom F adalah 20%.

Anda melihat kekuatan rumus Kelly. Dalam percobaan di atas, jika Anda tidak beruntung memilih rasio 40%, yaitu kolom H, maka setelah 5.000 putaran, modal Anda berubah dari 100 menjadi 22799985.75, keuntungan yang besar. Namun, dibandingkan dengan hasil rasio 20%, itu sama dengan tidak menghasilkan uang.

Ini adalah kekuatan pengetahuan!

• 3. Memahami Rumus Kelly

Rumus Kelley merupakan sebuah rumus yang sangat kompleks dan membutuhkan pengetahuan matematika yang sangat tinggi. Jadi tidak ada gunanya membahasnya di sini. Di sini saya akan melakukan beberapa eksperimen untuk memperdalam pemahaman subjektif tentang rumus Kelley.

Mari kita lihat sebuah taruhan. taruhan 2: Anda kalah dan menang adalah 50%, misalnya melemparkan koin. Jika Anda menang, Anda akan mendapatkan keuntungan bersih 1, yaitu rw = 1, dan jika Anda kalah, Anda akan mendapatkan kerugian bersih 0,5, yaitu rl = 0,5.

Mudah untuk melihat bahwa keuntungan yang diharapkan dari deadlock 2 adalah 0.25, sebuah deadlock di mana para hacker memiliki keuntungan besar.

Menurut rumus Kelly, kita bisa mendapatkan rasio taruhan terbaik per putaran:

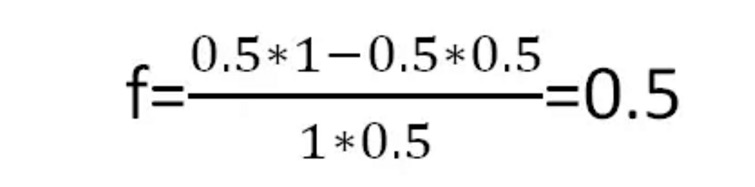Gambar 4

Artinya, setiap kali Anda bertaruh setengah dari uang Anda, Anda akan mendapatkan keuntungan terbesar dalam jangka panjang.

Di bawah ini saya akan memberikan konsep rata-rata tingkat pertumbuhan r berdasarkan percobaan.

Pertama-tama, mari kita lihat dua gambar dari percobaan 2.1:

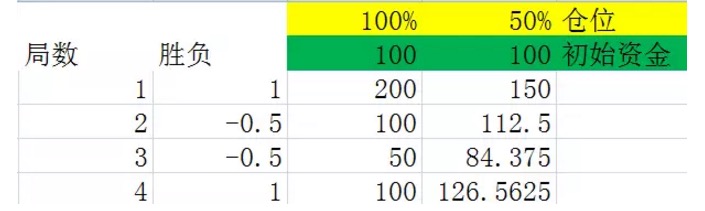Gambar 5

Kedua grafik ini adalah percobaan yang dilakukan untuk mensimulasikan deadlock 2, di kolom kedua menang kolom, percobaan akan menghasilkan 50% probabilitas 1, yang berarti keuntungan 100% ⋅ 50% probabilitas menghasilkan -0.5, yang berarti kerugian 50%. Kolom ketiga dan keempat adalah uang yang dimiliki setelah setiap deadlock dengan posisi 100% dan 50% masing-masing ⋅

Perbandingan yang cermat antara dua gambar dapat menemukan kesimpulan pertama, yaitu setelah melewati jumlah putaran yang sama, hasil akhir hanya berkaitan dengan jumlah putaran yang dimenangkan dan jumlah putaran yang kalah dalam jumlah ini, dan tidak terkait dengan urutan putaran yang dimenangkan dan kalah dalam jumlah ini. Misalnya, dalam dua gambar sebelumnya, 4 putaran juga dilakukan, juga dua putaran yang dimenangkan dan dua putaran yang kalah dalam setiap gambar, tetapi urutan yang kalah dalam gambar pertama adalah menang-kalah-menang, dan urutan yang kalah dalam gambar kedua adalah menang-kalah-menang. Hasil akhirnya sama.

Tentu saja, kesimpulan ini sangat mudah untuk dibuktikan (hukum pertukaran perkalian, anak-anak sekolah dasar bisa melakukannya), namun tidak dibuktikan di sini, dua contoh di atas cukup untuk dipahami oleh semua orang.

Jadi karena hasil akhirnya tidak ada hubungannya dengan urutan kemenangan dan kekalahan, maka kita anggap bahwa impasse 2 akan berjalan seperti percobaan 2.2, lihat gambar berikut:

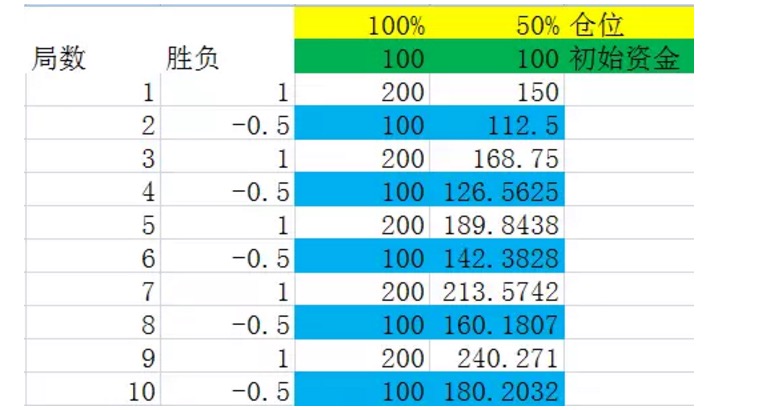Gambar 6

Kami mengasumsikan bahwa kemenangan dan kekalahan dalam undian adalah bergantian, dan karena kesimpulan pertama, dalam jangka panjang, ini tidak berdampak pada hasil.

Sebelum kita melihat gambar sendiri, kita membuat sebuah definisi. Misalkan kita menganggap beberapa pertandingan sebagai satu kesatuan, di mana frekuensi berbagai hasil sama dengan probabilitasnya, dan jumlah pertandingan dari kesatuan ini adalah yang terkecil dari semua kesatuan yang memenuhi persyaratan, maka kita menyebutnya sebagai satu set pertandingan. Misalnya dalam percobaan di atas, satu set pertandingan mewakili dua pertandingan, di mana satu menang dan satu kalah.

Perhatikan dengan seksama angka-angka yang ditandai dengan warna biru di grafik di atas, mereka adalah akhir dari set laga. Anda akan menemukan bahwa angka-angka ini terus tumbuh secara stabil. Ketika posisi adalah 100%, angka yang ditandai dengan warna biru memiliki tingkat pertumbuhan 0%, yaitu tingkat pertumbuhan modal setelah satu set laga.

Ini adalah hukum umum bahwa tingkat pertumbuhan setelah setiap set yang terhenti terkait dengan posisi. Dan semakin besar tingkat pertumbuhan setelah setiap set yang terhenti, semakin besar keuntungan akhir dalam jangka panjang.

Dengan menggunakan tingkat pertumbuhan dari setiap kelompok kebuntuan dapat dihitung rata-rata tingkat pertumbuhan dari setiap kebuntuan g. Dalam gambar di atas, setiap kelompok kebuntuan yang terdiri dari dua kebuntuan, maka rata-rata tingkat pertumbuhan dari setiap kebuntuan

Gambar 7

Dalam jangka panjang, untuk mendapatkan pertumbuhan modal yang maksimal, kita hanya perlu mendapatkan r yang maksimal, yaitu memaksimalkan g. Dan rasio taruhan terbaik f sebenarnya juga diperoleh dengan mencari solusi max ((g)).

• 4. Kesimpulan lain dari Rumus Kelly tentang risiko

Legenda Kelly

Rumus Kelly awalnya dibuat untuk fisikawan AT&T Bell Laboratories John Larry Kelly berdasarkan penelitian rekan-rekannya, Claude Elwood Shannon, tentang perselingkuhan telepon jarak jauh. Kelly memecahkan masalah bagaimana teori informasi Shannon dapat diterapkan pada seorang penjudi yang memiliki informasi inline saat berjudi. Penjudi ingin menentukan jumlah taruhan terbaik, dan informasi inline-nya tidak perlu sempurna (tidak ada perselingkuhan), yang memungkinkan dia memiliki keunggulan yang berguna. Thorpe menggunakan sisa pekerjaannya, melalui perhitungan yang sulit selama beberapa bulan, untuk menulis sebuah makalah matematika berjudul “Menghitung 21 poin untuk memilih strategi bermain poker”. Dia menggunakan pengetahuannya sendiri, dan dalam satu malam dia menyerang semua kasino di kota Reno, Nevada, dan berhasil memenangkan puluhan ribu dolar dari meja taruhan 21 poin. Dia juga adalah nenek moyang dari hedge fund perdagangan kuantitatif di Wall Street, yang menciptakan hedge fund perdagangan kuantitatif pertama di Amerika Serikat pada tahun 1970-an.

Menggunakan Perspektif

Bagaimana Cara Menggunakan Rumus Kelly Untuk Mendapatkan Uang di Dunia Nyata? Dan saya pikir itu adalah untuk menciptakan kebuntuan yang memenuhi persyaratan untuk menggunakan rumus Kelly. Saya baru-baru ini melakukan penelitian tentang sistem perdagangan, apa yang paling penting untuk sistem perdagangan yang baik? Peraturan jual beli dengan ekspektasi keuntungan positif adalah 10% dari pentingnya, dan metode pengendalian dana yang baik adalah 40% dari pentingnya, dan 50% sisanya adalah pengendalian mental orang. Dan rumus Kelly adalah alat yang membantu saya mengendalikan posisi uang saya. Contohnya seperti sistem perdagangan saham yang saya pelajari sebelumnya, sistem ini melakukan perdagangan satu kali seminggu, probabilitas keberhasilan perdagangan setiap minggu adalah 0,8, probabilitas kegagalan adalah 0,2. Ketika berhasil, Anda bisa mendapatkan 3% (dikurangi komisi, pajak cetak), dan setiap kegagalan, Anda akan rugi 5%. Sebelum mengetahui rumus Kelly, saya adalah perdagangan penuh dengan posisi buta, dan tidak tahu posisi saya diatur dengan salah, mental sangat tidak benar. Setelah menggunakan rumus Kelly, posisi terbaik yang dihitung harus 9,33, yaitu jika tingkat bunga pinjaman adalah 0, Anda ingin mendapatkan pertumbuhan modal tercepat, Anda harus menggunakan perdagangan leverage, dengan menghitung rumus mendapatkan r rata-rata pertumbuhan modal per transaksi adalah sekitar 7,44%, sedangkan r rata-rata pertumbuhan modal per transaksi adalah sekitar 1,35 (yaitu, keuntungan yang diharapkan). Tentu saja rumus Kelly tidak bisa semudah itu dalam penerapan praktis, masih banyak kesulitan yang perlu diatasi. Misalnya biaya dana yang dibutuhkan oleh bursa leverage, misalnya bahwa dana tidak dapat dibagi tanpa batas dalam realitas, misalnya bahwa tidak semudah stagnasi sederhana seperti yang disebutkan di atas di pasar keuangan. Tapi bagaimanapun juga, rumus Kelly menunjukkan jalan kita ke depan.