Matematika dan perjudian

• Kita tahu bahwa perjudian adalah permainan probabilitas, dan itu adalah beberapa hasil perjudian yang aneh yang menarik minat matematikawan Pascal dan matematikawan besar Fermat, yang melalui komunikasi surat, mengajukan beberapa prinsip teori probabilitas, sehingga menciptakan teori probabilitas. Hari ini, saya akan memperkenalkan beberapa topik probabilitas dalam perjudian, dan memberi tahu Anda bahwa, untuk bertaruh, Anda harus berpikir dengan cermat.

• 1. Perjudian yang sempurna

Ada pertandingan antara tim NBA, Lakers dan Cowboys, dan kedua tim memiliki penggemar setia, sebut saja mereka orang-orang yang tidak setia dan orang-orang yang tidak setia. Para penggemar tentu saja merasa tim yang mereka dukung lebih mungkin menang, jadi mereka bersedia bertaruh dengan Anda. Misalkan orang-orang yang tidak setia berpikir bahwa kemungkinan Lakers menang adalah p, orang-orang yang tidak setia berpikir bahwa kemungkinan Cowboys menang adalah q, p dan q harus lebih dari 50%.

Metode ini adalah: kita bertaruh pada taruhan yang sama dengan yang dimainkan oleh orang-orang Qin dan orang-orang Qin secara berurutan, jika kita menang, kita akan mendapatkan y, jika kita kalah kita akan kehilangan x, dan jika y > x kita akan menang. Dengan x dan y hanya perlu memenuhi dua persamaan sederhana di bawah ini, harapan keuntungan yang diharapkan dari orang-orang Qin dan orang-orang Qin akan positif, maka kita akan bertaruh dengan kita:

```
p * x - ( 1-p ) * y > 0
q * x - ( 1-q ) * y > 0
```

Ditambah dengan pembatasan y>x, gambar yang digambar adalah area yang dikelilingi oleh tiga garis lurus, dengan nilai koordinat dari titik manapun di dalamnya (x, y) adalah solusi yang menang. Jika p>q, solusinya adalah bagian biru dari gambar berikut:

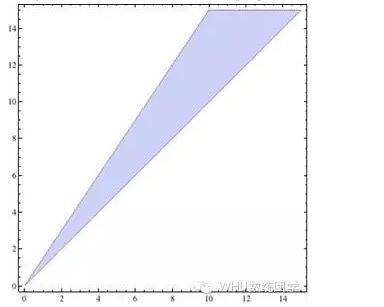
Masalah ini tampaknya telah diselesaikan dengan sempurna, tetapi ada satu keraguan lagi, dan saya yakin pembaca akan segera menemukan absurditasnya: apakah orang-orang Yang atau orang-orang Yang, mereka memiliki ekspektasi pendapatan yang positif, yang berarti bahwa mereka akan menghasilkan uang dalam jangka panjang, sementara kita tidak menghasilkan uang, dari mana semua uang itu datang, dan bagaimana mungkin semua orang menghasilkan uang?

• ### 2, 3 penipuan kartu

Ini adalah teka-teki lain yang cerdik, kita pertama-tama memiliki tiga kartu, kartu nomor 1 berhadapan dengan hitam, kartu nomor 2 berhadapan dengan merah, kartu nomor 3 berhadapan dengan hitam, dan kartu nomor 3 berhadapan dengan merah. Kemudian letakkan kartu-kartu itu ke dalam kotak, goyangkan, dan biarkan lawan menarik satu kartu yang rata di atas meja.

Sebenarnya peluang kita untuk menang bukanlah ¹⁄₂, melainkan ²⁄₃, dan bagian yang paling membingungkan dari teka-teki ini adalah dua sisi kartu. Pemain tidak menarik tiga kartu, melainkan enam kartu: tiga sisi hitam, tiga sisi merah.

Ketika pemain menarik ke sisi hitam, yaitu tiga kemungkinan A, C, D, dan lain-lain, sisi belakangnya adalah D, F, dan A, dengan sisi hitam menyumbang ²⁄₃ dari kemungkinan tersebut.

Pertanyaan ini pertama kali dikemukakan pada tahun 1889 oleh matematikawan Prancis Joseph Louis François Bertrand, dan karena hasilnya yang tidak terduga, ia disebut sebagai paradoks kotak Bertrand. Pada tahun 1950, matematikawan Amerika Warren Weaver memperkenalkan permainan kartu di atas, yang disebut Martin Gardner sebagai penipuan tiga kartu.

• ### 3 Buah Cengkeh A Yang Tak Biasa

Kadang-kadang kita berjudi di awal akan melepaskan air, pertama-tama membiarkan orang lain memenangkan beberapa uang kecil, meletakkan garis panjang untuk menangkap ikan besar, dan akhirnya satu-satunya permainan berakhir. Berikut adalah contoh yang sempurna. Empat orang bermain bridge, saya pertama-tama berkata: mari bermain dadu, saya sekarang memiliki A, Anda menebak apakah saya memiliki lebih banyak A?

Banyak orang pasti berpikir bahwa dua buah jeruk sama sekali tidak berbeda, ditambah satu buah jeruk pun tidak masalah. Namun, perbedaan antara keduanya sangat luar biasa.

  没有A的情形：C（48，13）
  至少有1张A的情形：C（52，13）－C（48，13）
  恰好有1张A的情形：4＊C（48，12）
  至少有2张A的情形：C（52，13）－C（48，13）－4＊C（48，12）
  事件X为至少有两张A，事件Y为至少有一张A，那么条件概率为：

  P（X｜Y）＝P（XY）／P（Y）=(C（52，13）－C（48，13）－4＊C（48，12）)/(C（52，13）－C（48，13）)≈37%

Pada saat ini saya harus bertaruh bahwa saya masih memiliki A, lebih mudah untuk kalah. Tapi setelah saya memasang taruhan pertama, semua orang ingin bertaruh, setelah melihat taruhan kedua, apakah saya akan mengganti pakaian saya, mereka bertaruh lebih banyak, dan kemudian saya tidak memiliki A lagi, di tengah-tengah kita. Di bawah ini kita akan menemukan kemungkinan taruhan kedua yang sangat berbeda:

  有黑桃A的情形：C（51，12）
  没有其它A的情形：C（48，12）
  还有其它A的情形：C（51，12）－C（48，12）
  事件X为还有其它A，事件Y为有黑桃A，条件概率为：

  P（X｜Y）＝P（XY）／P（Y）＝（C（51，12）－C（48，12））／C（51，12）≈56%。

Dikutip dari WHU Aritmatika