Pernyataan hak cipta: Jika Anda ingin mengkompilasi kode artikel ini, silakan sebutkan sumbernya. Jika Anda ingin menggunakan kode untuk tujuan komersial, silakan menulis artikel secara pribadi atau hubungi penulis di [email protected]

1. Pendahuluan

Keuntungan dari transaksi kuantitatif

Perdagangan kuantitatif mengacu pada penilaian subjektif yang dibuat oleh manusia dengan penggantian model matematika canggih, menggunakan teknologi komputer dari data historis yang besar untuk membuat strategi untuk membuat berbagai kemungkinan terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya terjadinya ter          Karena mata uang digital 24*Kontinuitas pasar transaksi 7 jam tanpa henti, dan perdagangan kuantitatif dapat mencapai efek perdagangan frekuensi tinggi, mulai dari pasar mata uang digital jelas merupakan awal yang baik untuk melakukan kuantitas. Saat ini pasar mata uang digital masih belum matang.

Model GQNR

Model ini didasarkan pada model Garch untuk memprediksi volatilitas, menggunakan regresi non-linear untuk memprediksi volatilitas dengan nilai VaR regresi desimal, misalnya GA untuk memprediksi VaR teratas dan VaR terbawah pada siklus berikutnya. Model ini disebut GQNR.

1. Modul Garch

Dalam artikel ini, kami akan membahas lebih lanjut tentang inti dari strategi Garch, sebuah metode yang digunakan di pasar keuangan, dan memiliki efek prediktif pada mata uang digital.

1.1 Definisi Garch

Intinya dari model ARCH adalah menggunakan sekuen kuadrat residu untuk mengadaptasi nilai-nilai fungsi diferensial saat ini dengan perpindahan datar berskala q. Karena model rata-rata bergerak memiliki k-skala intersectionality, model ARCH sebenarnya hanya berlaku untuk fungsi diferensial dengan koefisien korespondensi pendek. Namun dalam prakteknya, beberapa fungsi diferensial dari urutan residu yang bersifat long-term self-relevant, dengan menggunakan ARCH model yang sesuai dengan fungsi diferensial diferensial, akan menghasilkan tingkat rata-rata bergerak yang sangat tinggi, meningkatkan kesulitan estimasi parameter dan akhirnya mempengaruhi akurasi yang sesuai dengan model ARCH.          Untuk memperbaiki masalah ini, sebuah model diferensial kondisional regresif yang luas, yang disingkat sebagai GARCH ((p,q), diusulkan. Model GARCH sebenarnya adalah sebuah model ARCH yang didasari oleh regresi dari fungsi diferensial p yang diperhitungkan, yang dapat secara efektif menyesuaikan fungsi diferensial dengan memori jangka panjang. Model ARCH adalah contoh khusus dari model GARCH, yaitu model GARCH dengan p = 0 (p,q).

1.2 Proses ARCH

Definisi σn adalah estimasi volatilitas aset pada siklus perdagangan n-1 dan mu adalah tingkat pengembalian harian, maka estimasi tanpa bias dapat dibuat berdasarkan tingkat pengembalian pada siklus perdagangan m terakhir: $\( \sigma *n^2= \frac{1}{m-1} \sum\limits*{i=1}^m {( { \mu_{n-i}- \overline{\mu} } ) ^2}, \)\(         melakukan perubahan berikut: 1 mengubah μn-i menjadi persentase yield; 2 mengubah m-1 menjadi m; 3 asumsikan μ = 0, dan perubahan ini tidak terlalu berpengaruh pada hasil, berdasarkan rumus di atas, tingkat fluktuasi dapat disederhanakan menjadi: \)\( \sigma *n^2= \frac{1}{m} \sum\limits*{i=1}^m { \mu_{n-i} ^2}, \)\(         Artinya, setiap siklus rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata-rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata rata \)\( \sigma *n^2= \sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)$         αi adalah koefisien dari kuadrat tingkat pengembalian untuk siklus perdagangan i, mengambil nilai positif dan nilai i yang lebih kecil, semakin besar, jumlah beratnya adalah 1. Lebih lanjut, asumsikan ada sebuah varian jangka panjang VL, dan berat yang sesuai adalah γ, dapat diperoleh berdasarkan persamaan di atas:

\[ \begin{cases}\sigma *n^2= \gamma V*{L}+\sum\limits_{i=1}^m { \alpha_i\mu_{n-i} ^2}\ &\ \gamma+\sum\limits_{i=1}^m{\alpha_i\mu_{n-i}^2}=1 & \end{cases} , \]

        Jadiω=γVL, rumus(15) dapat dituliskan sebagai: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)\( Dari persamaan di atas kita bisa mendapatkan proses ARCH yang umum \)\( \sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2}, \)$

1.3 Proses GARCH

Model GARCH (p,q) adalah kombinasi dari model ARCH (p) dan EWMA (q), yang berarti bahwa volatilitas tidak hanya terkait dengan pendapatan periode sebelumnya (p), tetapi juga terkait dengan periode sebelumnya (q), yang dinyatakan sebagai berikut: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}+\sum\limits_{i=1}^m { \beta_i\sigma_{n-i} ^2}, \)\(         Berdasarkan persamaan di atas kita bisa mendapatkan GARCH yang umum ((1,1)): \)\( \begin{cases}\sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2+\beta\sigma_{n-1}^2}\&\ \qquad\alpha+\beta+\gamma=1 & \end{cases} , \)$

2 Modul QR

Bagian ini akan menjelaskan pengembalian pecahan dasar dan menjelaskan pentingnya pecahan strategis.

Definisi QR

Regresivitas desimal adalah metode pemodelan untuk memperkirakan hubungan linier antara satu set variabel regresi X dan desimal dari variabel Y yang sedang dijelaskan. Model regresi sebelumnya sebenarnya adalah ekspektasi kondisional dari variabel yang diinterpretasikan. Ada juga pertimbangan tentang hubungan antara variabel yang diinterpretasikan dan rata-rata dari distribusi variabel yang diinterpretasikan. Ini pertama kali dikemukakan oleh Koenker dan Bassett pada tahun 1978.

2.2 Dari OLS ke QR

Retorsi umum adalah perkalian dua terkecil, yaitu kuadrat dari pengurangan kesalahan: $\( min \sum{({y_i- \widehat{y}*i })}^2 \)\(         sedangkan tujuan dari pecahan adalah untuk meminimalkan nilai mutlak kesalahan bertimbangan berdasarkan rumus di atas dan: \)\( \mathop{\arg\min*\beta}\ \ \sum{[{\tau(y_i-X_i\beta)^++(1-\tau)(X_i\beta-y_i) ^+ }]} \)$

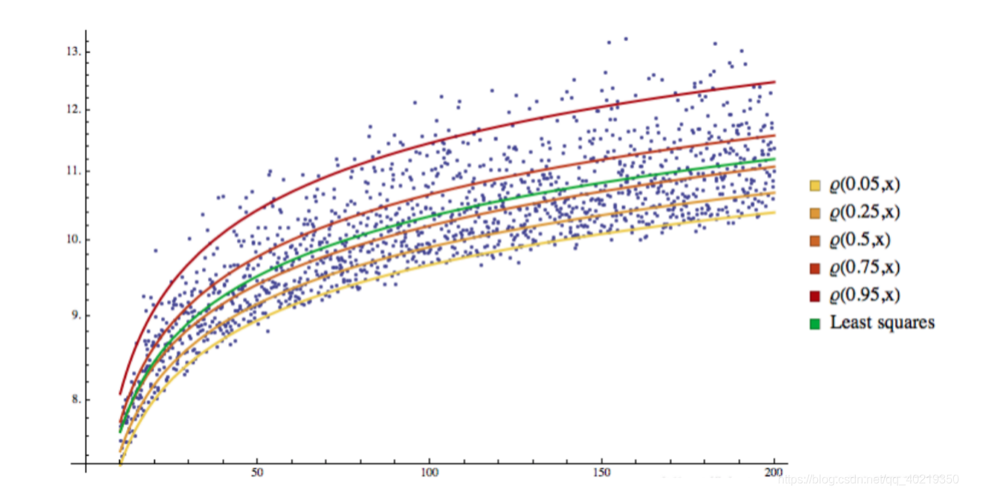
2.2 Visualisasi QR

Anda dapat melihat bahwa semua sampel dibagi menjadi ruang yang berbeda oleh garis regresi, dan garis regresi ini juga menjadi garis pembagian.

3. Kembalikan GARCH-QR

3.1 Mengambil bentuk regresi dari volatilitas dan VaR

        Karena ini adalah inti dari strategi, saya hanya akan memberikan satu bentuk untuk menjelaskan ide tersebut. $\( VaR=\epsilon+W^TE\E=(\zeta,\zeta^2,\zeta^3,\zeta^4)\W=(W_1,W_2,W_3,W_4) \)$

3.2 Menentukan fungsi target

Berdasarkan informasi di atas, kita dapat mengkombinasikan fungsi target yang akan dioptimalkan: $\( \widehat{W}=\mathop{\arg\min_W}\ \ \sum{[{\alpha(VaR_t-W^TE_t)^++(1-\alpha)(W^TE_t-VaR_t) ^+ }]} \)$

3.3 Mengoptimalkan fungsi target menggunakan pembelajaran mesin

Langkah ini lebih bersifat opsional, gradien tradisional menurun, dan algoritma genetik juga tersedia, sehingga pembaca dapat menggunakan kreativitas mereka sendiri untuk bereksperimen.Ada tentang algoritma GA alamat

Ketiga, bagaimana menggunakan GQNR dalam kuantitas

1. Kepastian ide

Inti dari GQNR adalah volatilitas pasar, di setiap titik waktu saat ini, dapat diprediksi oleh GARCH untuk prediksi volatilitas periode berikutnya, di sisi lain, dengan pengembalian desimal dari volatilitas prediksi data masa lalu, dapat memperoleh threshold volatilitas yang tidak akan melampaui batas atas dan bawah dalam kemungkinan besar. Dan kedua batas ini adalah inti dari keseluruhan.

2. Kesulitan penggunaan

• Mengambil bentuk regresi
• Pemilihan algoritma adaptif
• Parameter yang cocok untuk pembelajaran mesin
• Ketidakpastian dan acak pasar

3. Solusi

• Memperpendekatan siklus belajar strategi
• Mengurangi risiko jangka panjang dari sekuritas tunggal
• Meningkatkan verifikasi bersama tren dua rata-rata dan konfirmasi penurunan nilai sekunder