Daun bawang dan spread bid-ask: Studi pendahuluan pada model EKOP

• 1 Pambuka

  Terlalu sibuk akhir-akhir ini, beberapa bulan telah berlalu sejak saya menulis artikel terakhir. Beberapa bulan ini banyak hal yang terjadi, beberapa di antaranya adalah bulan-bulan yang gelap bagi hidup saya sendiri. Namun, pengalaman ini mengajarkan saya bahwa kehidupan, seperti halnya perdagangan, penuh dengan pasang surut dan ketidaktahuan.

  Kita semua tahu bahwa saham yang aktif dalam perdagangan biasanya memiliki spread yang lebih kecil, sedangkan saham yang tidak aktif dalam perdagangan sebaliknya. Mengapa hal ini terjadi? Bisakah kita menggunakan model matematika yang sederhana dan indah untuk menjelaskan perbedaan harga?[1] Pada awalnya, tujuan kami adalah untuk mempelajari apakah perilaku pedagang yang memiliki informasi yang berbeda adalah penyebab perbedaan antara dua jenis harga saham. Dalam artikel ini, saya akan membahas dasar-dasar model ini.

• 2 Asumsi Proses Transaksi

  Ketika kita berbicara tentang model keuangan, yang paling penting adalah memperhatikan asumsi model tersebut. Model keuangan yang baik memiliki asumsi yang tepat: itu tidak akan terlalu kuat sehingga tidak universal; itu tidak akan terlalu lemah sehingga tidak dapat menyimpulkan hasil yang cantik dan ringkas. Asumsi dasar dari model EKOP adalah sebagai berikut:

  Hipotesis 1: Kami membahas perdagangan saham, perdagangan dilakukan pada hari yang terpisah, hipotesis berturut-turut dalam sehari. Artinya, perdagangan pedagang terjadi pada 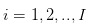hari-hari perdagangan yang terpisah. Dan dalam hari perdagangan, perdagangan terjadi pada 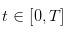waktu berturut-turut seperti itu.

  • Berita buruknya, kami mencatat nilai saham sebagai
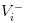
  • Kabar baiknya, kami mencatat nilai saham sebagai
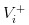
  • Tidak ada berita, kami mencatat nilai saham sebagai

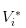
  Jadi jelas, kita memiliki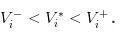

  Hipotesis 2: Pada suatu hari, ada α

  Pada hari-hari di mana suatu peristiwa terjadi, ada probabilitas 1-α untuk kejadian yang tidak mempengaruhi harga saham. Pada hari-hari di mana peristiwa terjadi, ada probabilitasδ untuk kejadian buruk yang akan menurunkan harga saham, dan probabilitas 1-δ untuk kejadian baik yang akan membuat harga saham naik.

  Hipotesis 3: Peserta perdagangan saham terdiri dari pembuat pasar (market maker, disingkat MM), pedagang yang berpengetahuan (informed trader, disingkat IT), dan pedagang yang tidak berpengetahuan (uninformed trader, disingkat UT). Mereka masing-masing mengikuti perilaku perdagangan sebagai berikut:

  MM selalu siap untuk menaikkan satu unit pembelian atau penjualan, memenuhi kewajiban sebagai seorang penjual. MM adalah netral risiko, sehingga harga yang dia tawarkan adalah harga yang menurutnya adil.

  IT hanya berdagang pada hari-hari ketika ada berita, dan mereka berdagang dengan santai. Suatu hari, jika ada berita buruk, ia akan memasang satu tiket penjualan dengan tingkat kedatangan μ; dan pada hari-hari ketika ada berita baik, ia akan memasang satu tiket pembelian dengan tingkat kedatangan μ.

  UT, yaitu orang miskin kita, karena tidak ada berita, mereka melakukan transaksi dengan cara yang tidak terduga, setiap hari, mereka melakukan pembelian dan penjualan dengan harga yang terjangkau.
  Perhatikan bahwa semua proses boson di sini adalah independen satu sama lain. Kita dapat menunjukkan hipotesis 3 dengan sebuah diagram, sebagai berikut:

  

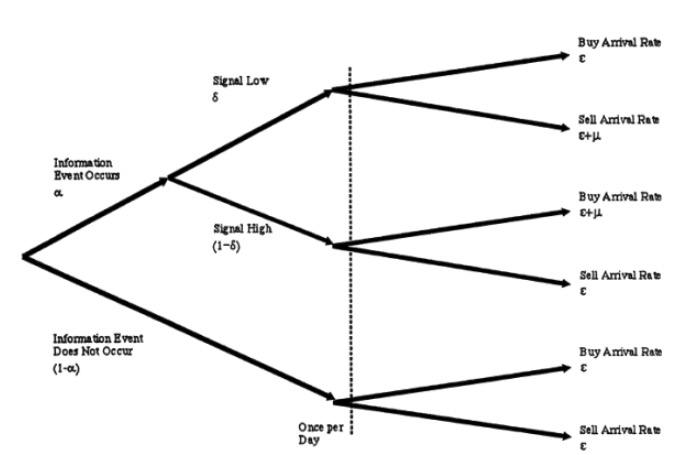
• 3 Pembaruan transaksi dan harga

  Kita tahu bahwa menjadi pedagang pasar biasanya dilakukan oleh perusahaan-perusahaan besar. Mereka sangat cerdas, dalam perjuangan panjang mereka dengan IT dan UT, mereka menyimpulkan semua parameter model dari diagram pohon di atas melalui analisis data historis yang besar. Namun, mereka tidak sepantas pedagang yang berpengetahuan, ketika hari perdagangan akan dimulai, mereka tidak tahu seperti pedagang yang berpengetahuan, apakah ada sesuatu yang penting terjadi di hati mereka hari ini.

  Sekarang, mari kita bereksperimen dengan MM, melawan IT dan UT. Pada titik waktu t, kita mencatat diri kita sendiri sebagai sebuah vektor dari kemungkinan tidak ada, ada hal baik, dan ada hal buruk.

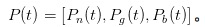  。 Jelas, saya tidak melihat satu pun laporan ketika hari baru saja dimulai, yaitu pada saat /upload/asset/7a5565722b92d2accf331f58923d6bab702659de.png, jadi yang bisa saya katakan adalah bahwa kemungkinan tidak terjadi apa-apa adalah α, kemungkinan terjadi hal baik adalah /upload/asset/c9cf50c6146a25c662c593ed229845822bfac7a5.png, dan kemungkinan terjadi hal buruk adalah /upload/asset/87418f07b12fce65f4c3f70b024e94d2e19f769a.png.

  Bagaimana cara memperbarui probabilitas ini? Nah, kita semua yang melakukan pilihan pasar tahu rumus Bayes. Kita menggunakan hukum Bayes untuk memperbarui perkiraan probabilitas kita sendiri ketika kita melihat ada penjualan.

  

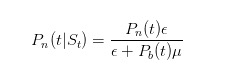
  Rumus ini menyatakan bahwa hanya pedagang yang tidak tahu akan menjual dengan nilai ε ketika tidak ada berita; dan pembagiannya adalah bahwa setiap saat, pedagang yang tidak tahu akan menjual dengan nilai ε, dan pedagang yang tahu hanya akan menjual dengan nilai μ ketika sesuatu yang buruk terjadi. Demikian pula, kita dapat menyimpulkan

  

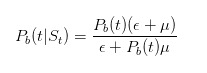
  dan

  

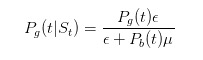
  Sebelum kita lanjutkan dengan deduksi, mari kita lakukan beberapa tes sederhana. Kita mengatakan bahwa jika kita melihat sebuah tiket penjualan, maka kita harus memperbesar perkiraan probabilitas terjadinya sesuatu yang buruk.

  

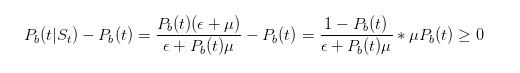
  Dari sini kita bisa melihat bahwa deduksi kita membuktikan intuisi kita.

  Dengan probabilitas yang diperbarui, kita dapat menghitung harga yang adil sebagai harga yang akan kita beli di pasar.

  

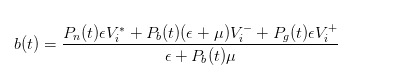
  Dengan deduksi yang sama, kita dapat menemukan bahwa ketika sebuah pesanan datang, harga jual yang kita laporkan sebagai market maker seharusnya

  

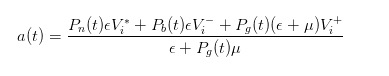
• 4 Ekspresi selisih harga setelah perubahan harga

  Harga beli dan harga jual yang dinyatakan di atas tidak cukup intuitif, kita dapat memasukkan nilai ekspektasi saham pada saat t untuk mempermudah ekspresi.

  

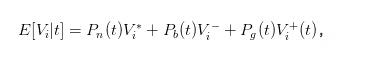
  Jadi kita bisa mengubah bid dan ask menjadi

  

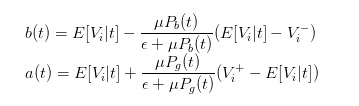
  Jadi, kita bisa jelaskan perbedaan harga sebagai

  

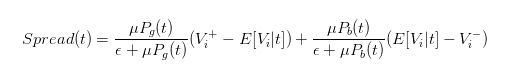
• 5 Pengaruh perilaku pedagang terhadap selisih harga

  Jika kita memiliki ekspresi perbedaan harga, kita dapat menganalisis dampak perbedaan harga dari berbagai pedagang.

  Semakin banyak karet, semakin kecil selisih harga. Perhatikan bahwa ε adalah jumlah penjual yang tidak diketahui (biarlah kita menyebut mereka karet karet), dan jika ε >> μ, kita dapat menemukan, / upload/asset/539e0cfb1aae368277dd0e3840448b6a39abd087.png keduanya akan mendekati 0, yang berarti bahwa spread juga akan mendekati nol.
  Jika kita pergi ke ekstrim lain, asumsikan bahwa tidak ada sawit di pasar, hanya ada sekelompok pedagang yang lebih baik dari sawit, maka kita akan menemukan bahwa harga yang kita pasang adalah 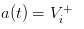dan /upload/asset/1248ca7d3d472490982c9d0aa7b2e04b51269b18.png, sehingga pedagang yang berpengetahuan menemukan diri mereka tidak menguntungkan dalam apa pun yang mereka beli dan jual, pasar pasti akan mati.

  Anda lihat, kita dapat membuat kesimpulan yang menarik dan mendalam berdasarkan beberapa asumsi, menggunakan deduksi matematika yang sangat sederhana, dan mungkin itulah daya tarik besar dari model matematika. Setelah membaca artikel ini, saya juga berharap Anda bisa bersikap baik terhadap ketumbar, karena kita adalah jaminan bahwa pasar dapat melakukan perdagangan yang normal!

[1] Easley, David, et al. "Liquidity, information, and infrequently traded stocks." The Journal of Finance 51.4 (1996): 1405-1436.