Alat yang ampuh untuk Programmatic Trader: Algoritma Pembaruan Inkremental untuk Menghitung Rata-rata dan Variansi
Penulis:FMZ~Lydia, Dibuat: 2023-11-09 15:00:05, Diperbarui: 2024-11-08 09:15:23
Pengantar
Dalam perdagangan terprogram, seringkali perlu untuk menghitung rata-rata dan varians, seperti menghitung rata-rata bergerak dan indikator volatilitas. Ketika kita membutuhkan perhitungan frekuensi tinggi dan jangka panjang, perlu untuk menyimpan data historis untuk waktu yang lama, yang tidak perlu dan memakan sumber daya. Artikel ini memperkenalkan algoritma pembaruan online untuk menghitung rata-rata tertimbang dan varians, yang sangat penting untuk memproses aliran data real-time dan menyesuaikan secara dinamis strategi perdagangan, terutama strategi frekuensi tinggi.
Rata-rata sederhana dan varians
Jika kita menggunakan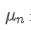 untuk mewakili nilai rata-rata titik data ke-n, dengan asumsi bahwa kita sudah menghitung rata-rata n-1 titik data /upload/asset/28e28ae0beba5e8a810a6.png, sekarang kita menerima titik data baru /upload/asset/28d4723cf4cab1cf78f50.png.
untuk mewakili nilai rata-rata titik data ke-n, dengan asumsi bahwa kita sudah menghitung rata-rata n-1 titik data /upload/asset/28e28ae0beba5e8a810a6.png, sekarang kita menerima titik data baru /upload/asset/28d4723cf4cab1cf78f50.png.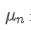 Berikut adalah turunan rinci.
Berikut adalah turunan rinci.
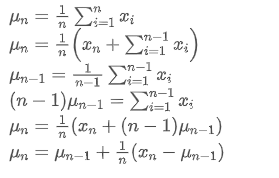
Proses pembaruan varians dapat dipecah menjadi langkah-langkah berikut:
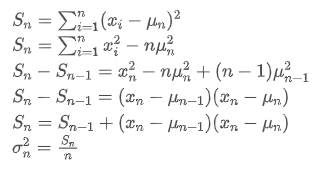
Seperti yang dapat dilihat dari dua rumus di atas, proses ini memungkinkan kita untuk memperbarui rata-rata dan varians baru setelah menerima setiap titik data baru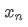 dengan hanya mempertahankan rata-rata dan varians dari data sebelumnya, tanpa menyimpan data historis, membuat perhitungan lebih efisien. Namun, masalahnya adalah bahwa apa yang kita hitung dengan cara ini adalah rata-rata dan varians dari semua sampel, sedangkan dalam strategi yang sebenarnya, kita perlu mempertimbangkan periode tetap tertentu. Mengamati pembaruan rata-rata di atas menunjukkan bahwa jumlah pembaruan rata-rata baru adalah penyimpangan antara data baru dan rata-rata masa lalu dikalikan dengan rasio. Jika rasio ini tetap, itu akan mengarah ke rata-rata tertimbang eksponensial, yang akan kita bahas selanjutnya.
dengan hanya mempertahankan rata-rata dan varians dari data sebelumnya, tanpa menyimpan data historis, membuat perhitungan lebih efisien. Namun, masalahnya adalah bahwa apa yang kita hitung dengan cara ini adalah rata-rata dan varians dari semua sampel, sedangkan dalam strategi yang sebenarnya, kita perlu mempertimbangkan periode tetap tertentu. Mengamati pembaruan rata-rata di atas menunjukkan bahwa jumlah pembaruan rata-rata baru adalah penyimpangan antara data baru dan rata-rata masa lalu dikalikan dengan rasio. Jika rasio ini tetap, itu akan mengarah ke rata-rata tertimbang eksponensial, yang akan kita bahas selanjutnya.
Rata-rata yang ditimbang secara eksponensial
Rata-rata tertimbang eksponensial dapat didefinisikan dengan hubungan rekursif berikut:
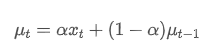
Di antaranya,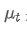 adalah rata-rata tertimbang eksponensial pada titik waktu t,
adalah rata-rata tertimbang eksponensial pada titik waktu t,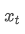 adalah nilai yang diamati pada titik waktu t, α adalah faktor berat, dan
adalah nilai yang diamati pada titik waktu t, α adalah faktor berat, dan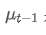 adalah rata-rata tertimbang eksponensial dari titik waktu sebelumnya.
adalah rata-rata tertimbang eksponensial dari titik waktu sebelumnya.
Variansi yang diberi bobot eksponensial
Mengenai varians, kita perlu menghitung rata-rata tertimbang eksponensial dari penyimpangan kuadrat pada setiap titik waktu.
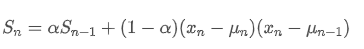
Di antaranya,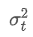 adalah varian tertimbang eksponensial pada titik waktu t, dan
adalah varian tertimbang eksponensial pada titik waktu t, dan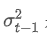 adalah varians tertimbang eksponensial dari titik waktu sebelumnya.
adalah varians tertimbang eksponensial dari titik waktu sebelumnya.
Perhatikan rata-rata dan varians yang diberi bobot eksponensial, pembaruan inkrementalnya intuitif, mempertahankan sebagian dari nilai masa lalu dan menambahkan perubahan baru.https://fanf2.user.srcf.net/hermes/doc/antiforgery/stats.pdf
SMA dan EMA
SMA (juga dikenal sebagai rata-rata aritmatika) dan EMA adalah dua ukuran statistik umum, masing-masing dengan karakteristik dan penggunaan yang berbeda. Yang pertama memberikan bobot yang sama untuk setiap pengamatan, mencerminkan posisi pusat dari set data. Yang terakhir adalah metode perhitungan rekursif yang memberikan bobot yang lebih tinggi untuk pengamatan yang lebih baru.
- Distribusi berat: SMA memberikan bobot yang sama untuk setiap titik data, sementara EMA memberikan bobot yang lebih tinggi untuk titik data yang paling baru.
- Sensitivitas terhadap informasi baru: SMA tidak cukup sensitif terhadap data yang baru ditambahkan, karena melibatkan perhitungan ulang semua titik data.
- Kompleksitas komputasi: Perhitungan SMA relatif sederhana, tetapi karena jumlah titik data meningkat, maka biaya komputasi juga meningkat. Perhitungan EMA lebih kompleks, tetapi karena sifat rekursifnya, dapat menangani aliran data berkelanjutan lebih efisien.
Metode Konversi Perkiraan Antara EMA dan SMA
Meskipun SMA dan EMA berbeda secara konseptual, kita dapat membuat EMA mendekati SMA yang berisi jumlah pengamatan tertentu dengan memilih nilai α yang sesuai.
SMA adalah rata-rata aritmatika dari semua harga dalam jendela waktu tertentu. Untuk jendela waktu N, centroid SMA (yaitu posisi di mana jumlah rata-rata terletak) dapat dianggap sebagai:
pusat SMA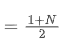
EMA adalah jenis rata-rata tertimbang di mana titik data terbaru memiliki bobot yang lebih besar.
pusat EMA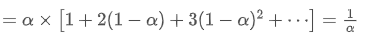
Ketika kita mengasumsikan bahwa SMA dan EMA memiliki centroid yang sama, kita bisa mendapatkan:
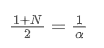
Untuk memecahkan persamaan ini, kita bisa mendapatkan hubungan antara α dan N.
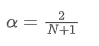
Ini berarti bahwa untuk SMA yang diberikan dari N hari, nilai α yang sesuai dapat digunakan untuk menghitung
Konversi EMA dengan Frekuensi Pembaruan yang Berbeda
Misalkan kita memiliki EMA yang diperbarui setiap detik, dengan faktor bobot /upload/asset/28da19ef219cae323a32f.png. Ini berarti bahwa setiap detik, titik data baru akan ditambahkan ke EMA dengan bobot /upload/asset/28da19ef219cae323a32f.png, sementara pengaruh titik data lama akan dikalikan dengan /upload/asset/28cfb008ac438a12e1127.png.
Jika kita mengubah frekuensi pembaruan, seperti pembaruan sekali setiap f detik, kita ingin menemukan faktor bobot baru /upload/asset/28d2d28762e349a03c531.png, sehingga dampak keseluruhan titik data dalam f detik adalah sama dengan saat diperbarui setiap detik.
Dalam waktu f detik, jika tidak ada pembaruan yang dilakukan, dampak dari titik data lama akan terus menurun f kali, setiap kali dikalikan dengan /upload/asset/28e50eb9c37d5626d6691.png. Oleh karena itu, total faktor peluruhan setelah f detik adalah /upload/asset/28e296f97d8c8344a2ee6.png.
Untuk membuat EMA diperbarui setiap f detik memiliki efek peluruhan yang sama dengan EMA diperbarui setiap detik dalam satu periode pembaruan, kita menetapkan total faktor peluruhan setelah f detik sama dengan faktor peluruhan dalam satu periode pembaruan:
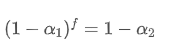
Menyelesaikan persamaan ini, kita mendapatkan faktor berat baru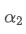
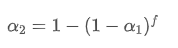
Rumus ini memberikan nilai perkiraan dari faktor bobot baru /upload/asset/28d2d28762e349a03c531.png, yang mempertahankan efek smoothing EMA tidak berubah ketika frekuensi pembaruan berubah.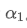 dengan nilai 0,001 dan memperbarui setiap 10 detik, jika diubah menjadi pembaruan setiap detik, nilai setara
dengan nilai 0,001 dan memperbarui setiap 10 detik, jika diubah menjadi pembaruan setiap detik, nilai setara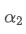 akan sekitar 0,01.
akan sekitar 0,01.
Implementasi Kode Python
class ExponentialWeightedStats:
def __init__(self, alpha):
self.alpha = alpha
self.mu = 0
self.S = 0
self.initialized = False
def update(self, x):
if not self.initialized:
self.mu = x
self.S = 0
self.initialized = True
else:
temp = x - self.mu
new_mu = self.mu + self.alpha * temp
self.S = self.alpha * self.S + (1 - self.alpha) * temp * (x - self.mu)
self.mu = new_mu
@property
def mean(self):
return self.mu
@property
def variance(self):
return self.S
# Usage example
alpha = 0.05 # Weight factor
stats = ExponentialWeightedStats(alpha)
data_stream = [] # Data stream
for data_point in data_stream:
stats.update(data_point)
Ringkasan
Dalam perdagangan terprogram frekuensi tinggi, pemrosesan cepat data real-time sangat penting. Untuk meningkatkan efisiensi komputasi dan mengurangi konsumsi sumber daya, artikel ini memperkenalkan algoritma pembaruan online untuk terus menghitung rata-rata tertimbang dan varians aliran data. Pembaruan inkremental real-time juga dapat digunakan untuk berbagai perhitungan data statistik dan indikator, seperti korelasi antara dua harga aset, penyesuaian linier, dll, dengan potensi besar. Pembaruan inkremental memperlakukan data sebagai sistem sinyal, yang merupakan evolusi dalam pemikiran dibandingkan dengan perhitungan periode tetap.
- Keuntungan Menggunakan API FMZ untuk Manajemen Kontrol Kelompok yang Efisien dalam Perdagangan Kuantitatif
- Kinerja harga setelah mata uang terdaftar pada kontrak abadi
- Menggunakan API ekstensi FMZ untuk mencapai keuntungan dalam manajemen kontrol kelompok yang efisien dalam transaksi kuantitatif
- Performa harga setelah kontrak permanen mata uang
- Hubungan Antara Naik Dan Turunnya Mata Uang Dan Bitcoin
- Hubungan antara penurunan mata uang dan Bitcoin
- Pembahasan singkat tentang keseimbangan buku pesanan di Bursa Terpusat
- Mengukur Risiko dan Pengembalian - Pendahuluan Teori Markowitz
- Percakapan tentang neraca buku pesanan di bursa terpusat
- Mengukur risiko dan imbalan Teori Fumakowitz
- Alat pedagang terprogram: algoritma pembaruan inkremental untuk menghitung rata-rata dan selisih
- Konstruksi dan penerapan kebisingan pasar
- Peningkatan dan Transformasi Faktor PSY
- Analisis Strategi Perdagangan Frekuensi Tinggi - Penny Jump
- Ide Perdagangan Alternatif - Strategi Perdagangan Area K-line
- Konstruksi dan penerapan kebisingan pasar
- Faktor peningkatan dan transformasi PSY
- Analisis strategi perdagangan frekuensi tinggi - Penny Jump
- Cara Mengukur Risiko Posisi - Pendahuluan Metode VaR
- Ide perdagangan alternatif - Strategi perdagangan area K-line