Mengukur Risiko dan Pengembalian - Pendahuluan Teori Markowitz

Minggu lalu, ketika memperkenalkanCara Mengukur Risiko Posisi - Pendahuluan Metode VaRDalam artikel ini, disebutkan bahwa risiko portofolio tidak sama dengan risiko aset individu dan terkait dengan korelasi harga mereka. Mengambil dua aset sebagai contoh, jika korelasi positif mereka sangat kuat, yang berarti mereka naik dan turun bersama, maka investasi diversifikasi tidak akan mengurangi risiko. Jika ada korelasi negatif yang kuat, investasi diversifikasi dapat mengurangi risiko secara signifikan. Pertanyaan alami kemudian muncul: bagaimana kita memaksimalkan pengembalian pada tingkat risiko tertentu ketika berinvestasi dalam portofolio? Ini membawa kita ke Teori Markowitz, yang akan kita perkenalkan hari ini.

Teori portofolio modern (MPT), yang diusulkan oleh Harry Markowitz pada tahun 1952, adalah kerangka kerja matematika untuk pemilihan portofolio. Ini bertujuan untuk memaksimalkan pengembalian yang diharapkan dengan memilih kombinasi aset risiko yang berbeda sambil mengendalikan risiko.

Konsep Kunci Teori Markowitz

1. Tingkat Pengembalian yang Diharapkan: Ini adalah pengembalian yang diharapkan oleh investor untuk menerima dari kepemilikan aset atau portofolio investasi, biasanya diprediksi berdasarkan data pengembalian sejarah.

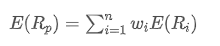
Di mana,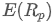adalah pengembalian yang diharapkan dari portofolio,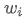adalah bobot aset ke-i dalam portofolio,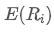adalah pengembalian yang diharapkan dari aset ke-i.

2. Risiko (volatilitas atau standar deviasi): Digunakan untuk mengukur ketidakpastian laba investasi atau volatilitas investasi.

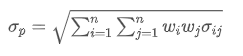
Di mana,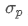mewakili total risiko portofolio,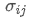adalah kovariansi aset i dan aset j, yang mengukur hubungan perubahan harga antara kedua aset ini.

3. Kovariansi: Mengukur hubungan antara perubahan harga dua aset.

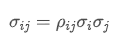
Di mana,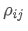adalah koefisien korelasi aset i dan aset j,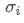dan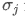adalah masing-masing standar deviasi aset i dan aset j.

4. Perbatasan yang Efisien: Dalam sistem koordinat risiko-pengembalian, batas efisien adalah serangkaian portofolio investasi yang dapat memberikan pengembalian maksimum yang diharapkan pada tingkat risiko tertentu.

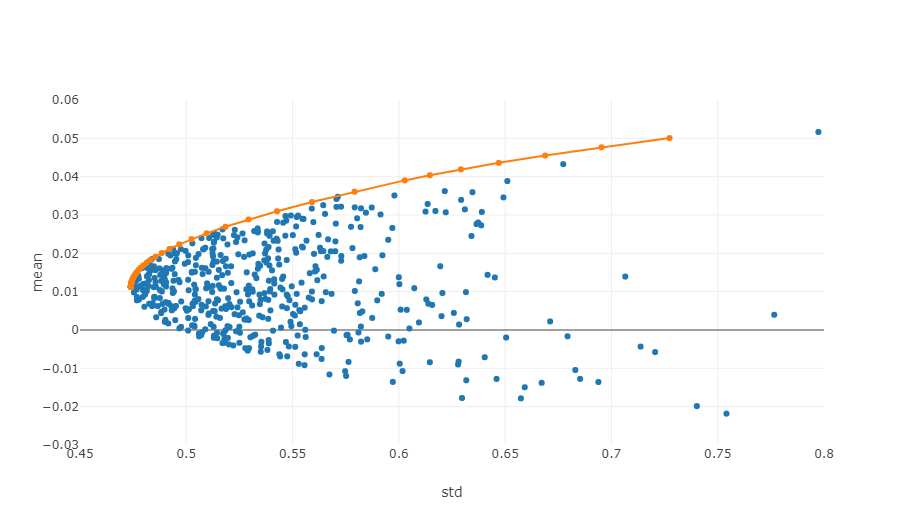
Diagram di atas adalah ilustrasi batas yang efisien, di mana setiap titik mewakili portofolio investasi yang berbeda. sumbu x menunjukkan volatilitas, yang sama dengan tingkat risiko, sementara sumbu y menunjukkan tingkat pengembalian. Jelas, fokus kami terletak di tepi atas grafik karena mencapai pengembalian tertinggi pada tingkat risiko yang setara.

Dalam perdagangan kuantitatif dan manajemen portofolio, penerapan prinsip-prinsip ini membutuhkan analisis statistik data historis dan menggunakan model matematika untuk memperkirakan pengembalian yang diharapkan, standar deviasi dan kovariansi untuk berbagai aset. Kemudian teknik optimasi digunakan untuk menemukan alokasi berat aset terbaik. Proses ini sering melibatkan operasi matematika yang kompleks dan pemrosesan komputer yang luas - inilah sebabnya analisis kuantitatif telah menjadi sangat penting dalam keuangan modern. Selanjutnya, kita akan menggambarkan cara mengoptimalkan dengan contoh Python tertentu.

Contoh Kode Python untuk Menemukan Kombinasi Optimal Menggunakan Metode Simulasi

Perhitungan portofolio optimal Markowitz adalah proses multi-langkah, yang melibatkan beberapa langkah kunci, seperti persiapan data, simulasi portofolio, dan perhitungan indikator.https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. Mendapatkan data pasar:

Melaluiget_dataIni adalah data yang diperlukan untuk menghitung pengembalian dan risiko, yang digunakan untuk membangun portofolio investasi dan menghitung rasio Sharpe.

2. Menghitung Tingkat Pengembalian dan Risiko:

Peraturancalculate_returns_riskFungsi ini digunakan untuk menghitung pengembalian tahunan dan risiko tahunan (deviasi standar) untuk setiap mata uang digital.

3. Hitung Portofolio Optimal Markowitz:

Peraturancalculate_optimal_portfolioFungsi ini digunakan untuk mensimulasikan beberapa portofolio investasi. Dalam setiap simulasi, bobot aset dihasilkan secara acak dan kemudian pengembalian yang diharapkan dan risiko portofolio dihitung berdasarkan bobot ini. Dengan secara acak menghasilkan kombinasi dengan bobot yang berbeda, dimungkinkan untuk mengeksplorasi beberapa portofolio investasi potensial untuk menemukan yang optimal.

Tujuan dari seluruh proses adalah untuk menemukan portofolio investasi yang menghasilkan pengembalian yang diharapkan terbaik pada tingkat risiko tertentu. Dengan mensimulasikan beberapa kombinasi yang mungkin, investor dapat lebih memahami kinerja konfigurasi yang berbeda dan memilih kombinasi yang paling sesuai dengan tujuan investasi dan toleransi risiko mereka.

import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# Obtain market data
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# Calculate Markowitz Optimal Portfolio
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # Convert weights to a list

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# Output results
print("Optimal combination:")
for i in range(len(symbols)):
    print(f"{symbols[i]} Weight: {optimal_weights[i]:.4f}")

print(f"Expected return rate: {optimal_return:.4f}")
print(f"Expected risk (standard deviation): {optimal_risk:.4f}")
print(f"Sharpe ratio: {optimal_return / optimal_risk:.4f}")

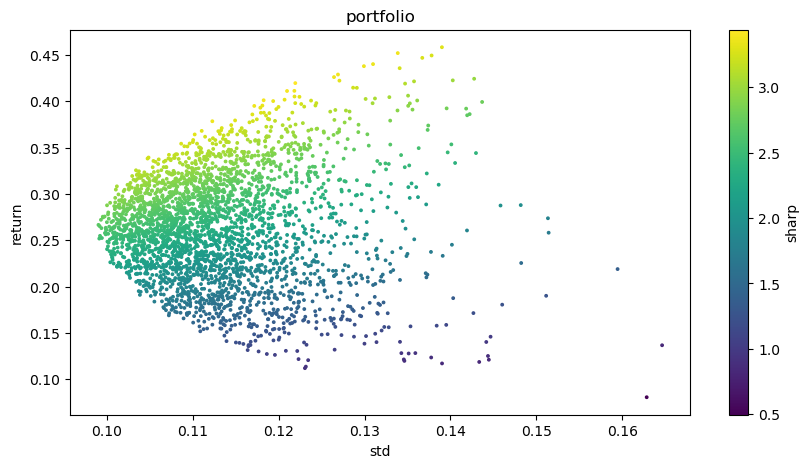
# Visualized investment portfolio
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

Hasil output akhir: Kombinasi yang optimal: Berat BTCUSDT: 0,0721 Berat ETHUSDT: 0.2704 Berat BNBUSDT: 0,3646 Berat LINKUSDT: 0,1892 Berat BCHUSDT: 0,0829 Berat LTCUSDT: 0,0209 Tingkat pengembalian yang diharapkan: 0,4195 Risiko yang diharapkan (deviasi standar): 0,1219 Rasio Sharpe: 3.4403