Statistik Bayesian merupakan disiplin ilmu matematika yang kuat dengan aplikasi luas di banyak bidang, termasuk keuangan, penelitian medis, dan teknologi informasi. Hal ini memungkinkan kita untuk menggabungkan keyakinan sebelumnya dengan bukti untuk sampai pada keyakinan posterior baru, yang memungkinkan kita untuk membuat keputusan yang lebih tepat.

Dalam artikel ini, kami akan memperkenalkan secara singkat beberapa matematikawan utama yang mendirikan bidang ini.

Sebelum Bayes Untuk lebih memahami statistik Bayesian, kita perlu kembali ke abad ke-18 dan merujuk pada matematikawan De Moivre dan makalahnya “Prinsip Peluang”[1]。

Dalam risalahnya, De Moivre membahas banyak masalah pada masanya yang terkait dengan probabilitas dan perjudian. Seperti yang mungkin Anda ketahui, solusinya terhadap salah satu masalah ini mengarah pada asal mula distribusi normal, tetapi itu cerita lain.

Dalam makalahnya ada pertanyaan sederhana:

“Peluang untuk mendapatkan tiga sisi kepala ketika melempar koin yang adil tiga kali berturut-turut.”

Ketika membaca masalah yang dijelaskan dalam “Prinsip Peluang,” Anda mungkin memerhatikan bahwa sebagian besarnya dimulai dengan sebuah hipotesis yang menjadi dasar penghitungan probabilitas suatu kejadian. Misalnya, pada soal di atas, diasumsikan bahwa koinnya adil, jadi peluang muncul sisi kepala dalam lemparan adalah 0,5.

Hal ini diungkapkan dalam istilah matematika saat ini sebagai:

𝑃(𝑋|𝜃)

Tapi bagaimana jika kita tidak tahu apakah koin itu asli? Jika kita tidak tahu𝜃Kain wol?

Thomas Bayes dan Richard Price

Hampir lima puluh tahun kemudian, pada tahun 1763, sebuah makalah berjudul “An Essay on the Principle of Chance”[2] Diterbitkan dalam Philosophical Transactions of the Royal Society of London.

Pada beberapa halaman pertama dokumen tersebut, terdapat teks yang ditulis oleh matematikawan Richard Price, yang merangkum isi makalah yang ditulis oleh temannya Thomas Bayes beberapa tahun sebelum kematiannya. Dalam pendahuluannya, Price menjelaskan pentingnya beberapa penemuan yang dilakukan oleh Thomas Bayes yang tidak tercakup dalam Prinsip Peluang De Moivre.

Sebenarnya, dia mengacu pada suatu masalah spesifik:

“Jika diketahui banyaknya kejadian dan kegagalan suatu peristiwa yang tidak diketahui, carilah peluang kejadian tersebut berada di antara dua tingkat probabilitas yang telah disebutkan.”

Dengan kata lain, setelah mengamati suatu peristiwa, kita menemukan parameter yang tidak diketahuiθBerapa probabilitas antara dua derajat probabilitas? Ini sebetulnya salah satu masalah pertama dalam sejarah yang berkaitan dengan inferensi statistik, dan memunculkan nama probabilitas terbalik. Secara matematika:

𝑃( 𝜃 | 𝑋）

Ini tentu saja apa yang sekarang kita sebut sebagai distribusi posterior teorema Bayes.

Penyebab yang tidak disebabkan

Kenali kedua pendeta tua ini.Thomas BayesDanRichard Harga, apa yang memotivasi penelitian ini sebenarnya sangat menarik. Namun untuk melakukan ini, kita perlu mengesampingkan sejenak beberapa pengetahuan tentang statistika.

Kita berada di abad ke-18, dan probabilitas menjadi bidang yang semakin diminati para matematikawan. Matematikawan seperti De Moivre atau Bernoulli telah menunjukkan bahwa beberapa peristiwa terjadi dengan tingkat keacakan tertentu tetapi masih diatur oleh aturan-aturan tetap. Misalnya, jika Anda melempar dadu berkali-kali, satu dari enam kali lemparannya akan menghasilkan angka enam. Seolah-olah ada aturan tersembunyi yang menentukan nasib peluang.

Sekarang, bayangkanlah Anda adalah seorang matematikawan dan penganut agama yang taat yang hidup di masa ini. Anda mungkin tertarik untuk mengetahui bagaimana aturan tersembunyi ini berhubungan dengan Tuhan.

Ini memang pertanyaan yang ditanyakan oleh Bayes dan Price sendiri. Solusi yang mereka harapkan untuk menyelesaikan masalah ini dapat diterapkan secara langsung untuk membuktikan bahwa “dunia harus merupakan hasil dari kebijaksanaan dan kecerdasan; dengan demikian memberikan bukti keberadaan Tuhan sebagai penyebab akhir”[2] - Artinya, tidak ada sebab dan akibat.

Laplace

Anehnya, sekitar dua tahun kemudian, pada tahun 1774, tampaknya tanpa membaca makalah Thomas Bayes, matematikawan Perancis Laplace menulis sebuah makalah berjudul “On the Causes of Events through the Probabilities of Events”.[3], yang merupakan makalah tentang masalah probabilitas terbalik. Di halaman pertama Anda dapat membaca

Prinsip utamanya adalah:

“Jika suatu kejadian dapat disebabkan oleh n penyebab yang berbeda, maka peluang penyebab-penyebab tersebut untuk suatu kejadian tertentu adalah dalam rasio yang sama dengan peluang kejadian tersebut jika penyebabnya diketahui, dan peluang adanya masing-masing penyebab tersebut adalah sama.” terhadap probabilitas kejadian yang diberikan penyebabnya. Probabilitas penyebabnya, dibagi dengan jumlah probabilitas kejadian yang diberikan masing-masing penyebab tersebut.”

Inilah yang kita kenal sekarang sebagai teorema Bayes:

​

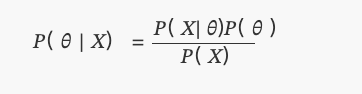
di dalamP(θ)terdistribusi secara merata.

Percobaan Koin

Kami akan membawa statistik Bayesian ke masa kini dengan menggunakan Python dan pustaka PyMC dan melakukan eksperimen sederhana.

Misalkan seorang teman memberi Anda sebuah koin dan bertanya apakah menurut Anda koin itu adil. Karena dia sedang terburu-buru, dia meminta Anda melempar koin hanya 10 kali. Seperti yang Anda lihat, ada parameter yang tidak diketahui dalam masalah inip, peluang munculnya gambar kepala dalam lemparan koin, dan kita ingin memperkirakan hal inipNilai yang paling mungkin dari .

(Catatan: Kami tidak berbicara tentang parameterpadalah variabel acak, tetapi parameternya tetap dan kita ingin mengetahui di antara nilai mana parameter tersebut paling mungkin muncul. )

Untuk mendapatkan perspektif yang berbeda mengenai masalah ini, kami akan membahasnya berdasarkan dua keyakinan awal yang berbeda:

• 1. Anda tidak memiliki informasi sebelumnya tentang kewajaran koin dan menetapkan probabilitas yang sama untukp. Dalam kasus ini, kita akan menggunakan apa yang disebut prior tidak informatif, karena Anda tidak menambahkan informasi apa pun ke keyakinan Anda.
• 1. Anda tahu dari pengalaman bahwa meskipun sebuah koin mungkin tidak adil, sulit untuk membuatnya sangat tidak adil, jadi Anda berpikir parameternyapKemungkinan besar tidak akan turun di bawah 0,3 atau di atas 0,7. Dalam kasus ini, kita akan menggunakan prior informatif.

Untuk kedua kasus tersebut, keyakinan awal kami adalah sebagai berikut:

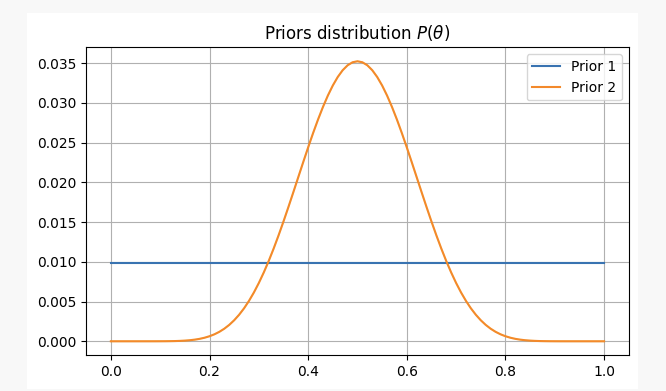
Setelah melempar koin 10 kali, Anda mendapat 2 sisi kepala. Dengan bukti ini, kita mungkin dapat mengetahui di mana menemukan parameter kitap？

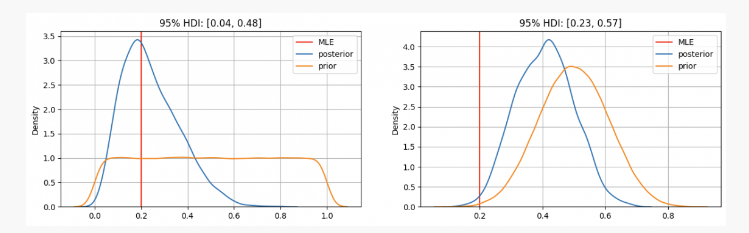
Seperti yang Anda lihat, pada kasus pertama kita memilikipDistribusi sebelumnya berpusat pada estimasi kemungkinan maksimum (MLE)p=0.2, yang merupakan pendekatan serupa menggunakan metode frekuentis. Parameter yang sebenarnya tidak diketahui akan berada dalam interval kredibel 95% antara 0,04 dan 0,48.

Di sisi lain, ketika ada keyakinan tinggi bahwa parameterp Padahal seharusnya berada di antara 0,3 dan 0,7, kita dapat melihat bahwa distribusi posterior berada di sekitar 0,4, yang jauh lebih tinggi daripada nilai yang diberikan oleh MLE kita. Dalam kasus ini, parameter tak diketahui yang sebenarnya akan berada dalam interval kredibel 95% antara 0,23 dan 0,57.

Jadi pada kasus pertama, Anda akan memberi tahu teman Anda bahwa Anda yakin koin itu tidak adil. Namun dalam kasus lain, Anda akan mengatakan kepadanya bahwa Anda tidak yakin apakah koin itu adil.

Seperti yang Anda lihat, bahkan dengan bukti yang sama (2 kepala dari 10 lemparan), hasilnya bisa berbeda karena keyakinan sebelumnya yang berbeda. Inilah kekuatan statistika Bayesian, yang mirip dengan metode ilmiah, memungkinkan kita memperbarui keyakinan kita dengan menggabungkan keyakinan sebelumnya dengan pengamatan dan bukti baru.

END

Dalam artikel hari ini, kita melihat asal usul statistik Bayesian dan kontributor utamanya. Sejak itu, ada banyak kontributor penting lainnya di bidang statistik ini (Jeffreys, Cox, Shannon, dll.), yang direproduksi dari quantdare.com.