Pemodelan dan Analisis Volatilitas Bitcoin Berdasarkan Model ARMA-EGARCH

Baru-baru ini, saya telah melakukan beberapa analisis tentang volatilitas Bitcoin, yang berupa kata-kata dan spontan. Jadi saya hanya berbagi beberapa pemahaman dan kode saya sebagai berikut. Kemampuan saya terbatas, dan kode tidak sangat sempurna. Jika ada kesalahan, tolong tunjukkan dan perbaiki secara langsung.

1. Deskripsi singkat dari seri waktu keuangan

Deret waktu keuangan adalah seperangkat model deret Proses Stochastic berdasarkan variabel yang diamati dalam dimensi waktu. Variabel biasanya adalah tingkat pengembalian aset. Karena tingkat pengembalian independen dari skala investasi dan memiliki sifat statistik, lebih berharga untuk menganalisis peluang investasi aset keuangan yang mendasari.

Di sini, dengan berani diasumsikan bahwa tingkat pengembalian Bitcoin sesuai dengan karakteristik tingkat pengembalian aset keuangan umum, yaitu, ini adalah seri yang lemah halus, yang dapat ditunjukkan dengan pengujian konsistensi beberapa sampel.

1-1. Persiapan, perpustakaan impor, fungsi encapsulate

Konfigurasi lingkungan penelitian telah selesai. Perpustakaan yang diperlukan untuk perhitungan berikutnya diimpor ke sini. Karena ditulis secara intermiten, mungkin berlebihan. Silakan bersihkan sendiri.

Dalam [1]:

'''
start: 2020-02-01 00:00:00
end: 2020-03-01 00:00:00
period: 1h
exchanges: [{"eid":"Huobi","currency":"BTC_USDT","stocks":0}]
'''
from __future__ import absolute_import, division, print_function
from fmz import * # Import all FMZ functions
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.graphics.api import qqplot
from statsmodels.stats.diagnostic import acorr_ljungbox as lb_test
from scipy import stats
from arch import arch_model
from datetime import timedelta
from itertools import product
from math import sqrt
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error

task = VCtx(__doc__) # Initialization, verification of FMZ reading of historical data
print(exchange.GetAccount())

Keluar[1]: {Balanse: 10000.0, FrozenBalance: 0.0, Stock: 0.0, FrozenStock: 0.0}

    #### Encapsulate some of the functions, which will be used later. If there is a source, see the note

Di [17]:

# Plot functions
def tsplot(y, y_2, lags=None, title='', figsize=(18, 8)):  # source code: https://tomaugspurger.github.io/modern-7-timeseries.html
    fig = plt.figure(figsize=figsize)
    layout = (2, 2)
    ts_ax   = plt.subplot2grid(layout, (0, 0))
    ts2_ax = plt.subplot2grid(layout, (0, 1))
    acf_ax  = plt.subplot2grid(layout, (1, 0))
    pacf_ax = plt.subplot2grid(layout, (1, 1))
    y.plot(ax=ts_ax)
    ts_ax.set_title(title)
    y_2.plot(ax=ts2_ax)
    smt.graphics.plot_acf(y, lags=lags, ax=acf_ax)
    smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax)
    [ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
    sns.despine()
    plt.tight_layout()
    return ts_ax, ts2_ax, acf_ax, pacf_ax

# Performance evaluation
def get_rmse(y, y_hat):
    mse = np.mean((y - y_hat)**2)
    return np.sqrt(mse)

def get_mape(y, y_hat):
    perc_err = (100*(y - y_hat))/y
    return np.mean(abs(perc_err))

def get_mase(y, y_hat):
    abs_err = abs(y - y_hat)
    dsum=sum(abs(y[1:] - y_hat[1:]))
    t = len(y)
    denom = (1/(t - 1))* dsum
    return np.mean(abs_err/denom)

def mae(observation, forecast):    
    error = mean_absolute_error(observation, forecast)
    print('Mean Absolute Error (MAE): {:.3g}'.format(error))
    return error

def mape(observation, forecast): 
    observation, forecast = np.array(observation), np.array(forecast)
    # Might encounter division by zero error when observation is zero
    error = np.mean(np.abs((observation - forecast) / observation)) * 100
    print('Mean Absolute Percentage Error (MAPE): {:.3g}'.format(error))
    return error

def rmse(observation, forecast):
    error = sqrt(mean_squared_error(observation, forecast))
    print('Root Mean Square Error (RMSE): {:.3g}'.format(error))
    return error

def evaluate(pd_dataframe, observation, forecast):
    first_valid_date = pd_dataframe[forecast].first_valid_index()
    mae_error = mae(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    mape_error = mape(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    rmse_error = rmse(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ]) 

    ax = pd_dataframe.loc[:, [observation, forecast]].plot(figsize=(18,5))
    ax.xaxis.label.set_visible(False)
    return

1-2 Mari kita mulai dengan pemahaman singkat tentang data historis Bitcoin

Dari sudut pandang statistik, kita dapat melihat beberapa karakteristik data Bitcoin. Mengambil deskripsi data tahun lalu sebagai contoh, tingkat pengembalian dihitung dengan cara yang sederhana, yaitu harga penutupan dikurangi logaritmik. Rumusnya adalah sebagai berikut: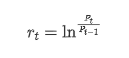

Dalam [3]:

df = get_bars('huobi.btc_usdt', '1d', count=10000, start='2019-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
mean = btc_year_test.mean()
std = btc_year_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value'], columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% btc_year_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% btc_year_test.kurt())
normal_result

Keluar[3]: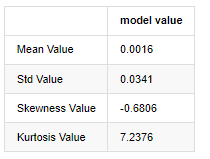

Fitur ekor lemak tebal adalah bahwa semakin pendek skala waktu, semakin signifikan fiturnya. kurtosis akan meningkat dengan peningkatan frekuensi data, dan fitur akan sangat jelas dalam data frekuensi tinggi.

Mengambil data harga penutupan harian dari 1 Januari 2019 hingga saat ini sebagai contoh, kami membuat analisis deskriptif dari tingkat pengembalian logaritma, dan dapat dilihat bahwa seri tingkat pengembalian sederhana Bitcoin tidak sesuai dengan distribusi normal, dan memiliki karakteristik jelas ekor lemak tebal.

Nilai rata-rata urutan adalah 0.0016, standar deviasi adalah 0.0341, skewness adalah -0.6819, dan kurtosis adalah 7.2243, yang jauh lebih tinggi dari distribusi normal dan memiliki karakteristik ekor lemak tebal. normalitas Bitcoins tingkat pengembalian sederhana diukur dan diuji dengan grafik QQ sebagai berikut:

Dalam [4]:

fig = plt.figure(figsize=(4,4))
ax = fig.add_subplot(111)
fig = qqplot(btc_year_test['log_return'], line='q', ax=ax, fit=True)

Keluar[4]:

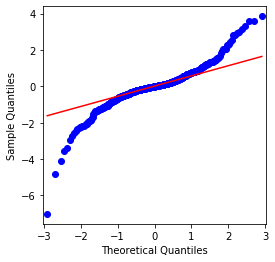
Hal ini dapat dilihat bahwa grafik QQ sempurna, dan deret laba logaritma untuk Bitcoin tidak sesuai dengan distribusi normal dari hasil, dan memiliki karakteristik jelas ekor lemak tebal.

Selanjutnya, mari kita lihat efek agregasi volatilitas, yaitu, deret waktu keuangan sering disertai dengan volatilitas yang lebih besar setelah volatilitas yang lebih besar, sementara volatilitas yang lebih kecil biasanya diikuti oleh volatilitas yang lebih kecil.

Volatility Clustering mencerminkan efek umpan balik positif dan negatif dari volatilitas dan sangat berkorelasi dengan karakteristik buntut lemak. Secara ekonomometri, ini menyiratkan bahwa deret waktu volatilitas mungkin berkorelasi otomatis, yaitu, volatilitas periode saat ini mungkin memiliki beberapa hubungan dengan periode sebelumnya, periode sebelumnya kedua, atau bahkan periode sebelumnya ketiga.

Dalam [5]:

df = get_bars('huobi.btc_usdt', '1d', count=50000, start='2006-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
sns.mpl.rcParams['figure.figsize'] = (18, 4)  # Volatility
ax1 = btc_year_test['log_return'].plot()
ax1.xaxis.label.set_visible(False)

Keluar[5]:

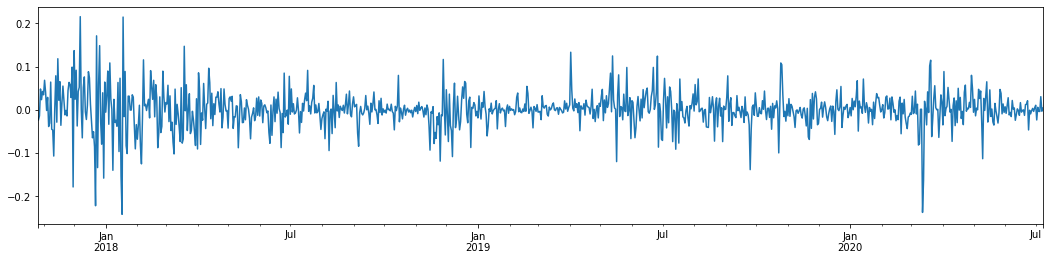
Jika kita mengambil tingkat laba logaritma harian Bitcoin dalam 3 tahun terakhir dan memetakan, fenomena kluster volatilitas dapat dilihat dengan jelas. Setelah pasar bull di Bitcoin pada tahun 2018, itu berada dalam posisi stabil untuk sebagian besar waktu. Seperti yang dapat kita lihat di sebelah kanan, pada bulan Maret 2020, ketika pasar keuangan global jatuh, ada juga lari pada likuiditas Bitcoin, dengan hasil anjlok hampir 40% dalam sehari, dengan perubahan negatif yang tajam.

Dengan kata lain, dari pengamatan intuitif, kita dapat melihat bahwa fluktuasi besar akan diikuti oleh fluktuasi padat dengan probabilitas besar, yang juga merupakan efek agregasi volatilitas.

1-3. Persiapan data

Untuk menyiapkan sampel pelatihan, pertama, kita menetapkan sampel acuan, di mana tingkat pengembalian logaritma adalah volatilitas yang diamati setara. Karena volatilitas hari tidak dapat diamati secara langsung, data per jam digunakan untuk sampel ulang untuk menyimpulkan volatilitas yang direalisasikan hari dan mengambilnya sebagai variabel tergantung dari volatilitas.

Metode pengambilan sampel kembali didasarkan pada data per jam. Rumusnya ditunjukkan sebagai berikut: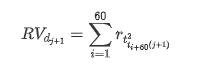

Dalam [4]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_all = pd.DataFrame(df['close'], dtype=np.float)
kline_all.index.name = 'date'
kline_all['log_price'] = np.log(kline_all['close'])  # Calculate daily logarithmic rate of return
kline_all['return'] = kline_all['log_price'].pct_change().dropna()
kline_all['log_return'] = kline_all['log_price'] - kline_all['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_all['squared_log_return'] = np.power(kline_all['log_return'], 2)  # The exponential square of logarithmic daily rate of return

kline_all['return_100x'] = np.multiply(kline_all['return'], 100)
kline_all['log_return_100x'] = np.multiply(kline_all['log_return'], 100)  # Enlarge 100 times

kline_all['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy()  # Resampling to days
kline_all['realized_volatility_1_hour'] = np.sqrt(kline_all['realized_variance_1_hour'])  # Volatility of variance derivation

kline_all = kline_all[4:-29] # Remove the last line because it is missing
kline_all.head(3)

Keluar[4]: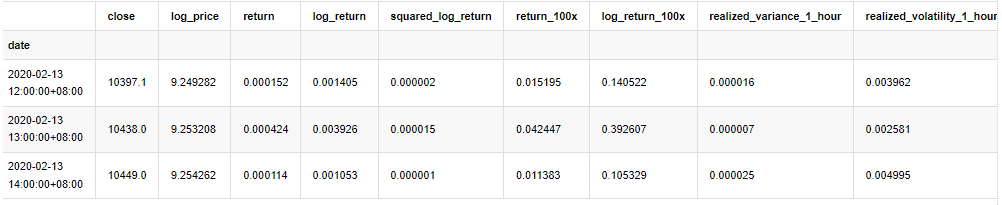

Siapkan data di luar sampel dengan cara yang sama

Dalam [5]:

# Prepare the data outside the sample with realized daily volatility
df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times
kline_1m['squared_log_return'] = np.power(kline_1m['log_return_100x'], 2)
kline_1m#.tail()
df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate daily logarithmic rate of return
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times
kline_test['squared_log_return'] = np.power(kline_test['log_return_100x'], 2)  # The exponential square of logarithmic daily rate of return
kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum()  # Resampling to days
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation
kline_test = kline_test[4:-2]

Untuk memahami data dasar sampel, analisis deskriptif sederhana dilakukan sebagai berikut:

Dalam [9]:

line_test = pd.DataFrame(kline_train['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'

mean = line_test.mean()  # Calculate mean value and standard deviation
std = line_test.std()

line_test.sort_values(by = 'log_return', inplace = True)  # Resort
s_r = line_test.reset_index(drop = False)  # After resorting, update index
s_r['p'] = (s_r.index - 0.5) / len(s_r)  # Calculate the percentile p(i)
s_r['q'] = (s_r['log_return'] - mean) / std  # Calculate the value of q

st = line_test.describe()
x1 ,y1 = 0.25, st['log_return']['25%']
x2 ,y2 = 0.75, st['log_return']['75%']

fig = plt.figure(figsize = (18,8))
layout = (2, 2)
ax1 = plt.subplot2grid(layout, (0, 0), colspan=2)# Plot the data distribution
ax2 = plt.subplot2grid(layout, (1, 0))# Plot histogram
ax3 = plt.subplot2grid(layout, (1, 1))# Draw the QQ chart, the straight line is the connection of the quarter digit, three-quarters digit, which is basically conforms to the normal distribution

ax1.scatter(line_test.index, line_test.values)
line_test.hist(bins=30,alpha = 0.5,ax = ax2)
line_test.plot(kind = 'kde', secondary_y=True,ax = ax2)
ax3.plot(s_r['p'],s_r['log_return'],'k.',alpha = 0.1)
ax3.plot([x1,x2],[y1,y2],'-r')
sns.despine()
plt.tight_layout()

Keluar[9]:

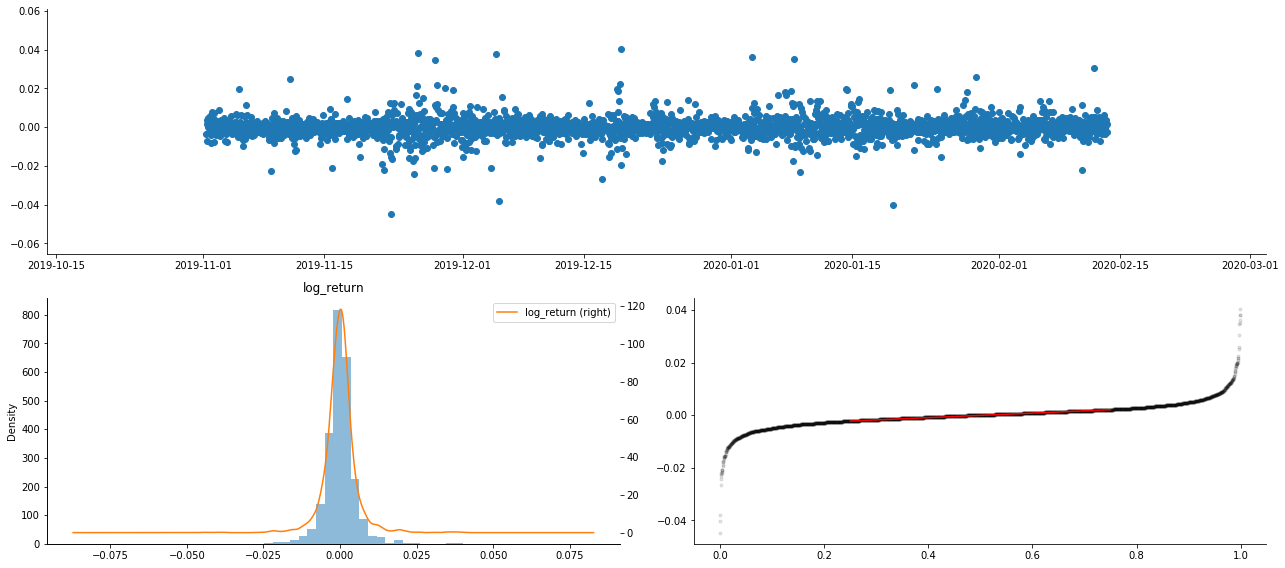
Akibatnya, ada agregasi volatilitas yang jelas dan efek leverage dalam grafik deret waktu laba logaritma.

Ketidakseimbangan dalam grafik distribusi hasil logaritma kurang dari 0, menunjukkan bahwa hasil dalam sampel sedikit negatif dan bias ke kanan.

Ketidaksetaraan distribusi data kurang dari 1, menunjukkan bahwa hasil dalam sampel sedikit positif dan sedikit bias kanan. nilai kurtosis lebih besar dari 3, menunjukkan bahwa hasil adalah ekor lemak tebal didistribusikan.

Sekarang kita telah mencapai titik ini, mari kita lakukan tes statistik lain. Dalam [7]:

line_test = pd.DataFrame(kline_all['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'
mean = line_test.mean()
std = line_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value',
                                    'Ks Test Value','Ks Test P-value',
                                    'Jarque Bera Test','Jarque Bera Test P-value'],
                    columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% line_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% line_test.kurt())
normal_result['model value']['Ks Test Value'] = stats.kstest(line_test, 'norm', (mean, std))[0]
normal_result['model value']['Ks Test P-value'] = stats.kstest(line_test, 'norm', (mean, std))[1]
normal_result['model value']['Jarque Bera Test'] = stats.jarque_bera(line_test)[0]
normal_result['model value']['Jarque Bera Test P-value'] = stats.jarque_bera(line_test)[1]
normal_result

Keluar[7]:

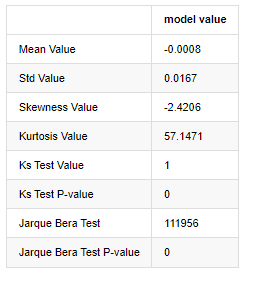
Statistik tes Kolmogorov-Smirnov dan Jarque-Bera digunakan masing-masing. Hipotesis asli ditandai dengan perbedaan signifikan dan distribusi normal. Jika nilai P kurang dari nilai kritis tingkat kepercayaan 0,05%, hipotesis asli ditolak.

Hal ini dapat dilihat bahwa nilai kurtosis lebih besar dari 3, menunjukkan karakteristik ekor lemak tebal. Nilai P dari KS dan JB kurang dari interval kepercayaan. Asumsi distribusi normal ditolak, yang membuktikan bahwa tingkat pengembalian BTC tidak memiliki karakteristik distribusi normal, dan studi empiris memiliki karakteristik ekor lemak tebal.

Perbandingan volatilitas yang direalisasikan dan volatilitas yang diamati

Kami menggabungkan square_log_ return (logaritma hasil kuadrat) dan realized_variance (varians direalisasikan) untuk pengamatan.

Dalam [11]:

fig, ax = plt.subplots(figsize=(18, 6))
start = '2020-03-08 00:00:00+08:00'
end = '2020-03-20 00:00:00+08:00'

np.abs(kline_all['squared_log_return']).loc[start:end].plot(ax=ax,label='squared log return')
kline_all['realized_variance_1_hour'].loc[start:end].plot(ax=ax,label='realized variance')
plt.legend(loc='best')

Keluar[11]:

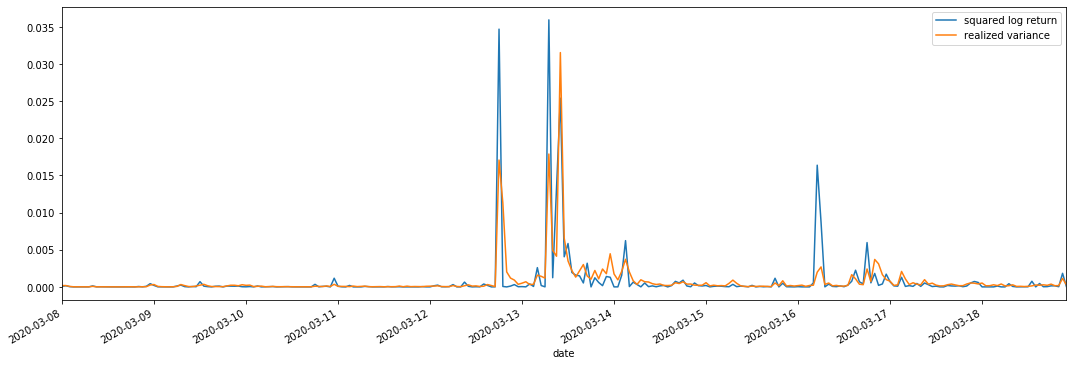
Hal ini dapat dilihat bahwa ketika rentang varians yang direalisasikan lebih besar, volatilitas rentang tingkat pengembalian juga lebih besar, dan tingkat pengembalian yang direalisasikan lebih halus.

Dari sudut pandang murni teoritis, RV lebih dekat dengan volatilitas nyata, sementara volatilitas jangka pendek dihaluskan karena volatilitas intraday milik data overnight, jadi dari sudut pandang observasi, volatilitas intraday lebih cocok untuk frekuensi rendah volatilitas pasar saham.

2. Kerataan deret waktu

Jika ini adalah deret non-stasioner, maka harus disesuaikan dengan deret stasioner. Cara umum adalah dengan melakukan pengolahan perbedaan. Secara teoritis, setelah banyak kali perbedaan, deret non-stasioner dapat didekati dengan deret stasioner. Jika kovarian seri sampel stabil, harapan, varians dan kovarian pengamatan tidak akan berubah seiring waktu, menunjukkan bahwa deret sampel lebih nyaman untuk inferensi dalam analisis statistik.

Uji akar satuan, yaitu uji ADF, digunakan di sini. Uji ADF menggunakan uji t untuk mengamati signifikansi. Pada prinsipnya, jika deret tidak menunjukkan tren yang jelas, hanya item konstan yang dipertahankan. Jika deret memiliki tren, persamaan regresi harus mencakup item konstan dan item tren waktu. Selain itu, kriteria AIC dan BIC dapat digunakan untuk evaluasi berdasarkan kriteria informasi. Jika rumus diperlukan, adalah sebagai berikut: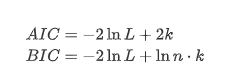

Dalam [8]:

stable_test = kline_all['log_return']
adftest = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='AIC')
adftest2 = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='BIC')
output=pd.DataFrame(index=['ADF Statistic Test Value', "ADF P-value", "Lags", "Number of Observations",
                           "Critical Value(1%)","Critical Value(5%)","Critical Value(10%)"],
                    columns=['AIC','BIC'])
output['AIC']['ADF Statistic Test Value'] = adftest[0]
output['AIC']['ADF P-value'] = adftest[1]
output['AIC']['Lags'] = adftest[2]
output['AIC']['Number of Observations'] = adftest[3]
output['AIC']['Critical Value(1%)'] = adftest[4]['1%']
output['AIC']['Critical Value(5%)'] = adftest[4]['5%']
output['AIC']['Critical Value(10%)'] = adftest[4]['10%']
output['BIC']['ADF Statistic Test Value'] = adftest2[0]
output['BIC']['ADF P-value'] = adftest2[1]
output['BIC']['Lags'] = adftest2[2]
output['BIC']['Number of Observations'] = adftest2[3]
output['BIC']['Critical Value(1%)'] = adftest2[4]['1%']
output['BIC']['Critical Value(5%)'] = adftest2[4]['5%']
output['BIC']['Critical Value(10%)'] = adftest2[4]['10%']
output

Keluar[8]: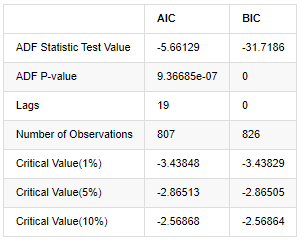

Asumsi asli adalah bahwa tidak ada unit akar dalam deret, yaitu, asumsi alternatif adalah bahwa deret ini statis. nilai P tes jauh lebih kecil dari 0,05% tingkat kepercayaan nilai cut-off, menolak asumsi asli, sehingga log rate of return adalah deret statis, dapat dimodelkan dengan menggunakan model deret waktu statistik.

3. Identifikasi model dan penentuan pesanan

Untuk menetapkan persamaan nilai rata-rata, perlu melakukan uji korélasi otomatis pada urutan untuk memastikan bahwa istilah kesalahan tidak memiliki korélasi otomatis. Pertama, cobalah untuk memetakan korélasi otomatis ACF dan korélasi parsial PACF sebagai berikut:

Dalam [19]:

tsplot(kline_all['log_return'], kline_all['log_return'], title='Log Return', lags=100)

Keluar[19]:

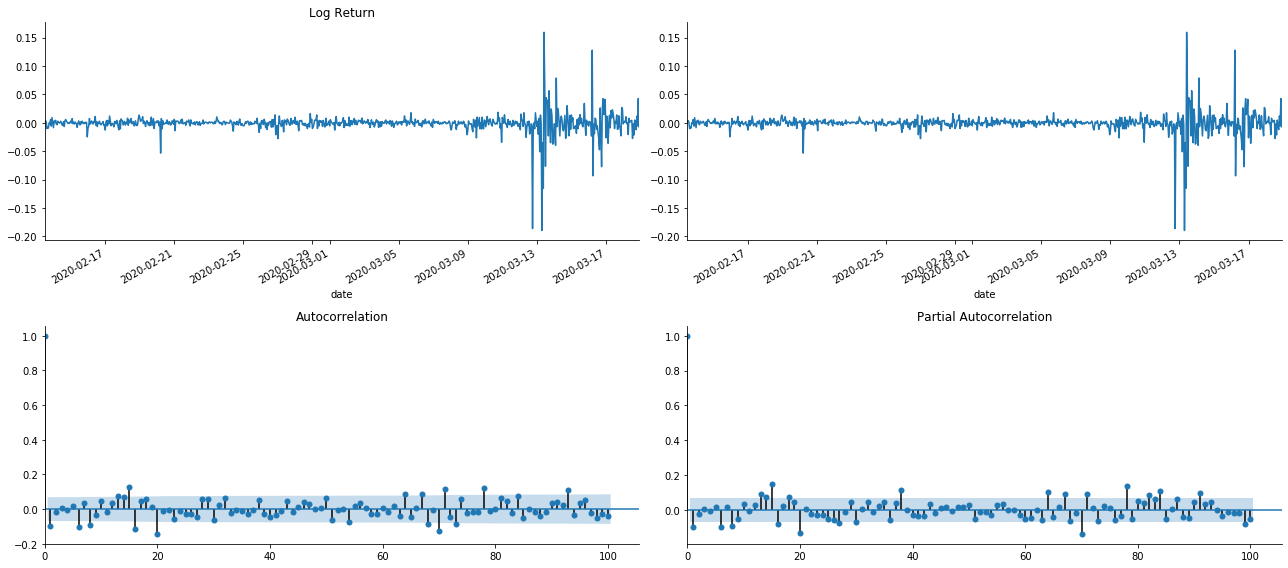
Anda dapat melihat bahwa efek truncasi sempurna. Pada saat itu, gambar ini memberi saya inspirasi. Apakah pasar benar-benar tidak valid? Untuk memverifikasi, kita akan melakukan analisis autocorrelation pada seri pengembalian dan menentukan urutan lag dari model.

Koefisien korelasi yang umum digunakan adalah untuk mengukur korelasi antara itu dan dirinya sendiri, yaitu korelasi antara r ((t) dan r (t-l) pada waktu tertentu di masa lalu: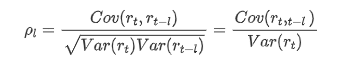

Kemudian mari kita lakukan tes kuantitatif. Asumsi asli adalah bahwa semua koefisien autocorrelation adalah 0, yaitu, tidak ada autocorrelation dalam deret. Rumus statistik tes ditulis sebagai berikut: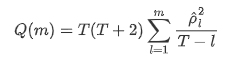

Sepuluh koefisien autocorrelation diambil untuk analisis, sebagai berikut:

Dalam [9]:

acf,q,p = sm.tsa.acf(kline_all['log_return'], nlags=15,unbiased=True,qstat = True, fft=False)  # Test 10 autocorrelation coefficients
output = pd.DataFrame(np.c_[range(1,16), acf[1:], q, p], columns=['lag', 'ACF', 'Q', 'P-value'])
output = output.set_index('lag')
output

Keluar[9]: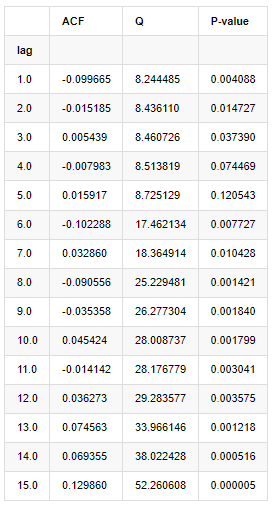

Menurut statistik uji Q dan nilai P, kita dapat melihat bahwa fungsi autocorrelation ACF secara bertahap menjadi 0 setelah urutan 0. Nilai-nilai P dari statistik uji Q cukup kecil untuk menolak asumsi asli, sehingga ada autocorrelation dalam deret.

4. pemodelan ARMA

Model AR dan MA cukup sederhana. Secara sederhana, Markdown terlalu lelah untuk menulis rumus. Jika Anda tertarik, silakan periksa sendiri. Model AR (Autoregression) terutama digunakan untuk memodelkan deret waktu. Jika deret telah lulus tes ACF, yaitu, koefisien korélasi otomatis dengan interval 1 signifikan, yaitu, data pada waktu mungkin berguna untuk memprediksi waktu t.

Model MA (Media Gerak) menggunakan interferensi acak atau prediksi kesalahan dari periode q yang lalu untuk mengekspresikan nilai prediksi saat ini secara linier.

Untuk secara lengkap menggambarkan struktur dinamis data, perlu untuk meningkatkan urutan model AR atau MA, tetapi parameter tersebut akan membuat perhitungan lebih kompleks. Oleh karena itu, untuk menyederhanakan proses ini, model rata-rata bergerak autoregressive (ARMA) diusulkan.

Karena seri waktu harga umumnya tidak stasioner, dan efek optimasi metode perbedaan pada stasioner telah dibahas sebelumnya, model ARIMA (p, d, q) (sum autoregressive moving average) menambahkan pemrosesan perbedaan d-order berdasarkan penerapan model yang ada untuk seri.

Dengan kata lain, satu-satunya perbedaan antara model ARIMA dan proses pembuatan model ARMA adalah bahwa jika hasil yang tidak stabil diperoleh setelah menganalisis stabilitas, model akan membuat perbedaan kuadrat ke seri secara langsung dan kemudian melakukan tes stabilitas, dan kemudian menentukan urutan p dan q sampai seri stabil. Setelah membangun model dan mengevaluasinya, prediksi berikutnya akan dibuat, menghilangkan langkah kembali untuk melakukan perbedaan. Namun, perbedaan harga urutan kedua tidak berarti, jadi ARMA adalah pilihan terbaik.

Pemilihan pesanan

Selanjutnya, kita dapat memilih urutan langsung dengan kriteria informasi, di sini kita mencoba dengan diagram termodinamika dari AIC dan BIC.

Dalam [10]:

def select_best_params():
    ps = range(0, 4)
    ds= range(1, 2)
    qs = range(0, 4)
    parameters = product(ps, ds, qs)
    parameters_list = list(parameters)

    p_min = 0
    d_min = 0
    q_min = 0
    p_max = 3
    d_max = 3
    q_max = 3

    results_aic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    results_bic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    
    best_params = []
    aic_results = []
    bic_results = []
    hqic_results = []
    best_aic = float("inf")
    best_bic = float("inf")
    best_hqic = float("inf")
    warnings.filterwarnings('ignore')
    for param in parameters_list:
        try:
            model = sm.tsa.SARIMAX(kline_all['log_price'], order=(param[0], param[1], param[2])).fit(disp=-1)
            results_aic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.aic
            results_bic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.bic
        except ValueError:
            continue    
           
        aic_results.append([param, model.aic])
        bic_results.append([param, model.bic])
        hqic_results.append([param, model.hqic])
    
    results_aic = results_aic[results_aic.columns].astype(float)
    results_bic = results_bic[results_bic.columns].astype(float)
    
    # Draw thermodynamic diagrams of AIC and BIC to find the best
    fig = plt.figure(figsize=(18, 9))
    layout = (2, 2)
    aic_ax = plt.subplot2grid(layout, (0, 0))
    bic_ax = plt.subplot2grid(layout, (0, 1))

    aic_ax = sns.heatmap(results_aic,mask=results_aic.isnull(),ax=aic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    aic_ax.set_title('AIC');
    bic_ax = sns.heatmap(results_bic,mask=results_bic.isnull(),ax=bic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    bic_ax.set_title('BIC');
    
    aic_df = pd.DataFrame(aic_results)
    aic_df.columns = ['params', 'aic']   
    best_params.append(aic_df.params[aic_df.aic.idxmin()])
    print('AIC best param: {}'.format(aic_df.params[aic_df.aic.idxmin()]))
    
    bic_df = pd.DataFrame(bic_results)
    bic_df.columns = ['params', 'bic']
    best_params.append(bic_df.params[bic_df.bic.idxmin()])
    print('BIC best param: {}'.format(bic_df.params[bic_df.bic.idxmin()]))
    
    hqic_df = pd.DataFrame(hqic_results)
    hqic_df.columns = ['params', 'hqic']
    best_params.append(hqic_df.params[hqic_df.hqic.idxmin()])
    print('HQIC best param: {}'.format(hqic_df.params[hqic_df.hqic.idxmin()]))

    for best_param in best_params:
        if best_params.count(best_param)>=2:
            print('Best Param Selected: {}'.format(best_param))
            return best_param 

best_param = select_best_params()

Keluar[10]: Param AIC terbaik: (0, 1, 1) Param BIC terbaik: (0, 1, 1) HQIC param terbaik: (0, 1, 1) Param Terbaik Dipilih: (0, 1, 1)

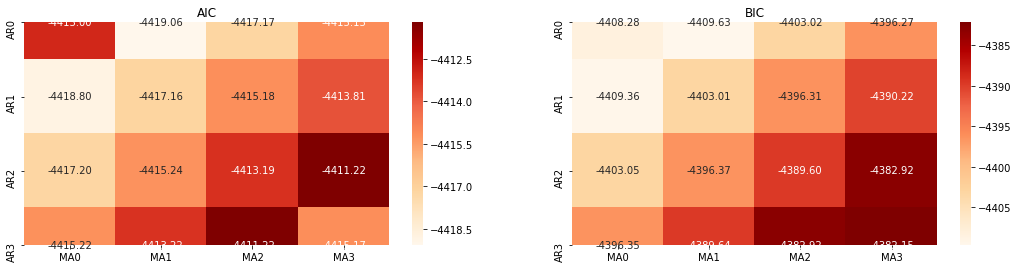
Ini jelas bahwa kombinasi parameter orde pertama yang optimal untuk harga logaritma adalah (0,1,1), yang sederhana dan mudah. log_return (tingkat pengembalian logaritma) melakukan operasi yang sama. Nilai optimal AIC adalah (4,3), dan nilai optimal BIC adalah (0,1). Jadi kombinasi parameter optimal untuk log_return (tingkat pengembalian logaritma) adalah (0,1).

4-2. pemodelan dan pencocokan ARMA

Koefisien kuartal tidak diperlukan, tetapi SARIMAX lebih kaya atribut, jadi diputuskan untuk memilih model ini untuk pemodelan dan secara kebetulan membuat analisis deskriptif sebagai berikut:

Dalam [11]:

params = (0, 0, 1)
training_model = smt.SARIMAX(endog=kline_all['log_return'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
model_results = training_model.fit(disp=False)
model_results.summary()

Keluar[11]: Hasil Model Ruang Negara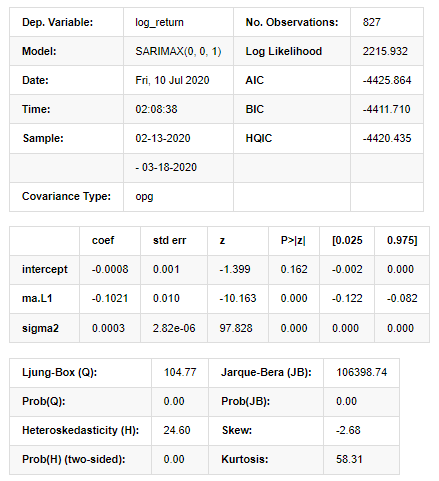

Peringatan: [1] Matriks kovarians dihitung dengan menggunakan produk luar gradien (langkah kompleks). Dalam [27]:

model_results.plot_diagnostics(figsize=(18, 10));

Keluar[27]:

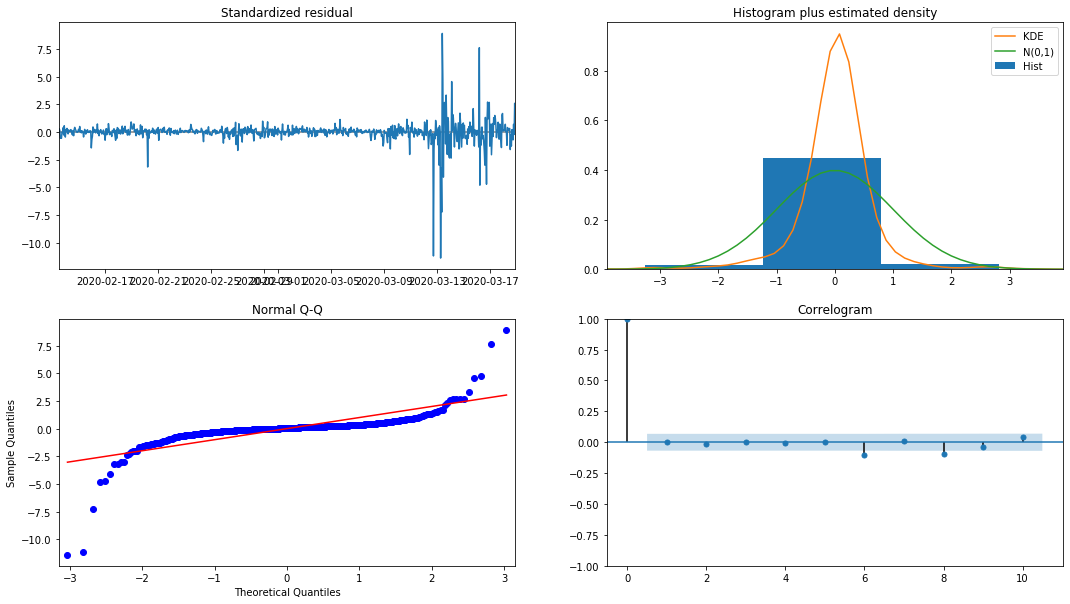
Ketumpatan probabilitas KDE dalam histogram jauh dari distribusi normal N (0,1), yang menunjukkan bahwa residual bukanlah distribusi normal. Dalam plot kuantil QQ, residual sampel yang disampel dari distribusi normal standar tidak sepenuhnya mengikuti tren linier, sehingga dikonfirmasi lagi bahwa residual bukan distribusi normal dan lebih dekat dengan white noise.

Kemudian, setelah mengatakan itu, apakah model dapat digunakan masih perlu diuji.

4-3. pengujian model

Efek pencocokan residual tidak ideal, jadi kami melakukan tes Durbin Watson di atasnya. Hipotesis asli tes adalah bahwa urutan tidak memiliki auto-korrelasi, dan urutan hipotesis alternatif tidak bergerak. Selain itu, jika nilai P dari tes LB, JB dan H kurang dari nilai kritis tingkat kepercayaan 0,05%, hipotesis asli akan ditolak.

Dalam [12]:

het_method='breakvar'
norm_method='jarquebera'
sercor_method='ljungbox'

(het_stat, het_p) = model_results.test_heteroskedasticity(het_method)[0]
norm_stat, norm_p, skew, kurtosis = model_results.test_normality(norm_method)[0]

sercor_stat, sercor_p = model_results.test_serial_correlation(method=sercor_method)[0]
sercor_stat = sercor_stat[-1] # The last value of the maximum period
sercor_p = sercor_p[-1]

dw = sm.stats.stattools.durbin_watson(model_results.filter_results.standardized_forecasts_error[0, model_results.loglikelihood_burn:])

arroots_outside_unit_circle = np.all(np.abs(model_results.arroots) > 1)
maroots_outside_unit_circle = np.all(np.abs(model_results.maroots) > 1)

print('Test heteroskedasticity of residuals ({}): stat={:.3f}, p={:.3f}'.format(het_method, het_stat, het_p));
print('\nTest normality of residuals ({}): stat={:.3f}, p={:.3f}'.format(norm_method, norm_stat, norm_p));
print('\nTest serial correlation of residuals ({}): stat={:.3f}, p={:.3f}'.format(sercor_method, sercor_stat, sercor_p));
print('\nDurbin-Watson test on residuals: d={:.2f}\n\t(NB: 2 means no serial correlation, 0=pos, 4=neg)'.format(dw))
print('\nTest for all AR roots outside unit circle (>1): {}'.format(arroots_outside_unit_circle))
print('\nTest for all MA roots outside unit circle (>1): {}'.format(maroots_outside_unit_circle))

root_test=pd.DataFrame(index=['Durbin-Watson test on residuals','Test for all AR roots outside unit circle (>1)','Test for all MA roots outside unit circle (>1)'],columns=['c'])
root_test['c']['Durbin-Watson test on residuals']=dw
root_test['c']['Test for all AR roots outside unit circle (>1)']=arroots_outside_unit_circle
root_test['c']['Test for all MA roots outside unit circle (>1)']=maroots_outside_unit_circle
root_test

Keluar[12]: Tes heteroskedastikitas residu (breakvar): stat=24,598, p=0.000

Normalitas tes residu (jarquebera): stat=106398.739, p=0.000

Korélasi seri residu uji (ljungbox): stat=104.767, p=0.000

Tes Durbin-Watson pada residu: d=2,00 (NB: 2 berarti tidak ada korelasi serial, 0=pos, 4=negatif)

Uji untuk semua akar AR di luar lingkaran satuan (>1): Benar

Uji untuk semua akar MA di luar lingkaran satuan (>1): Benar

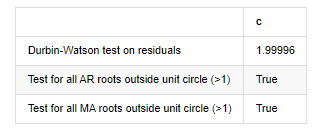
Di [13]:

kline_all['log_price_dif1'] = kline_all['log_price'].diff(1)
kline_all = kline_all[1:]
kline_train = kline_all

training_label = 'log_return'
training_ts = pd.DataFrame(kline_train[training_label], dtype=np.float)

delta = model_results.fittedvalues - training_ts[training_label]
adjR = 1 - delta.var()/training_ts[training_label].var()
adjR_test=pd.DataFrame(index=['adjR2'],columns=['Value'])
adjR_test['Value']['adjR2']=adjR**2
adjR_test

Keluar[13]:

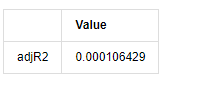
Jika statistik uji Durbin Watson sama dengan 2, mengkonfirmasi bahwa deret tidak memiliki korelasi, dan nilai statistiknya didistribusikan antara (0,4). Dekat dengan 0 berarti korelasi positif tinggi, sedangkan dekat dengan 4 berarti korelasi negatif tinggi. Di sini kira-kira sama dengan 2. Nilai P dari tes lain cukup kecil, akar karakteristik satuan berada di luar lingkaran satuan, dan semakin besar nilai dari adjR2 yang dimodifikasi, semakin baik hasilnya. Hasil keseluruhan dari pengukuran tampaknya tidak memuaskan.

Dalam [14]:

model_results.params

Keluar[14]: Mencegat -0.000817 ma.L1 -0.102102 Sigma2 0,000275 djenis: float64

Singkatnya, parameter pengaturan urutan ini pada dasarnya dapat memenuhi persyaratan pemodelan deret waktu dan pemodelan volatilitas berikutnya, tetapi efek pencocokan adalah seperti ini.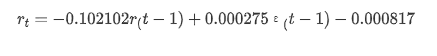

4-4. prediksi model

Selanjutnya, model terlatih dicocokkan ke depan. statsmodels menyediakan opsi statis dan dinamis untuk pencocokan dan peramalan. Perbedaannya terletak pada apakah nilai observasi digunakan dalam langkah berikutnya dari peramalan, atau nilai prediksi yang dihasilkan dalam langkah sebelumnya digunakan secara iteratif.

Di [37]:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=False)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Keluar[37]:

Hal ini dapat dilihat bahwa efek pas dari mode statis pada sampel sangat baik, data sampel dapat hampir ditutupi oleh 95% interval konfidensi, dan mode dinamis sedikit tidak terkendali.

Jadi mari kita lihat efek pencocokan data dalam modus dinamis:

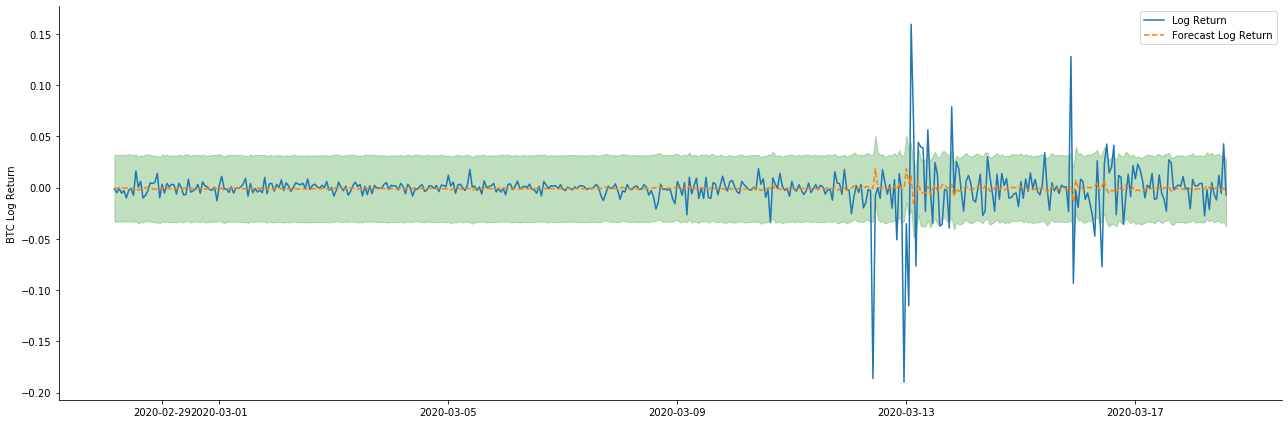
Di [38]:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=True)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Keluar[38]:

Hal ini dapat dilihat bahwa efek pas dari kedua model pada sampel sangat baik, dan nilai rata-rata dapat hampir ditutupi oleh 95% confidence interval, tetapi model statis jelas lebih cocok.

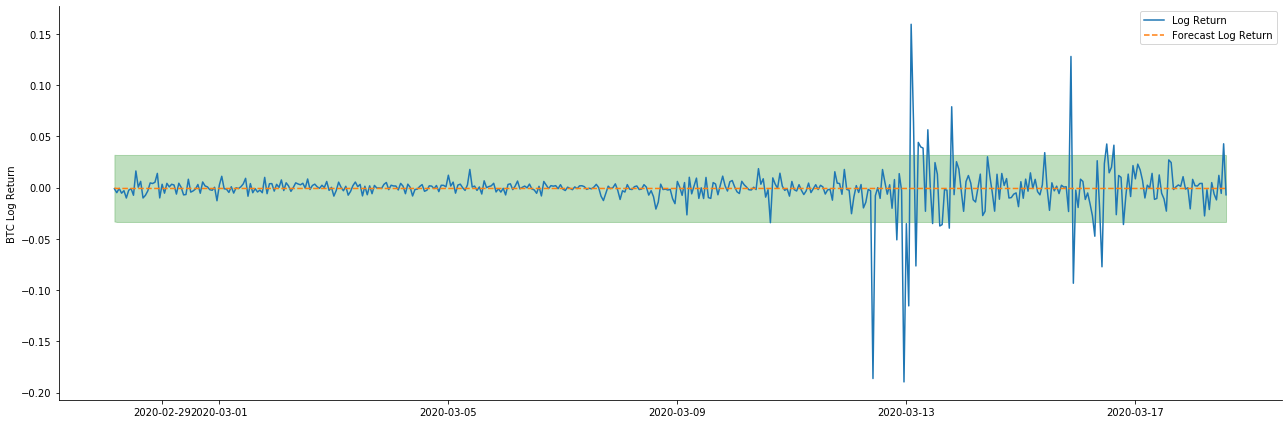
Dalam [41]:

# Out-of-sample predicted data predict()
start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-20 23:00:00+08:00'
model = False

predict_step = 50
predicts_ARIMA_normal = model_results.get_prediction(start=start_date, dynamic=model, full_reports=True)
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:]

predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=model)
ci_normal_out = predicts_ARIMA_normal_out.conf_int().loc[start_date:end_date]

fig, ax = plt.subplots(figsize=(18,8))
kline_test.loc[start_date:end_date, 'log_return'].plot(ax=ax, label='Benchmark Log Return')

predicts_ARIMA_normal.predicted_mean.plot(ax=ax, style='g', label='In Sample Forecast')
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='g', alpha=0.1)

predicts_ARIMA_normal_out.predicted_mean.loc[:end_date].plot(ax=ax, style='r--', label='Out of Sample Forecast')
ax.fill_between(ci_normal_out.index, ci_normal_out.iloc[:,0], ci_normal_out.iloc[:,1], color='r', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

Keluar[41]:

Karena pencocokan data dalam sampel adalah prediksi maju yang bergulir, ketika jumlah informasi dalam sampel cukup, model statis rentan terhadap pencocokan yang berlebihan, sementara model dinamis tidak memiliki variabel dependen yang dapat diandalkan, dan efeknya menjadi semakin buruk setelah iterasi.

Jika kita membalikkan ramalan tingkat pengembalian ke log_price (harga logaritma), pencocokan ditunjukkan dalam gambar di bawah ini:

Dalam [42]:

params = (0, 1, 1)
mod = smt.SARIMAX(endog=kline_all['log_price'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
res = mod.fit(disp=False)

start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-15 23:00:00+08:00'

predicts_ARIMA_normal = res.get_prediction(start=start_date, dynamic=False, full_results=False)
predicts_ARIMA_dynamic = res.get_prediction(start=start_date, dynamic=True, full_results=False)

fig, ax = plt.subplots(figsize=(18,6))
kline_test.loc[start_date:end_date, 'log_price'].plot(ax=ax, label='Log Price')

predicts_ARIMA_normal.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='r--', label='Normal Prediction')
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:end_date]
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='r', alpha=0.1)

predicts_ARIMA_dynamic.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='g', label='Dynamic Prediction')
ci_dynamic = predicts_ARIMA_dynamic.conf_int().loc[start_date:end_date]
ax.fill_between(ci_dynamic.index, ci_dynamic.iloc[:,0], ci_dynamic.iloc[:,1], color='g', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

Keluar[42]:

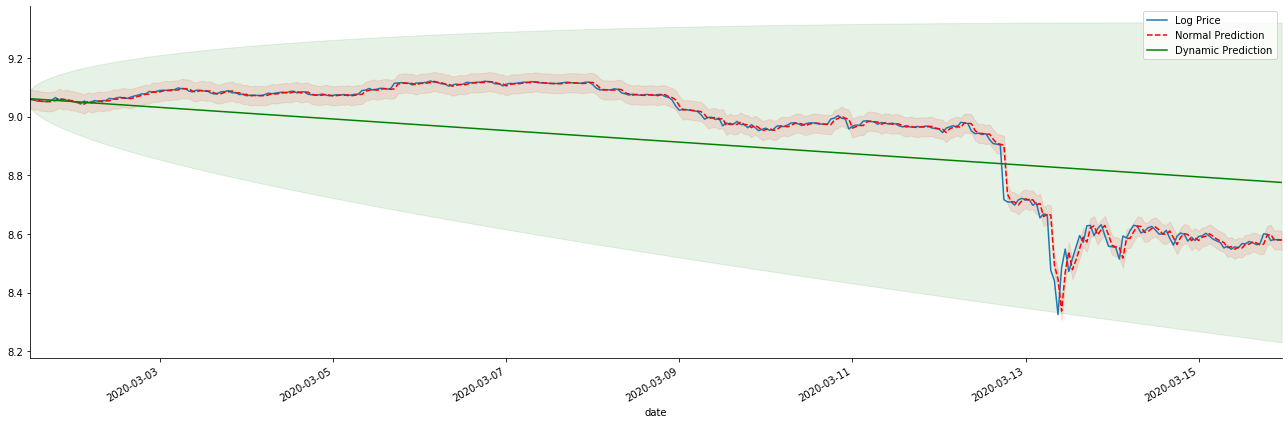
Sangat mudah untuk melihat keuntungan yang cocok dari model statis dan perbedaan ekstrim antara model dinamis dan model statis dalam prediksi jangka panjang. garis bertitik merah dan kisaran merah muda... Anda tidak bisa mengatakan bahwa prediksi model ini salah. Lagi pula, itu mencakup tren rata-rata bergerak sepenuhnya, tapi... apakah itu berarti?

Pada kenyataannya, model ARMA itu sendiri tidak salah, karena masalahnya bukan model itu sendiri, tetapi logika obyektif dari hal-hal itu sendiri. Model deret waktu hanya dapat ditetapkan berdasarkan korelasi antara pengamatan sebelumnya dan berikutnya. Oleh karena itu, tidak mungkin untuk memodelkan deret white noise. Oleh karena itu, semua pekerjaan sebelumnya didasarkan pada asumsi berani bahwa deret tingkat pengembalian BTC tidak dapat independen dan didistribusikan secara identik.

Secara umum, seri tingkat pengembalian adalah seri perbedaan martingale, yang berarti bahwa tingkat pengembalian tidak dapat diprediksi, dan asumsi efisiensi yang lemah dari pasar yang sesuai berlaku.

Namun, urutan residu yang dicocokkan juga merupakan urutan perbedaan martingale. urutan perbedaan martingale mungkin tidak independen dan didistribusikan secara identik, tetapi varians bersyarat mungkin tergantung pada nilai masa lalu, sehingga korélasi otomatis orde pertama hilang, tetapi masih ada korélasi otomatis orde lebih tinggi, yang juga merupakan prasyarat penting untuk volatilitas dimodelkan dan diamati.

Jika logika seperti itu berlaku, maka premis membangun berbagai model volatilitas juga berlaku. jadi untuk seri tingkat pengembalian, jika pasar yang kurang efisien terpenuhi, maka nilai rata-rata harus sulit diprediksi, tetapi variansnya dapat diprediksi. dan ARMA yang dicocokkan memberikan patokan seri waktu berkualitas yang adil, maka kualitas juga menentukan kualitas prediksi volatilitas.

Akhirnya, mari kita menilai efek prediksi dengan sederhana. Dengan kesalahan sebagai patokan evaluasi, indikator di dalam dan di luar sampel adalah sebagai berikut:

Di [15]:

start = '2020-02-14 00:00:00+08:00'
predicts_ARIMA_normal = model_results.get_prediction(dynamic=False)
predicts_ARIMA_dynamic = model_results.get_prediction(dynamic=True)
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [rmse(predicts_ARIMA_normal.predicted_mean[1:], kline_test[training_label][:826]),
                          rmse(predicts_ARIMA_dynamic.predicted_mean[1:], kline_test[training_label][:826])]
compare_ARCH_X['MAPE'] = [mape(predicts_ARIMA_normal.predicted_mean[:50], kline_test[training_label][:50]),
                          mape(predicts_ARIMA_dynamic.predicted_mean[:50], kline_test[training_label][:50])]
compare_ARCH_X

Keluar[15]: Kasalahan akar rata-rata persegi (RMSE): 0,0184 Kasalahan akar rata-rata persegi (RMSE): 0,0167 Kesalahan persentase absolut rata-rata (MAPE): 2,25e+03 Kesalahan persentase absolut rata-rata (MAPE): 395

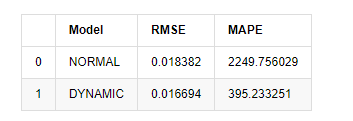
Dilihat bahwa model statis sedikit lebih baik daripada model dinamis dalam hal kesamaan kesalahan antara nilai yang diprediksi dan nilai riil. Ini cocok dengan tingkat pengembalian logaritma Bitcoin dengan baik, yang pada dasarnya sesuai dengan harapan. Prediksi dinamis tidak memiliki informasi variabel yang lebih akurat, dan kesalahan juga diperbesar oleh iterasi, sehingga efek prediksi buruk. MAPE lebih besar dari 100%, sehingga kualitas pencocokan sebenarnya dari kedua model tidak ideal.

Dalam [18]:

predict_step = 50
predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=False)
predicts_ARIMA_dynamic_out = model_results.get_forecast(steps=predict_step, dynamic=True)
testing_ts = kline_test
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [get_rmse(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_rmse(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X['MAPE'] = [get_mape(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_mape(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X

Keluar[18]:

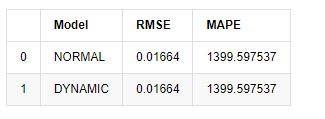
Karena prediksi berikutnya di luar sampel tergantung pada hasil langkah sebelumnya, hanya model dinamis yang efektif. Namun, cacat kesalahan jangka panjang dari model dinamis menyebabkan kemampuan prediksi keseluruhan model tidak cukup, sehingga langkah berikutnya diprediksi paling banyak.

Untuk meringkas, model statis model ARMA cocok untuk mencocokkan tingkat pengembalian intra sampel Bitcoin. Prediksi jangka pendek tingkat pengembalian dapat mencakup interval kepercayaan secara efektif, tetapi prediksi jangka panjang sangat sulit, yang memenuhi efektivitas pasar yang lemah. Setelah pengujian, tingkat pengembalian dalam interval sampel memenuhi premis pengamatan volatilitas berikutnya.

5. efek ARCH

Efek model ARCH adalah korelasi seri dari urutan heteroskedastikitas bersyarat. Tes campuran Ljung Box digunakan untuk menguji korelasi seri persegi residual untuk menentukan apakah ada efek ARCH. Jika tes efek ARCH lulus, yaitu seri memiliki heteroskedastikitas, langkah berikutnya dari pemodelan GARCH dapat dilakukan untuk memperkirakan persamaan rata-rata dan persamaan volatilitas bersama-sama. Jika tidak, model perlu dioptimalkan dan disesuaikan kembali, seperti pemrosesan diferensial atau seri timbal balik.

Kami menyiapkan beberapa set data dan variabel global di sini:

Di [33]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=count_num, start=start_date)  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=count_num, start=start_date)  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate the daily logarithmic rate of return
kline_test['return'] = kline_test['log_price'].pct_change().dropna()
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate the logarithmic rate of return
kline_test['squared_log_return'] = np.power(kline_test['log_return'], 2)  # Exponential square of log daily return rate

kline_test['return_100x'] = np.multiply(kline_test['return'], 100)
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times

kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy() # Resampling to days 
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation

kline_test = kline_test[4:-2500]
kline_test.head(3)

Keluar[33]:

Dalam [22]:

cc = 3
model_p = 1
predict_lag = 30
label = 'log_return'

training_label = label
training_ts = pd.DataFrame(kline_test[training_label], dtype=np.float)

training_arch_label = label
training_arch = pd.DataFrame(kline_test[training_arch_label], dtype=np.float)

training_garch_label = label
training_garch = pd.DataFrame(kline_test[training_garch_label], dtype=np.float)

training_egarch_label = label
training_egarch = pd.DataFrame(kline_test[training_egarch_label], dtype=np.float)

training_arch.plot(figsize = (18,4))

Keluar[22]: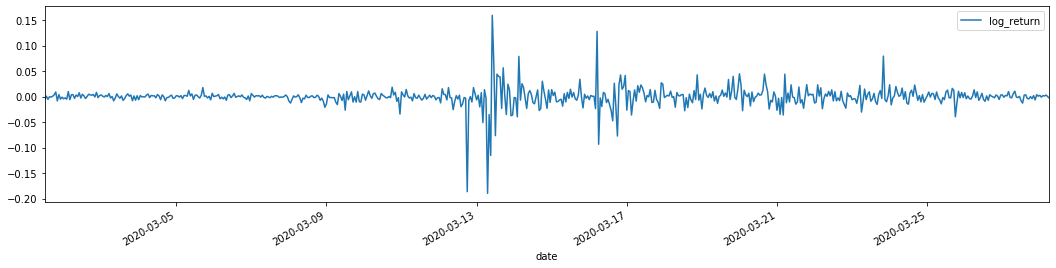

Rasio logaritma dikembalikan ditunjukkan di atas. Selanjutnya, kita perlu menguji efek ARCH dari sampel. Kita menetapkan seri residual dalam sampel berdasarkan ARMA. Beberapa seri dan seri persegi residual dan residual dihitung terlebih dahulu:

Dalam [20]:

training_arma_model = smt.SARIMAX(endog=training_ts, trend='c', order=(0, 0, 1), seasonal_order=(0, 0, 0, 0))
arma_model_results = training_arma_model.fit(disp=False)
arma_model_results.summary()
training_arma_fitvalue = pd.DataFrame(arma_model_results.fittedvalues,dtype=np.float)
at = pd.merge(training_ts, training_arma_fitvalue, on='date')
at.columns = ['log_return', 'model_fit']
at['res'] = at['log_return'] - at['model_fit']
at['res2'] = np.square(at['res'])
at.head()

Keluar[20]:

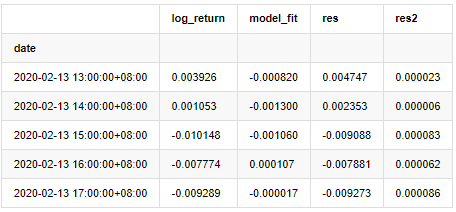
Seri residual sampel kemudian digambarkan

Di [69]:

fig, ax = plt.subplots(figsize=(18, 6))
ax1 = fig.add_subplot(2,1,1)
at['res'][1:].plot(ax=ax1,label='resid')
plt.legend(loc='best')

ax2 = fig.add_subplot(2,1,2)
at['res2'][1:].plot(ax=ax2,label='resid2')

plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Keluar[69]:

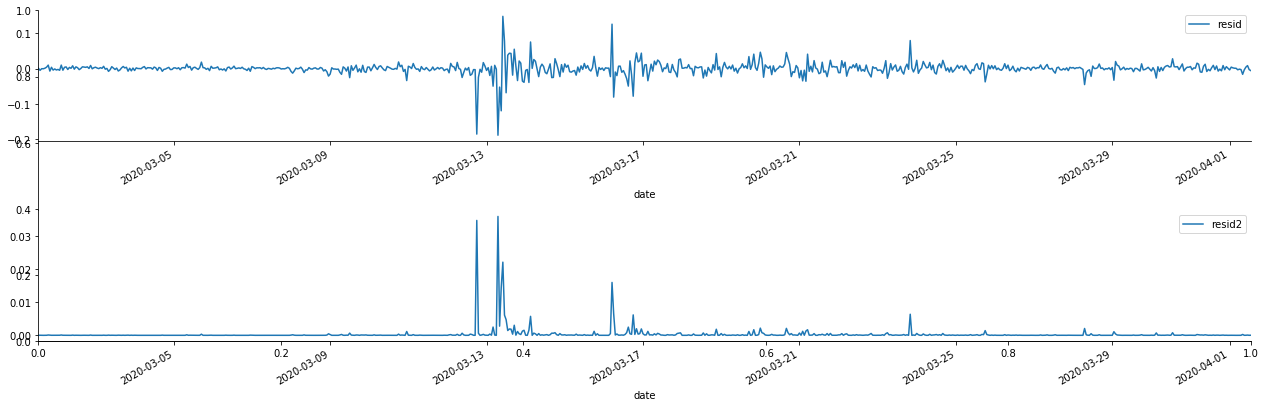
Hal ini dapat dilihat bahwa deret residu memiliki karakteristik agregasi yang jelas, dan dapat dinilai pada awalnya bahwa deret memiliki efek ARCH. ACF juga diambil untuk menguji autocorrelation residu kuadrat, dan hasilnya adalah sebagai berikut.

Dalam [70]:

figure = plt.figure(figsize=(18,4))
ax1 = figure.add_subplot(111)
fig = sm.graphics.tsa.plot_acf(at['res2'],lags = 40, ax=ax1)

Keluar[70]:

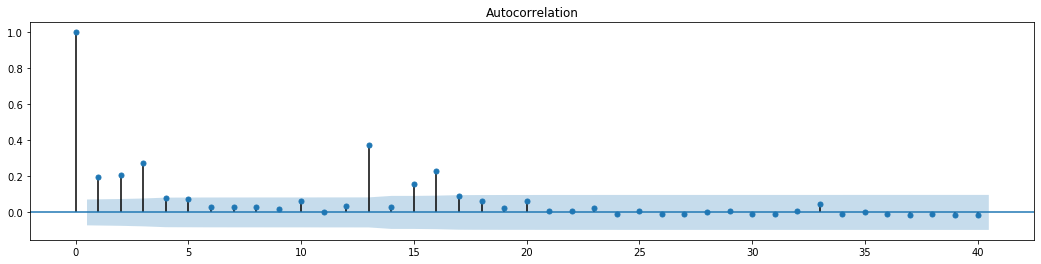
Asumsi awal untuk tes campuran seri adalah bahwa seri tidak memiliki korelasi. Dapat dilihat bahwa nilai P yang sesuai dari 20 urutan data pertama kurang dari nilai kritis dari tingkat kepercayaan 0,05%. Oleh karena itu, asumsi asli ditolak, yaitu residual seri memiliki efek ARCH. Model varians dapat ditetapkan melalui model tipe ARCH untuk menyesuaikan heteroscedasticity dari seri residual dan lebih lanjut memprediksi volatilitas.

6. model GARCH

Sebelum melakukan pemodelan GARCH, kita perlu berurusan dengan bagian ekor lemak dari deret. Karena istilah kesalahan deret dalam hipotesis perlu sesuai dengan distribusi normal atau distribusi t, dan kita sebelumnya telah memverifikasi bahwa deret hasil memiliki distribusi ekor lemak, jadi kita perlu menggambarkan dan melengkapi bagian ini.

Dalam pemodelan GARCH, item kesalahan memberikan pilihan distribusi normal, distribusi t, distribusi GED (Generalized Error Distribution) dan distribusi t Siswa Skewed. Menurut kriteria AIC, kita menggunakan estimasi regresi gabungan penghitungan untuk membandingkan hasil semua pilihan, dan mendapatkan tingkat pencocokan terbaik dari G

Berkaitan

Lebih banyak