Mencapai strategi ekuitas yang seimbang dengan keselarasan yang teratur

Mencapai strategi ekuitas yang seimbang dengan keselarasan yang teratur

Dalam artikel sebelumnya (https://www.fmz.com/bbs-topic/9862), kami memperkenalkan strategi perdagangan pasangan dan menunjukkan bagaimana membuat dan mengotomatiskan strategi perdagangan dengan menggunakan data dan analisis matematis.

Strategi ekuitas seimbang posisi pendek panjang adalah perpanjangan alami dari strategi perdagangan pasangan yang berlaku untuk keranjang objek perdagangan. Hal ini sangat cocok untuk pasar perdagangan dengan banyak varietas dan interrelasi, seperti pasar mata uang digital dan pasar berjangka komoditas.

Prinsip-prinsip dasar

Strategi ekuitas seimbang posisi pendek panjang adalah untuk pergi panjang dan pergi pendek keranjang target perdagangan secara bersamaan. Sama seperti perdagangan pasangan, itu menentukan target investasi mana yang murah dan target investasi mana yang mahal. Perbedaannya adalah bahwa strategi ekuitas seimbang posisi pendek panjang akan mengatur semua target investasi dalam kumpulan pemilihan saham untuk menentukan target investasi mana yang relatif murah atau mahal. Kemudian, itu akan pergi panjang n target investasi teratas berdasarkan peringkat, dan pergi pendek n target investasi terbawah dalam jumlah yang sama (jumlah nilai posisi panjang = total nilai posisi pendek).

Apakah Anda ingat apa yang kami katakan bahwa perdagangan pasangan adalah strategi netral pasar? Hal yang sama berlaku untuk strategi ekuitas yang seimbang posisi pendek panjang, karena jumlah posisi panjang dan pendek yang sama memastikan bahwa strategi akan tetap netral pasar (tidak terpengaruh oleh fluktuasi pasar). Strategi ini juga secara statistik kuat; Dengan peringkat target investasi dan memegang posisi panjang, Anda dapat membuka posisi pada model peringkat Anda berkali-kali, bukan hanya satu kali risiko posisi pembukaan. Anda murni bertaruh pada kualitas skema peringkat Anda.

Apa skema peringkatnya?

Skema peringkat adalah model yang dapat menetapkan prioritas untuk setiap subjek investasi sesuai dengan kinerja yang diharapkan. Faktor-faktor dapat menjadi faktor nilai, indikator teknis, model penetapan harga atau kombinasi dari semua faktor di atas. Misalnya, Anda dapat menggunakan indikator momentum untuk memberi peringkat serangkaian target investasi pelacakan tren: diharapkan bahwa target investasi dengan momentum tertinggi akan terus berkinerja baik dan mendapatkan peringkat tertinggi; Objek investasi dengan momentum terkecil memiliki kinerja terburuk dan pengembalian terendah.

Keberhasilan strategi ini hampir seluruhnya tergantung pada skema peringkat yang digunakan, yaitu, skema peringkat Anda dapat memisahkan target investasi kinerja tinggi dari target investasi kinerja rendah, sehingga dapat lebih mewujudkan pengembalian strategi dari target investasi posisi panjang dan pendek.

Bagaimana membuat skema peringkat?

Setelah kita menentukan skema peringkat, kita berharap untuk mendapatkan keuntungan darinya. Kita melakukan ini dengan menginvestasikan jumlah modal yang sama untuk pergi panjang target investasi atas dan pergi pendek target investasi bawah. Ini memastikan bahwa strategi hanya akan menghasilkan keuntungan yang sebanding dengan kualitas peringkat, dan itu akan neutral pasar.

Misalkan Anda peringkat semua target investasi m, dan Anda memiliki n dolar untuk investasi, dan Anda ingin memegang total 2p (di mana m>2p) posisi.

• Anda peringkat objek investasi sebagai: 1,...,p posisi, pergi pendek target investasi 2/2p USD.

• Anda peringkat objek investasi sebagai: m-p,...,m posisi, pergi panjang target investasi n/2p USD.

Catatan: Karena harga objek investasi yang disebabkan oleh fluktuasi harga tidak akan selalu membagi n/2p secara merata, dan beberapa objek investasi harus dibeli dengan bilangan bulat, akan ada beberapa algoritma yang tidak akurat, yang harus sedekat mungkin dengan angka ini.

n/2p = 100000/1000 = 100

Ini akan menyebabkan masalah besar untuk skor dengan harga lebih besar dari 100 (seperti pasar berjangka komoditas), karena Anda tidak dapat membuka posisi dengan harga pecahan (masalah ini tidak ada di pasar mata uang digital).

Mari kita ambil contoh hipotetis.

• Membangun lingkungan penelitian kami di platform FMZ Quant

Pertama-tama, untuk bekerja dengan lancar, kita perlu membangun lingkungan penelitian kita.FMZ.COM) untuk membangun lingkungan penelitian kami, terutama untuk menggunakan antarmuka API yang nyaman dan cepat dan sistem Docker yang dikemas dengan baik dari platform ini nanti.

Dalam nama resmi platform FMZ Quant, sistem Docker ini disebut sistem Docker.

Silakan lihat artikel saya sebelumnya tentang cara mengimplementasikan docker dan robot:https://www.fmz.com/bbs-topic/9864.

Pembaca yang ingin membeli server komputasi awan mereka sendiri untuk menyebarkan dockers dapat merujuk pada artikel ini:https://www.fmz.com/digest-topic/5711.

Setelah menyebarkan server komputasi awan dan sistem docker dengan sukses, selanjutnya kita akan menginstal artefak terbesar saat ini Python: Anaconda

Untuk mewujudkan semua lingkungan program yang relevan (perpustakaan ketergantungan, manajemen versi, dll.) yang diperlukan dalam artikel ini, cara termudah adalah menggunakan Anaconda.

Untuk metode instalasi Anaconda, silakan lihat panduan resmi Anaconda:https://www.anaconda.com/distribution/.

Artikel ini juga akan menggunakan numpy dan panda, dua perpustakaan populer dan penting dalam komputasi ilmiah Python.

Karya dasar di atas juga dapat merujuk pada artikel saya sebelumnya, yang memperkenalkan cara mengatur lingkungan Anaconda dan pustaka numpy dan panda.https://www.fmz.com/digest-topic/9863.

Kita menghasilkan target investasi acak dan faktor acak untuk memberi peringkat. mari kita asumsikan bahwa pengembalian masa depan kita benar-benar tergantung pada nilai faktor ini.

import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
## PROBLEM SETUP ##
# Generate stocks and a random factor value for them
stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)
# Generate future returns for these are dependent on our factor values
future_returns = current_factor_values + np.random.normal(0, 1, 10000)
# Put both the factor values and returns into one dataframe
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

Sekarang kita memiliki nilai faktor dan pengembalian, kita dapat melihat apa yang terjadi jika kita peringkat target investasi berdasarkan nilai faktor dan kemudian membuka posisi panjang dan pendek.

# Rank stocks
ranked_data = data.sort_values('Factor Value')
# Compute the returns of each basket with a basket size 500, so total (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)
for i in range(number_of_baskets):
    start = i * 500
    end = i * 500 + 500 
    basket_returns[i] = ranked_data[start:end]['Returns'].mean()
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

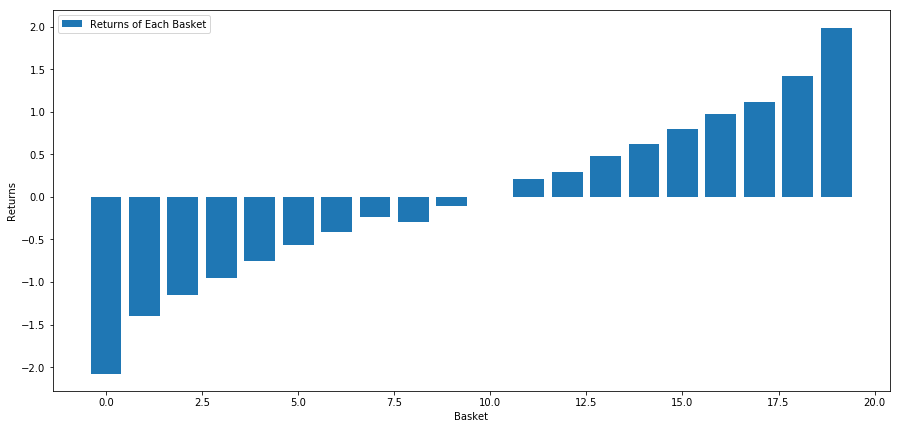
Strategi kami adalah untuk pergi panjang keranjang peringkat pertama dari investasi target kolam; pergi pendek dari keranjang peringkat kesepuluh.

basket_returns[number_of_baskets-1] - basket_returns[0]

Hasilnya adalah: 4.172

Menempatkan uang pada model peringkat kami sehingga dapat memisahkan target investasi berkinerja tinggi dari target investasi berkinerja rendah.

Keuntungan dari arbitrase berbasis peringkat adalah bahwa tidak dipengaruhi oleh gangguan pasar, sebaliknya gangguan pasar dapat digunakan.

Mari kita pertimbangkan contoh dunia nyata.

Kami memuat data untuk 32 saham di industri yang berbeda dalam indeks S&P 500 dan mencoba untuk memberi peringkat.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
                'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
                'HD','LOW','KO','LLY','MCD','MET','NEM',
                'PEP','PG','M','SWN','T','TGT',
                'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
price = 'adjClose'

Mari kita gunakan indikator momentum standar untuk periode waktu satu bulan sebagai dasar untuk peringkat.

## Define normalized momentum
def momentum(dataDf, period):
    return dataDf.sub(dataDf.shift(period), fill_value=0) / dataDf.iloc[-1]
## Load relevant prices in a dataframe
data = ds.getBookDataByFeature()['Adj Close']
#Let's load momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

Sekarang kita akan menganalisis perilaku saham kita dan melihat bagaimana saham kita beroperasi di pasar dalam faktor peringkat yang kita pilih.

Menganalisis data

Perilaku saham

Mari kita lihat bagaimana keranjang saham yang kita pilih berkinerja dalam model peringkat kita. Untuk melakukan ini, mari kita hitung pengembalian jangka panjang mingguan untuk semua saham. Kemudian kita dapat melihat korelasi antara pengembalian jangka panjang 1 minggu dari setiap saham dan momentum 30 hari sebelumnya. Saham yang menunjukkan korelasi positif adalah pengikut tren, sementara saham yang menunjukkan korelasi negatif adalah pembalikan rata-rata.

# Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = True)
# Calculate correlations between momentum and returns
correlations = pd.DataFrame(index = returns.columns, columns = ['Scores', 'pvalues'])
mscores = mscores[mscores.index.isin(returns.index)]
for i in correlations.index:
    score, pvalue = stats.spearmanr(mscores[i], returns[i])
    correlations[‘pvalues’].loc[i] = pvalue
    correlations[‘Scores’].loc[i] = score
correlations.dropna(inplace = True)
correlations.sort_values('Scores', inplace=True)
l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations['Scores'])
plt.xlabel('Stocks')
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.legend(['Correlation over All Data'])
plt.ylabel('Correlation between %s day Momentum Scores and %s-day forward returns by Stock'%(day,forward_return_day));
plt.show()

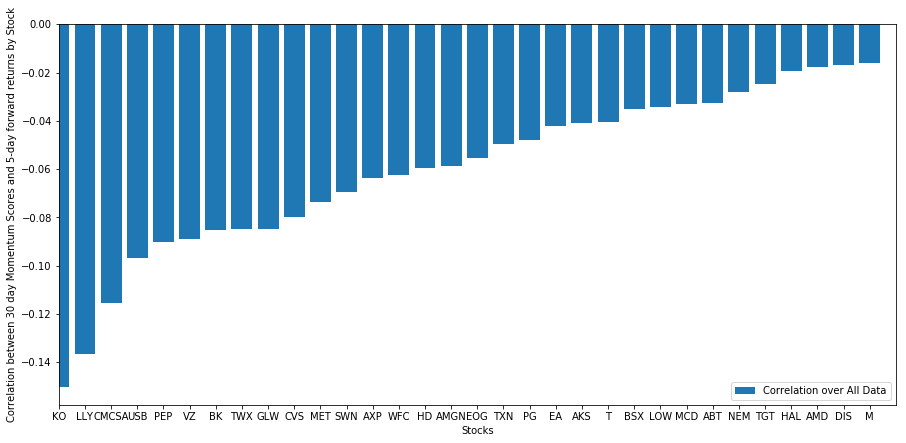
Semua saham kita memiliki reversi rata-rata sampai batas tertentu! (Tentu saja, alam semesta yang kita pilih bekerja seperti ini.) Ini memberi tahu kita bahwa jika saham berada di peringkat teratas dalam analisis momentum, kita harus mengharapkan mereka berkinerja buruk minggu depan.

Korélasi antara peringkat skor analisis momentum dan hasil

Selanjutnya, kita perlu melihat korelasi antara skor peringkat kita dan pengembalian jangka panjang keseluruhan pasar, yaitu hubungan antara tingkat pengembalian yang diprediksi dan faktor peringkat kita.

Untuk tujuan ini, kita menghitung korelasi harian antara momentum 30 hari dari semua saham dan pengembalian 1 minggu ke depan.

correl_scores = pd.DataFrame(index = returns.index.intersection(mscores.index), columns = ['Scores', 'pvalues'])
for i in correl_scores.index:
    score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
    correl_scores['pvalues'].loc[i] = pvalue
    correl_scores['Scores'].loc[i] = score
correl_scores.dropna(inplace = True)
l = correl_scores.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correl_scores['Scores'])
plt.hlines(np.mean(correl_scores['Scores']), 1,l+1, colors='r', linestyles='dashed')
plt.xlabel('Day')
plt.xlim((1, l+1))
plt.legend(['Mean Correlation over All Data', 'Daily Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

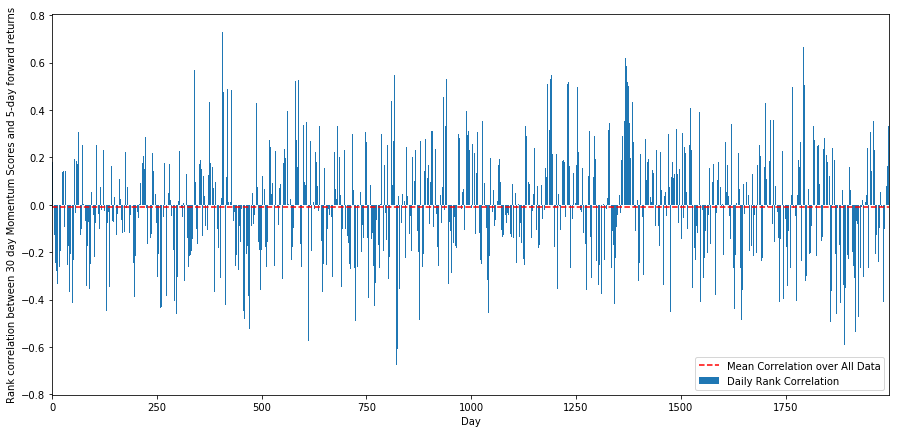
Korélasi harian menunjukkan korélasi yang sangat kompleks tetapi sangat kecil (yang diharapkan karena kita mengatakan semua saham akan kembali ke rata-rata).

monthly_mean_correl =correl_scores['Scores'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colors='r', linestyles='dashed')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

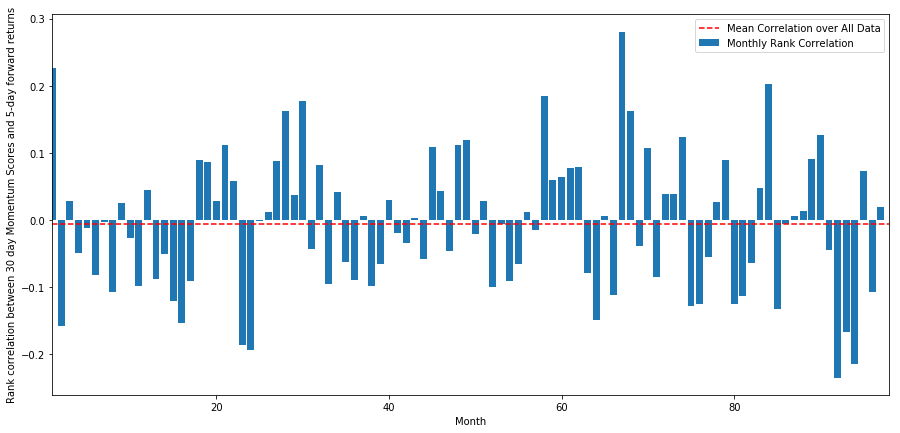
Kita dapat melihat bahwa korelasi rata-rata sedikit negatif lagi, tapi juga sangat berubah setiap bulan.

Rata-rata pengembalian pada keranjang saham

Kami telah menghitung pengembalian pada keranjang saham yang diambil dari peringkat kami. jika kita memberi peringkat semua saham dan membagi mereka ke dalam nn kelompok, apa rata-rata pengembalian dari setiap kelompok?

Langkah pertama adalah membuat fungsi yang akan memberikan rata-rata pengembalian dan faktor peringkat dari setiap keranjang yang diberikan setiap bulan.

def compute_basket_returns(factor, forward_returns, number_of_baskets, index):
data = pd.concat([factor.loc[index],forward_returns.loc[index]], axis=1)
    # Rank the equities on the factor values
    data.columns = ['Factor Value', 'Forward Returns']
    data.sort_values('Factor Value', inplace=True)
    # How many equities per basket
    equities_per_basket = np.floor(len(data.index) / number_of_baskets)
basket_returns = np.zeros(number_of_baskets)
# Compute the returns of each basket
    for i in range(number_of_baskets):
        start = i * equities_per_basket
        if i == number_of_baskets - 1:
            # Handle having a few extra in the last basket when our number of equities doesn't divide well
            end = len(data.index) - 1
        else:
            end = i * equities_per_basket + equities_per_basket
        # Actually compute the mean returns for each basket
        #s = data.index.iloc[start]
        #e = data.index.iloc[end]
        basket_returns[i] = data.iloc[int(start):int(end)]['Forward Returns'].mean()
        
    return basket_returns

Ketika kita memberi peringkat saham berdasarkan skor ini, kita menghitung rata-rata pengembalian setiap keranjang.

number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(float).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = True)
for m in forward_returns.index.intersection(resampled_scores.index):
    basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
    mean_basket_returns += basket_returns
mean_basket_returns /= l    
print(mean_basket_returns)
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

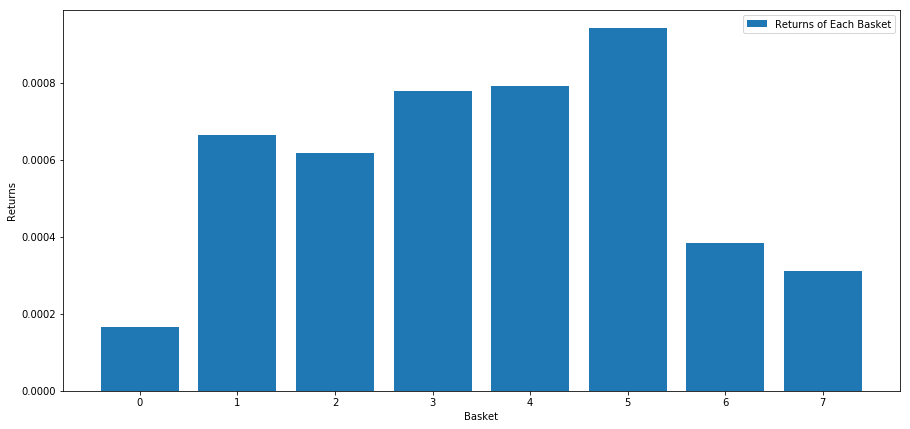
Tampaknya kita bisa memisahkan pelaku yang berkinerja tinggi dari pelaku yang berkinerja rendah.

Konsistensi margin (dasar)

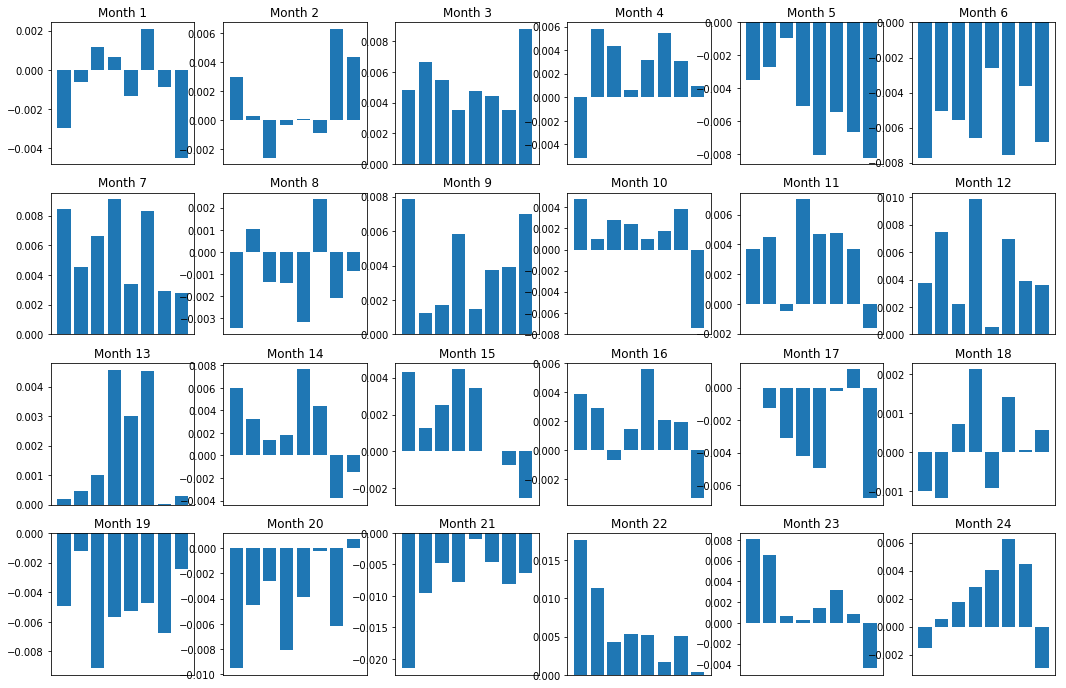
Tentu saja, ini hanya hubungan rata-rata. Untuk memahami seberapa konsisten hubungan itu dan apakah kita bersedia berdagang, kita harus mengubah pendekatan dan sikap kita terhadapnya dari waktu ke waktu. Selanjutnya, kita akan melihat margin bunga bulanan (basis) mereka untuk dua tahun sebelumnya.

total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
    temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[month]]
    temp_scores = resampled_scores.loc[monthly_index[month-1]:monthly_index[month]]
    for m in temp_returns.index.intersection(temp_scores.index):
        basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
        mean_basket_returns += basket_returns
    
    strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
    
    mean_basket_returns /= temp_returns.index.intersection(temp_scores.index).size
    
    r = int(np.floor((month-1) / 6))
    c = (month-1) % 6
    axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
    axarr[r, c].xaxis.set_visible(False)
    axarr[r, c].set_title('Month ' + str(month))
plt.show()

plt.figure(figsize=(15,7))
plt.plot(strategy_returns)
plt.ylabel('Returns')
plt.xlabel('Month')
plt.plot(strategy_returns.cumsum())
plt.legend(['Monthly Strategy Returns', 'Cumulative Strategy Returns'])
plt.show()

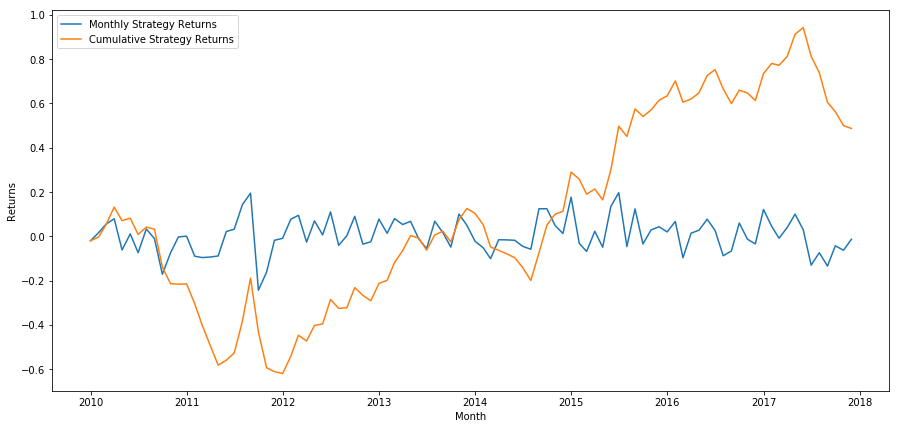
Akhirnya, jika kita pergi panjang keranjang terakhir dan pergi pendek keranjang pertama setiap bulan, maka mari kita lihat pengembalian (dengan asumsi alokasi modal yang sama per sekuritas).

total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

Tingkat pengembalian tahunan: 5,03%

Kita dapat melihat bahwa kita memiliki skema peringkat yang sangat lemah, yang hanya dapat membedakan saham berkinerja tinggi dari saham berkinerja rendah.

Temukan skema peringkat yang tepat

Untuk mewujudkan strategi ekuitas seimbang jangka pendek, sebenarnya, Anda hanya perlu menentukan skema peringkat. Semuanya setelah itu adalah mekanis. Setelah Anda memiliki strategi ekuitas seimbang jangka pendek, Anda dapat bertukar faktor peringkat yang berbeda tanpa banyak perubahan. Ini adalah cara yang sangat nyaman untuk mengulangi ide Anda dengan cepat tanpa khawatir tentang menyesuaikan semua kode setiap kali.

Skema peringkat juga dapat berasal dari hampir semua model. Ini tidak harus model faktor berbasis nilai. Ini bisa menjadi teknologi pembelajaran mesin yang dapat memprediksi pengembalian satu bulan sebelumnya dan peringkat sesuai dengan tingkat ini.

Pemilihan dan evaluasi sistem peringkat

Sistem peringkat adalah keuntungan dan bagian terpenting dari strategi ekuitas seimbang jangka pendek.

Titik awal yang baik adalah memilih teknologi yang sudah ada dan melihat apakah Anda dapat memodifikasinya sedikit untuk mendapatkan pengembalian yang lebih tinggi.

• Kloning dan penyesuaian: Pilih topik yang sering dibahas, dan lihat apakah Anda dapat memodifikasinya sedikit untuk mendapatkan keuntungan. Secara umum, faktor yang tersedia untuk umum tidak akan lagi memiliki sinyal perdagangan, karena mereka telah sepenuhnya melakukan arbitrase dari pasar.

• Model Pricing: Setiap model yang memprediksi pengembalian masa depan dapat menjadi faktor yang berpotensi dapat digunakan untuk memberi peringkat keranjang objek perdagangan Anda. Anda dapat mengambil model harga yang kompleks dan mengubahnya menjadi skema peringkat.

• Faktor berbasis harga (indikator teknis): faktor berbasis harga, seperti yang dibahas hari ini, memperoleh informasi tentang harga historis setiap ekuitas dan menggunakannya untuk menghasilkan nilai faktor. Contoh mungkin indikator rata-rata bergerak, indikator momentum, atau indikator volatilitas.

• Regresi dan momentum: Perlu dicatat bahwa beberapa faktor percaya bahwa setelah harga bergerak ke satu arah, mereka akan terus melakukannya, sementara beberapa faktor justru sebaliknya.

• Faktor dasar (berbasis nilai): Ini adalah kombinasi nilai dasar, seperti PE, dividen, dll. Nilai dasar berisi informasi yang berkaitan dengan fakta dunia nyata perusahaan, sehingga dapat lebih kuat daripada harga dalam banyak aspek.

Pada akhirnya, prediksi perkembangan adalah perlombaan persenjataan, dan Anda mencoba untuk tetap selangkah lebih maju. faktor akan arbitrase dari pasar dan memiliki umur yang berguna, sehingga Anda harus terus bekerja untuk menentukan berapa banyak resesi faktor Anda telah mengalami dan apa faktor baru dapat digunakan untuk menggantikannya.

Pertimbangan lain

• Frekuensi rebalancing

Setiap sistem peringkat memprediksi pengembalian dalam kerangka waktu yang sedikit berbeda. Regresi rata-rata berdasarkan harga mungkin dapat diprediksi dalam beberapa hari, sementara model faktor berdasarkan nilai mungkin dapat diprediksi dalam beberapa bulan. Penting untuk menentukan rentang waktu yang harus diprediksi model, dan melakukan verifikasi statistik sebelum melaksanakan strategi. Tentu saja, Anda tidak ingin overfit dengan mencoba mengoptimalkan frekuensi rebalancing. Anda pasti akan menemukan frekuensi acak yang lebih baik daripada frekuensi lain. Setelah Anda menentukan rentang waktu prediksi skema peringkat, cobalah untuk rebalancing pada frekuensi ini untuk memanfaatkan sepenuhnya model Anda.

• Kapasitas modal dan biaya transaksi

Setiap strategi memiliki volume modal minimum dan maksimum, dan ambang minimum biasanya ditentukan oleh biaya transaksi.

Perdagangan terlalu banyak saham akan menyebabkan biaya transaksi yang tinggi. Jika Anda ingin membeli 1.000 saham, itu akan dikenakan biaya ribuan dolar pada setiap rebalancing. Basis modal Anda harus cukup tinggi sehingga biaya transaksi dapat menyumbang sebagian kecil dari pengembalian yang dihasilkan strategi Anda. Misalnya, jika modal Anda adalah $ 100.000 dan strategi Anda menghasilkan 1% ($ 1.000) per bulan, semua pengembalian ini akan dikonsumsi oleh biaya transaksi. Anda perlu menjalankan strategi dengan jutaan dolar modal untuk mendapatkan lebih dari 1.000 saham.

Aset ambang batas terendah terutama tergantung pada jumlah saham yang diperdagangkan. Namun, kapasitas maksimum juga sangat tinggi. Strategi ekuitas seimbang jangka pendek dapat memperdagangkan ratusan juta dolar tanpa kehilangan keuntungan. Ini adalah fakta, karena strategi ini relatif jarang untuk rebalancing. Nilai dolar setiap saham akan sangat rendah ketika total aset dibagi dengan jumlah saham yang diperdagangkan. Anda tidak perlu khawatir tentang apakah volume perdagangan Anda akan mempengaruhi pasar. Misalkan Anda memperdagangkan 1.000 saham, yaitu 100.000.000 dolar. Jika Anda menyeimbangkan seluruh portofolio setiap bulan, setiap saham hanya akan diperdagangkan 100.000 saham per bulan, yang tidak cukup untuk menjadi pasar yang penting untuk sebagian besar sekuritas.

Berkaitan

Lebih banyak