リスクと利益の測定 - マルコウィッツ理論への紹介

先週 導入する際にポジションリスクの測定方法 - VaR 方法への紹介ポートフォリオのリスクは,個々の資産のリスクに等しくなく,その価格相関関係に関係している.例として2つの資産を挙げると,それらの相関関係が非常に強く,つまり一緒に上昇し落ちる場合,投資を多様化することでリスクは軽減されない.強い負の相関関係がある場合,多様化投資はリスクを大幅に削減することができる.自然に疑問が浮かび上がります.ポートフォリオに投資するときに一定のリスクで収益を最大化するにはどうすればいいですか?これは今日紹介するマルコウィッツ理論に導きます.

ハリー・マルコウィッツが1952年に提案した現代ポートフォリオ理論 (MPT) は,ポートフォリオ選択のための数学的枠組みである.リスクを制御しながらリスク資産の異なる組み合わせを選択することによって期待されるリターンを最大化することを目的としている.基本的な考えは,資産の価格が完全に互いに同期して動かないこと (すなわち,資産の間には不完全な相関性があること) で,投資リスク全体は多様化された資産配分によって軽減できる.

マルコウィッツ理論の鍵となる概念

1. 期待される収益率: 投資家が保有する資産や投資ポートフォリオから得ることを期待する収益で,通常は過去の収益データに基づいて予測されます.

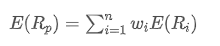
どこに?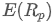ポートフォリオの期待される収益です.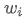ポートフォリオの i 番目の資産の重み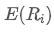i 番目の資産の期待される収益です.

2. リスク (波動性または標準偏差): 投資収益の不確実性や投資の変動を測定するために使用されます.

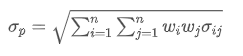
どこに?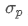ポートフォリオの総リスクを表します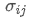資産iと資産jの共変数で,これらの2つの資産間の価格変化関係を測定します.

3. コヴァリアンス: 2つの資産の価格変化の相互関係を測定する.

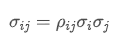
どこに?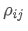資産iと資産jの相関係数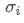そして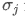資産iと資産jの標準偏差である.

4. 効率的な国境: リスク・リターン調整システムでは,効率の限界は,あるリスクレベルで最大期待できるリターンを提供できる投資ポートフォリオの集合です.

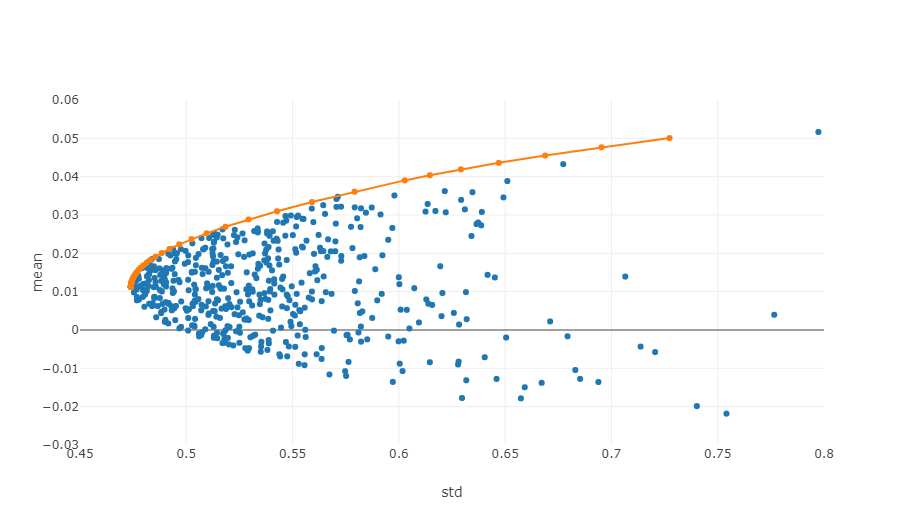
上記の図は,各点が異なる重量化された投資ポートフォリオを表す効率的な境界の例です.x軸はリスクレベルに等しい変動を示し,y軸はリターン率を表します.明らかに,私たちの焦点は,同じレベルのリスクで最も高いリターンを達成するため,グラフの上端にあります.

定量的な取引およびポートフォリオマネジメントでは,これらの原則を適用するには,歴史的なデータの統計分析と,さまざまな資産の期待されるリターン,標準偏差およびコヴァリアンスを推定するために数学的モデルを使用する必要があります.その後,最適化技術を使用して,最適な資産重量配分を見つけます.このプロセスには,しばしば複雑な数学的操作と広範なコンピュータ処理が含まれます.これが,現代金融で定量的な分析が非常に重要になった理由です.次に,特定のPython例で最適化する方法を示します.

シミュレーション方法を使用して最適な組み合わせを見つけるためのPythonコード例

Markowitz の最適なポートフォリオを計算することは,データ作成,ポートフォリオシミュレーション,指標計算などのいくつかの重要なステップを含む多段階のプロセスです.以下を参照してください:https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. 市場データを取得:

経由してget_data投資ポートフォリオを構築し,シャープ比率を計算するために使用されるリターンとリスクを計算するために必要なデータです.

2. 収益率とリスクを計算する:

についてcalculate_returns_riskこの関数は,各デジタル通貨の年収と年収リスク (標準偏差) を計算するために使用されました.これは,最適なポートフォリオで使用するために各資産の歴史的なパフォーマンスを定量化するために行われます.

3. マルコウィッツ最適ポートフォリオを計算する:

についてcalculate_optimal_portfolio複数の投資ポートフォリオをシミュレートするために使用された.各シミュレーションでは,資産の重みがランダムに生成され,これらの重みに基づいてポートフォリオの期待回報とリスクが計算された. 異なる重量を持つランダムな組み合わせを生成することで,最適な投資ポートフォリオを見つけるために複数の潜在的な投資ポートフォリオを調査することが可能である.これはマルコウィッツのポートフォリオ理論の核心的なアイデアの1つです.

このプロセスの目的は,あるリスクレベルで最も期待できるリターンを生み出す投資ポートフォリオを見つけることです.複数の可能な組み合わせをシミュレートすることで,投資家は異なる構成のパフォーマンスをよりよく理解し,投資目標とリスク耐性に最も適した組み合わせを選択することができます.この方法は投資決定を最適化し,投資をより効果的にすることができます.

import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# Obtain market data
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# Calculate Markowitz Optimal Portfolio
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # Convert weights to a list

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# Output results
print("Optimal combination:")
for i in range(len(symbols)):
    print(f"{symbols[i]} Weight: {optimal_weights[i]:.4f}")

print(f"Expected return rate: {optimal_return:.4f}")
print(f"Expected risk (standard deviation): {optimal_risk:.4f}")
print(f"Sharpe ratio: {optimal_return / optimal_risk:.4f}")

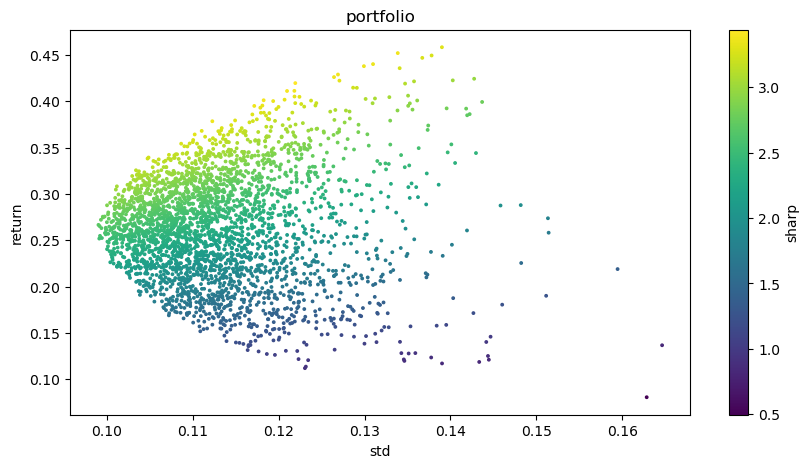
# Visualized investment portfolio
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

最終出力結果: 最適な組み合わせ: BTCUSDTの重み: 0.0721 ETHUSDTの重み: 0.2704 BNBUSDTの重み: 0.3646 LINKUSDTの重み: 0.1892 BCHUSDTの重み: 0.0829 LTCUSDTの重み: 0.0209 期待される収益率: 0.4195 予想されるリスク (標準偏差): 0.1219 シャープ比: 3.4403