プログラム化取引モデルを最適化する方法についてお話します
作者: リン・ハーン発明者 量化 - 微かな夢, 作成日: 2017-09-27 11:38:08, 更新日: 2017-09-27 11:39:08プログラム化取引モデルを最適化する方法についてお話します
- ### パラメータ高原とパラメータ島 ありがとうございました. パラメータ最適化における重要な原則は,パラメータ高原ではなくパラメータ孤島を目指すことである.パラメータ高原とは,パラメータ範囲がより広く存在し,このパラメータ範囲内ではモデルがよりよい結果を得ることを意味する.一般的に,高原の中心部でほぼ正規分布を形成する.パラメータ高原とは,パラメータ値が非常に小さな範囲内にある場合にのみモデルがよりうまく動作し,パラメータ値から逸脱するとモデルの表現が著しく変化することを意味する.
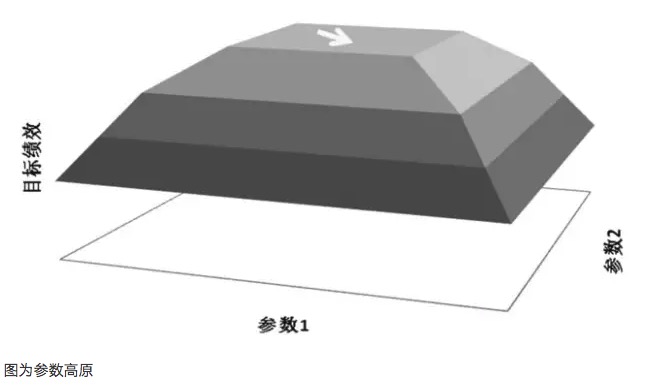
- #### グラフはパラメータ高原
参数高原示意図と参数孤島示意図を例に挙げると,ある取引モデルの内には,参数1と参数2の2つの参数があると仮定すると,両参数の横断テストを行った場合,3Dの業績図が得られる.良い参数分布は参数高原示意図であるべきであり,参数設定が偏差している場合でも,モデルの利益業績は保証される.このような参数が安定性があるため,モデルが将来の実戦であらゆる種類の取引に出会う場合,より強い反応性を有する.しかし,参数高原示意図のような参数横断後の業績の結果が,参数偏差が少ない場合,モデルの利益業績が大きく変化する場合は,このような参数性能が変化し,現実的な取引環境に対応することはしばしば困難である.
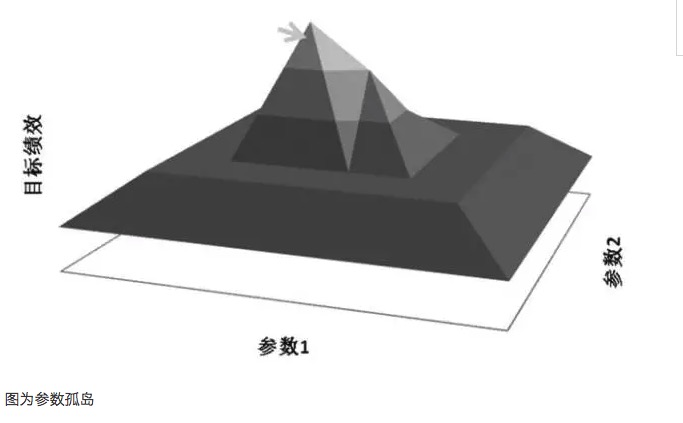
一般的に,近辺参数系が最適参数よりもはるかに差がある場合,この最適参数は過剰な和算の結果であり,数学的に探求する極大値ではなく奇点解であると考えられる可能性がある.数学的に見れば,奇点は不安定であり,将来の不確実な状況では,市場の特徴が変化すると,最適参数が最悪の参数になる可能性がある.
過剰適合は,選択されたサンプルの場合,選択されたサンプルが市場全体的な特徴を代表できない場合,テスト結果が正の期待値に達するためにのみパラメータを調整する行為である.この方法は,間違いなく自己欺瞞であり,パラメータ値が過剰適合の無効パラメータ値である.例えば,パラメータ過適合を分析することで,取引モデルは35と63の値で利回りが急増する現象が発生し,モデル内の対応指標が35と63のパラメータとして選択された場合,モデルの利回りは完璧に見えるが,実際には典型的なパラメータ孤島効果である.
過適合とパラメータ最適化の主な矛盾は,モデルパラメータ最適化の最適なパラメータは,既に行われた歴史的データサンプルのみに基づいていることであり,将来の市場はダイナミックな変化であり,歴史的な市場と比較して類似性も多様性も備わっています. モデルデザイナーは,モデルが歴史上最高のパフォーマンスを示すパラメータを見つけることができます. しかし,このパラメータは将来のモデルの実用アプリケーションで必ずしも最高のパフォーマンスを発揮する必要はありません.
さらに,パラメータ高原とパラメータ孤島は,取引回数にもより大きな関係がある. モデルが取引回数が少ない場合,モデルがこれらの取引回数で利益を得るのに適切なパラメータポイントがしばしば見つけられる. このパラメータ最適化されたモデルは,利益がより偶然であることを表現する. モデルが取引回数が多くなった場合,モデルの利益の偶然性は低下し,利益の必然性と規則性をより表現するパラメータ高原が存在します. このパラメータ最適化モデルはパラメータ最適化の目的のために行われます.
- ### パラメータを最適化する方法
参数平原と参数孤島を理解した後に,参数最適化の方法が重要であることが明らかになった.特に,モデルに複数の参数 (以下参数群) が存在する場合,しばしば1つの参数の取値が他の参数平原の分布に影響を与える.では,参数群をどのように最適化するか.
ある方法は,段階的な収束法である.つまり,まず1つのパラメータを個別に最適化し,その最適値を得て固定し,次に別のパラメータを最適化し,その最適値を得て固定する.このように循環して,最適化結果は変化しない.例えば,均線交差取引モデルでは,二つの独立したパラメータが均線短周期N1と周期長周期N2である.まずN2を1に固定し,N1を1〜100の数値範囲でテストフィルタで選んで,最適なパラメータを探し,最終的に最適なパラメータを8に固定し;その後,N2を1200から最適値26に最適化し,最終的に最適値26を得て固定する.また,N1を2回目最適化し,新しい最適値10を得て固定する;最後にN2を最適化し,最終的に最適値28を固定する.このように循環して,最適化の結果を選んで,最終的に停止するまで最適化する.N2の最適値N1〜10,30の最適値が,このパラメータのために動作する.
別の方法は,より強力な計算機能を持つプログラムソフトウェア設計プラットフォームを利用して,目標関数と参数列の間の分布を直接計算し,その後多次元差分の分布を求め,差分の絶対値が
パラメータ最適化方法に加えて,データサンプル選択も重要な要因である.トレンドを追跡するモデルがトレンド市場が出現するときにうまく機能し,高売り低買いする戦略が波動市場でうまく機能する.したがって,パラメータ最適化では,利益を考慮するために一致する市場を適切に排除し,損失を考慮するために,キスしない戦略思想の市場データを追加する必要があります.
株式指数先物として,上場初期2010年と,急激な牛市が発生した2014年下半期から現在まで,株式指数先物は片方市場である.疑いなく,すべてのトレンドモデルが良い結果をもたらす.しかし,この急激な市場データをサンプルに追加してパラメータ最適化を行なった場合,モデルパラメータは必ずしも最適ではない.
例えば,あるモデルに2つのパラメータがあると仮定すると,パラメータAのテスト結果は,片側市場時間帯で非常に良く,他の時間帯では一般的に表現される.別のパラメータBのテスト結果は,片側市場時間帯でパラメータAよりも劣り,他の時間帯ではパラメータAよりも優れている.各時間帯間の分布は比較してパラメータAが均等である.たとえパラメータAが,サンプルデータ全体のテストの総合指標であるリスク・リターンなどの比率がBパラメータよりも高い場合でも,パラメータBは比較的に安定しているため,特定のサンプルに依存していないため,パラメータBを選ぶ傾向がある.
要するに,程序化された取引モデルを構築する際には,一方,モデルをパラメータ最適化によって改良し,価格変動のモデルにより適性を与え,投資収益性を向上させることができる.一方,パラメータ最適化に対する過度に適合を防止し,市場の変化に対するモデルの適用性を大幅に低下させる.
プログラミングトレーダーから転送
- 金のフォークの死線はどのように作られるか?
- 内蔵関数_Cross 解析と使用説明
- プランが切れたのに 私はプランを買ったことがない
- 分散型取引所からデータを入手するにはどうすればいいですか?
- デジタル通貨の格差モニタリング分析 実体分析 BitcoinとBitfinexがうまく機能していない
- Poloniex はエラー? (Exchange_Register): platformId: 27, currency: BTC_ETC, Msg: Peroid not support Register FILE:803 reg FILE:1264 コメントを表示する
- 特定の取引所のシリアル番号は?
- 投資を量的に見てみましょう
- 返信では,
の収益曲線は の手数料を算出していないか? - 虫を捕まえて,収益を予測する質問に誤った語句が書かれています
- 発明者による定量化図で,横軸の座標は時間軸ではなく,数字の柱形図や折りたたみ図を描く方法について教えて下さい.
- メディアの報道によると,OKEXの問題は,
- 海外の知名取引所の利弊と開設ガイド
- 取引量に関するいくつかの誤解を明らかにする
- 市場技術分析グラフに時間がないか?
- 機械学習について知っておくべき10の真実
- 発明者数量化に似たコミュニティは 他国でもありますか?
- ビットコインは,結局のところ,権力ゲームです
- GetPosition () が返した Position のProfit の説明を教えて下さい.
- モントカーロ・シミュレーションは 未来を予測する方法を 知りたかったら