数学とギャンブル

• 賭博は確率のゲームであり,数学者のパスカルと大数学者のフェルマの興味を引いたのは,奇妙な賭博の結果であり,彼らは手紙を通じて,確率論の原理を提案し,その結果,確率論を創設した.今日の数は,賭博のいくつかの確率の趣味を紹介する.賭博をするには,細かい計算をしなければなりません.

• 1. 完璧なギャンブル

NBAのチームである湖人チームと小牛チームの試合があり,両チームとも忠実なファンがいて,彼らを人族と牛族と呼んでください。ファンはもちろん,自分の支持するチームが勝つ可能性が高いと感じているので,あなたに賭けたいと思います。人族が湖人の勝つ確率がpであると仮定し,牛族が小牛の勝つ確率がq,pとqであると仮定すると,どちらも50%以上でなければならない。次に面白い部分があります.私たちは常に簡単に,人族と牛族と賭ける方法を設計することができますが,結果がどうであれ,私たちは賭けても負けることがありません!

方法としては,族と牛族と同じく, y 元を勝ち,x 元を負けると, y>x であれば,になります. そして,x と y は,以下の2つの簡単な不等式を満たすだけで,族と牛族の期待利益が正になるので,

```
p * x - ( 1-p ) * y > 0
q * x - ( 1-q ) * y > 0
```

y>xの制限を加えると,描かれた図は3つの直線で囲まれた領域であり,その中の任意の点の座標値 ((x,y) は必勝方案である.p>qであれば,解は以下の図の青い部分である.

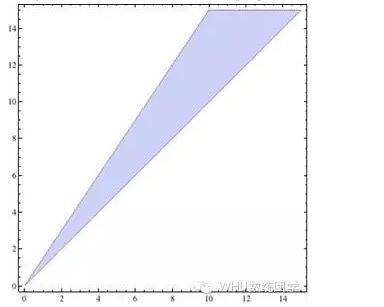
この問題は完璧に解決されたように見えるが,もう一つ疑問は,読者がすぐにその馬鹿げたところを見いだすだろう:族のと牛族のは,彼らの期待収益は正しかった,つまり,長期的には,彼らはお金を得ているが,私たちは安定して儲けています.

• ### カード2と3の詐欺

これは別の巧妙なパズルで,まず3枚のカードを用意します. 1番のカードは正反対は黒で,2番のカードは正反対は赤で,3番のカードは片側が黒で,片側が赤です. そして,カードを箱に入れ,振って,相手が平面を抽出してテーブルに置きます. そして,対面の色のパズルは正面と同じです. このパズルは公平に見えます. 例えば,表面に黒のカードを抽出すると,カードは1番か3番か,対面の色のパズルは黒か赤か,直感的にはそれぞれが1/2の確率になります.

勝った確率は1/2ではなく2/3です. このゲームで最も困惑するのは,カードの2面性です. プレイヤーは3面ではなく6面 (3黒面,3赤面) を引きます. この6面をA,B,C,D,E,Fと番号で表します.

プレイヤーは黒面に抽出すると,A,C,D の3つの可能性があり,その背面はそれぞれD,F,Aで,黒のケースは2/3を占める.

この問題は1889年にフランスの数学者ベルトランによって最初に提唱され,結果が予想外であったため,ベルトランの箱パラドックスとも呼ばれ, 1950年にアメリカの数学者ウォレン・ウィーバーが上記のカードゲームを紹介し,マーティン・ガードナーはこれを”三枚のカードの詐欺”と呼んだ.

• ### 3 奇妙なナマケモノA

時々,私たちは賭博を始める前に,水を流し,他の人に小さなお金を稼ぐようにし,長線を投げて大きな魚を捕まえて,最後に一つの網を投げます. 以下は素晴らしい例です. 四人がブリッジカードをプレイしているとき,私はまずこう言います. “さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ,さあ”.

この2つのの違いを考える人は多いでしょうが,その違いは信じられないほど大きいのです. まず,最初のの確率を考えてみましょう.

  没有A的情形：C（48，13）
  至少有1张A的情形：C（52，13）－C（48，13）
  恰好有1张A的情形：4＊C（48，12）
  至少有2张A的情形：C（52，13）－C（48，13）－4＊C（48，12）
  事件X为至少有两张A，事件Y为至少有一张A，那么条件概率为：

  P（X｜Y）＝P（XY）／P（Y）=(C（52，13）－C（48，13）－4＊C（48，12）)/(C（52，13）－C（48，13）)≈37%

この時,私は自分自身にAを賭け,負けやすいだろう.しかし,最初のの敷設の後,みんなの賭けの意向は動員されました.二番目のは,服を着替えているだけではありませんか,と,彼らは大きな賭けをしました.そして,私はより多くのAを持っていない,そして,中途半端に私たちの下にある.以下では,第二のの確率は大きく異なっていることを発見します.

  有黑桃A的情形：C（51，12）
  没有其它A的情形：C（48，12）
  还有其它A的情形：C（51，12）－C（48，12）
  事件X为还有其它A，事件Y为有黑桃A，条件概率为：

  P（X｜Y）＝P（XY）／P（Y）＝（C（51，12）－C（48，12））／C（51，12）≈56%。

WHUの数学グループ学