LSTMフレームワークを使ってビットコインの価格をリアルタイムで予測する

このケースは,学習研究目的のみであり,投資提案ではありません.

ビットコインの価格データは時間軸に基づいているため,ビットコインの価格予測は主にLSTMモデルを用いて行われます.

長期短期記憶 (LSTM) は,特に時間序列データ (または映画,文言などの時間/空間/構造順序を持つデータ) に適用される深層学習モデルであり,仮想通貨の価格走行を予測する理想的なモデルである.

この記事では,LSTMによるデータの組み合わせにより,ビットコインの将来の価格を予測する.

データベースをインポートする

import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

データ分析

データをアップロード

"BTCの日々の取引データを読む"

data = pd.read_csv(filepath_or_buffer="btc_data_day")

データの表示は,現在1380件のデータがあり,データ列はDate、Open、High、Low、Close、Volume (BTC),Volume (Currency) ・Weighted Priceで構成されています. Date列を除いて,他のすべてのデータ列はfloat64データタイプです.

data.info()

この10行目のデータを見てください

data.head(10)

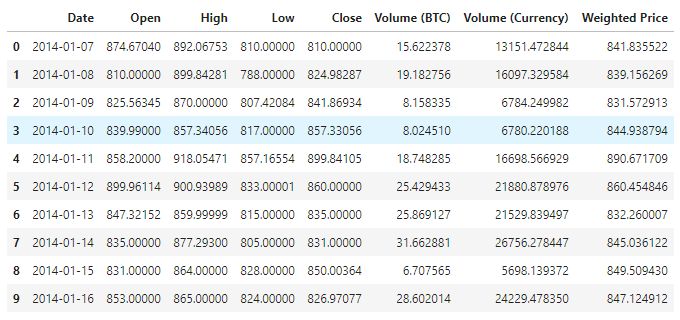
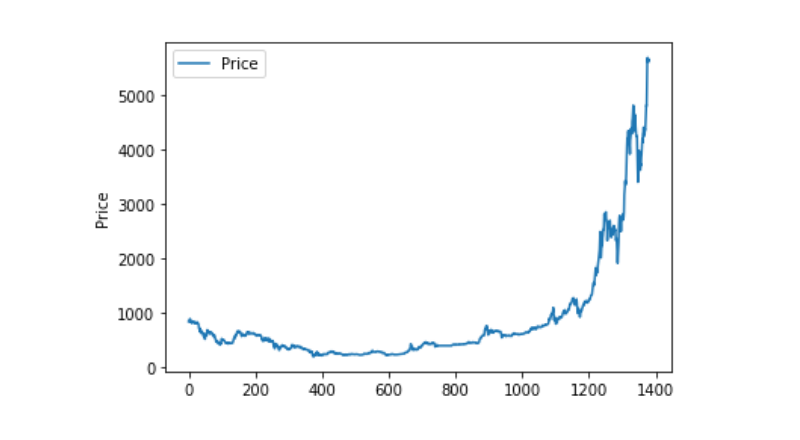
データの可視化

matplotlib で,データ分布と動向を観察するために,Weighted Price を描く.図では,データ 0 の部分を見つけ,異常がないかどうかを確認する必要があります.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

異常データ処理

このデータにナンのデータが含まれているか確認します.

data.isnull().sum()

Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

この0のデータを見てみましょう. この0のデータには0があります.

(data == 0).astype(int).any()

Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

(data == 0).astype(int).any()

Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

曲線が非常に連続しているので,この曲線は,この曲線が,この曲線が,この曲線が,この曲線が,この曲線が,この曲線が,この曲線が,この曲線が

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

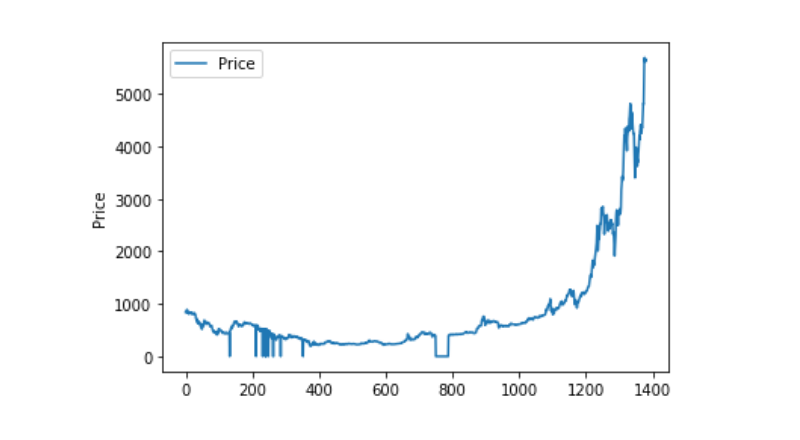
トレーニングデータセットとテストデータセットの分割

データを0−1にまとめます

data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

テストデータセットとトレーニングデータセットを2-8で分割します.

ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

訓練データセットとテストデータセットを作成します. 訓練データセットとテストデータセットを1日間のウィンドウで作成します.

def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

モデルを定義し訓練する

このとき,簡単なモデルを使います. そのモデル構造は1. LSTM2. Dense.

この LSTM の入力形について説明する必要があります. Input Shape の入力次元は ((batch_size, time steps, features) です. ここで,time steps の値はデータ入力時のタイムウィンドウ間隔であり,ここで私たちは1日をタイムウィンドウとして使用しており,私たちのデータは日データなので,ここで私たちのタイムステップは1です.

長期短期記憶 (Long short-term memory, LSTM) は,長連続訓練における梯度失踪と梯度爆発の問題を解決するために主に用いられる特殊なRNNである.

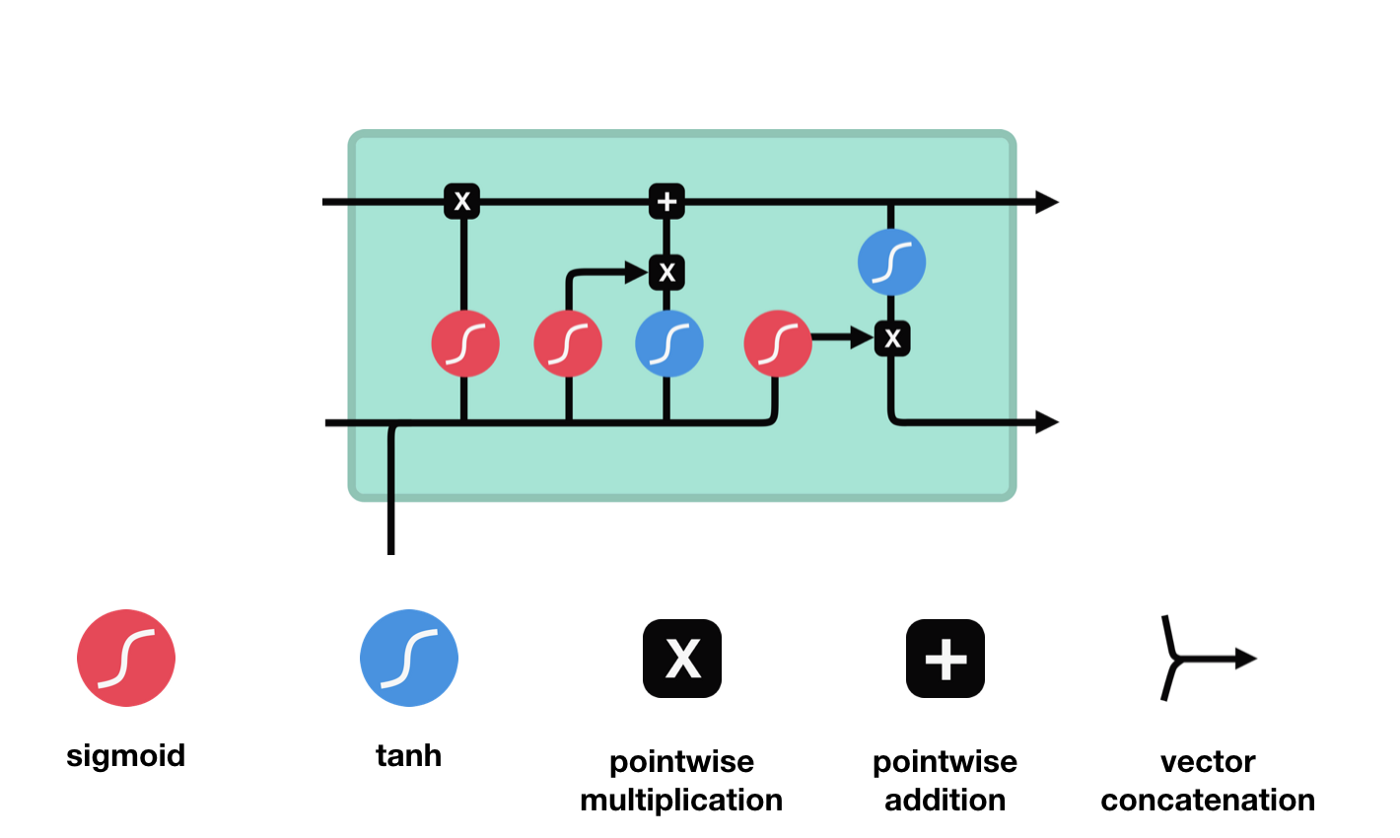
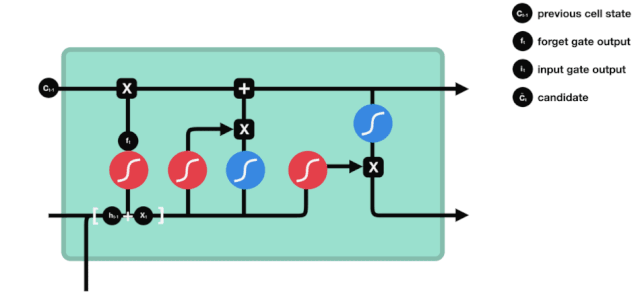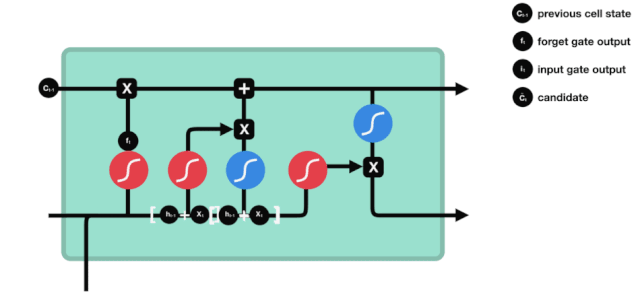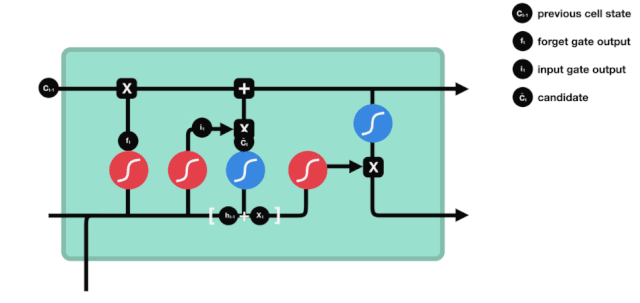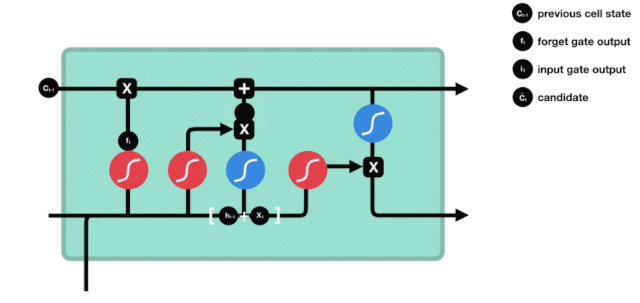
LSTMのネットワーク構造図から,LSTMは実際には小さなモデルであり,3つのシグモイド活性化関数,2つのタンハ活性化関数,3つの乘法,1つの加算関数を含むことがわかります.

細胞の状態

細胞の状態はLSTMの中心であり,上図の最上部にある黒い線であり,この黒い線の下にはいくつかの扉があります. 細胞の状態は,それぞれの扉の結果に基づいて更新されます.

LSTMネットワークは,ゲートと呼ばれる構造によって細胞の状態に関する情報を削除または追加する.ゲートは,どの情報が通過するかを選択的に決定することができる.ゲートの構造は,シグモイド層と点掛け操作の組み合わせである.シグモイド層の出力は0−1であり,0は通過できないことを表す.そして1は通過することを表す.LSTMには3つのゲートが含まれ,細胞の状態を制御する.以下では,これらのゲートを1つずつ説明します.

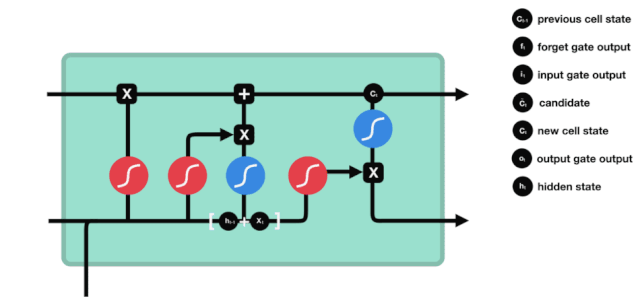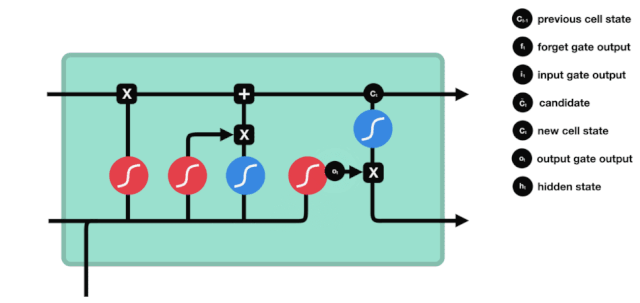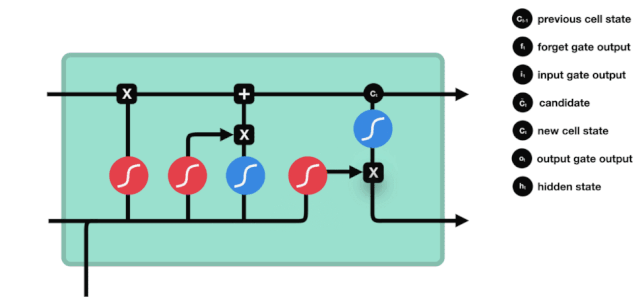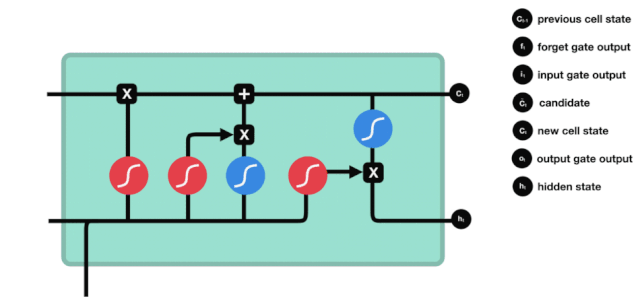
忘れられた扉

LSTMの最初のステップは,細胞の状態がどの情報を捨てるべきかを決定することである.この部分操作は,忘却門と呼ばれるシグモイドユニットによって処理される.

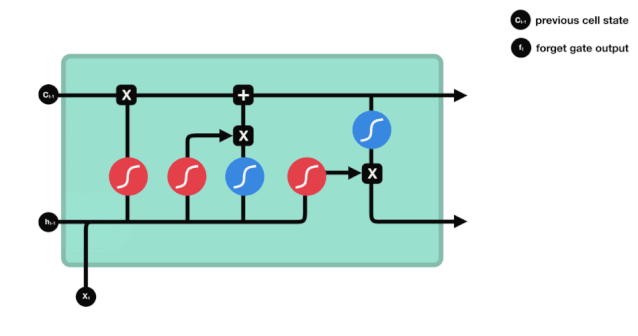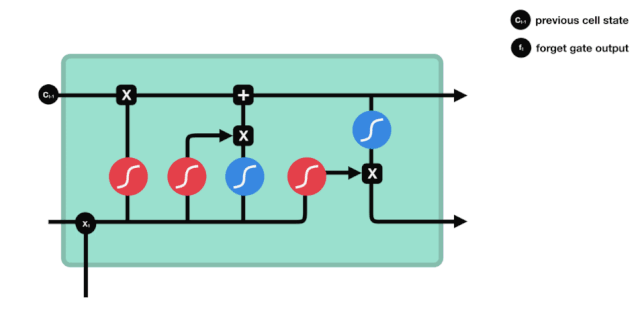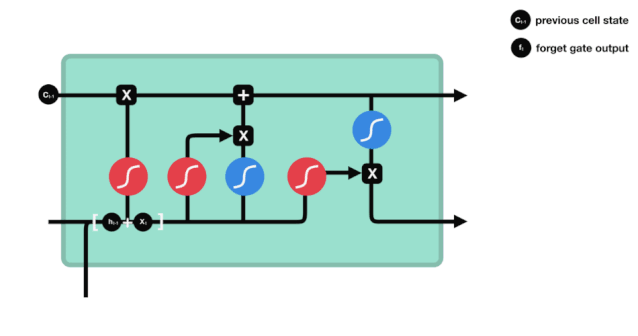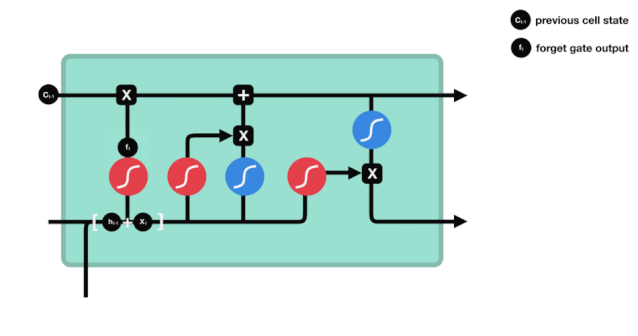
忘却門は,$h_{l-1}$と$x_{t}$の情報を参照して,0-1のベクトルを出力し,そのベクトルの0−1値は,細胞状態$C_{t-1}$のどれだけの情報が保持されているかまたは廃棄されているかを示しています.0は保持されていないことを示し,1は保持されていることを示します.

数学表現: $f_{t}=\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right) $

入り口

次のステップは,細胞状態に新しい情報を追加する決定です. このステップは入力ドアを開けることで完了します.

$h_{l-1}$と $x_{t}$の情報は,また,忘却門 (sigmoid) と入力門 (tanh) に入れられている.忘却門の出力は0-1の値であるため,忘却門の出力は0である場合,入力後の結果$C_{i}$は,現在の細胞状態に追加されないし,1である場合,全部細胞状態に追加される.したがって,忘却門の役割は,入力門の結果を選択的に細胞状態に追加することです.

公式は $C_{t}=f_{t} * C_{t-1}+i_{t} * \tilde{C}_{t}$

出口ドア

細胞の状態を更新した後に$h_{l-1}$と$x_{t}$の合計によって入力された状態の特徴に基づいて出力細胞のどの状態特性を判断する必要がある.ここで,入力されたものは出力門と呼ばれるsigmoid層を通過して判断条件を得,それから細胞の状態をtanh層を通過して -1〜1の間の値を得るベクトルを得ます.このベクトルは出力門からの判断条件に掛けられ,最終的にこのRNNユニットの出力を得ます.

def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

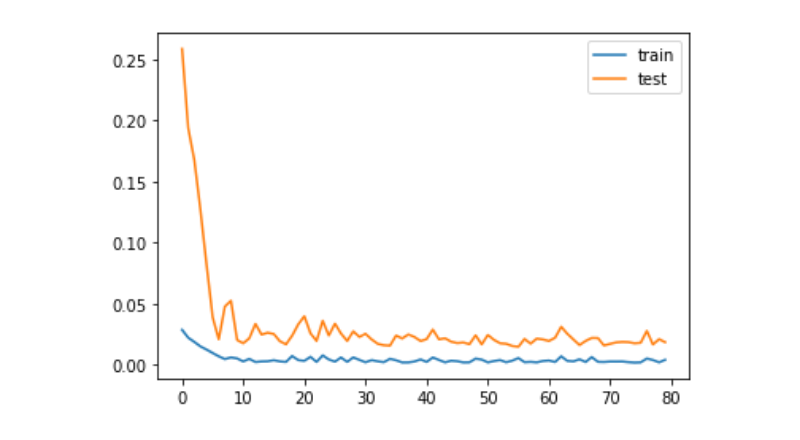
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

予測

predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

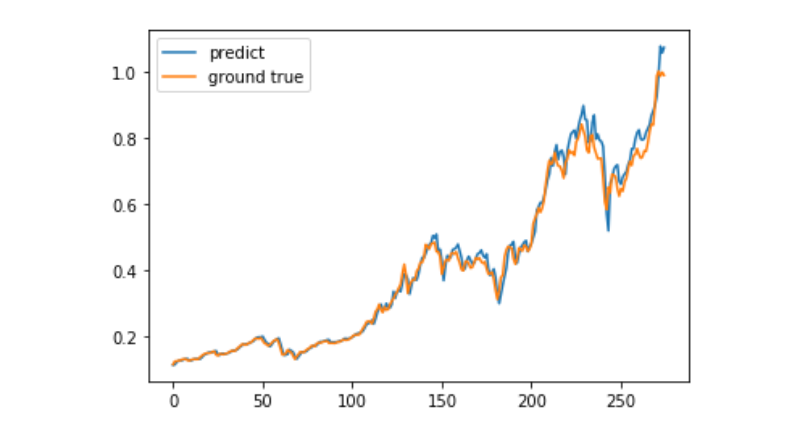
現在,機械学習を用いてビットコインの長期的価格動向を予測することは非常に困難であり,この記事は学習事例としてのみ使用できる.このケースは,その後,Matrix Pool Cloudのデモ画像の中でオンラインになり,興味のあるユーザーが直接体験することができます.

もっと