隠れマルコフモデル

• ### “認識する”

HMMは,株価に直接適用されるので,このHMMは,株価に直接適用されるので,このHMMは,株価に直接適用されるので,このHMMは,株価に直接適用されるので,このHMMは,株価に直接適用されるので,このHMMは,株価に直接適用されます.

マルコフ・チェーンとは,まずは,高級な音がするものの,その意味が全くわからないものですが,まずはマルコフ・チェーンについて見てみましょう.

マルコフ連鎖は,アンドレ・マルコフ (A.A. Markov,1856-1922) にちなんで名付けられている.これは,数学においてマルコフ性質の離散事件のランダムな過程を指す.現在の知識や情報を与えられた場合,過去 (すなわち現在以前の歴史的状態) は,未来 (すなわち現在後の将来の状態) を予測するのに無関係である.

この過程において,各状態の移転は先のnつの状態のみに依存し,この過程は1つのn級のモデルと呼ばれ,nは移転状態に影響する数のことです.最も単純なマルコフ過程は,各状態の移転が先の1つの状態のみに依存する一級のプロセスです.

• ### 2つ目の例は

グラフの表記は以下の通りです.

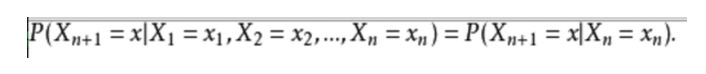
日常の例を挙げると,現在の天気状況に基づいて将来の天気状況を予測したいと思います.一つの方法は,このモデルの各状態が前者の状態のみに依存していると仮定することです.マルコフ仮説,この仮説は,この問題を非常に簡素化します.もちろん,この例は,ある程度非現実的です.しかし,このような簡素化されたシステムは,私たちの分析に有利であるため,私たちは通常,このような仮説を受け入れます.なぜなら,このようなシステムは,非常に正確ではないが,いくつかの有用な情報を得ることを可能にするからです.

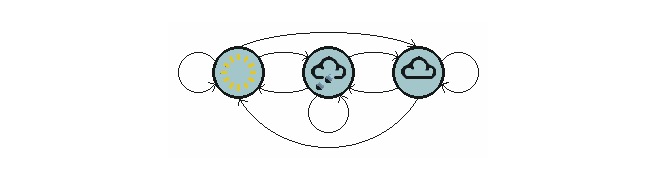
上の図は,天候が移動するモデルを示しています.

Nつの状態を含む一段階のプロセスにはN2つの状態移転があることに注意してください. それぞれの移転の確率は,状態移転の確率と呼ばれ,つまり,一つの状態から別の状態への移転の確率です. これらのN2の確率はすべて,状態移転マトリックスを用いて表現できます.上記の天気例の状態移転マトリックスは次のとおりです.

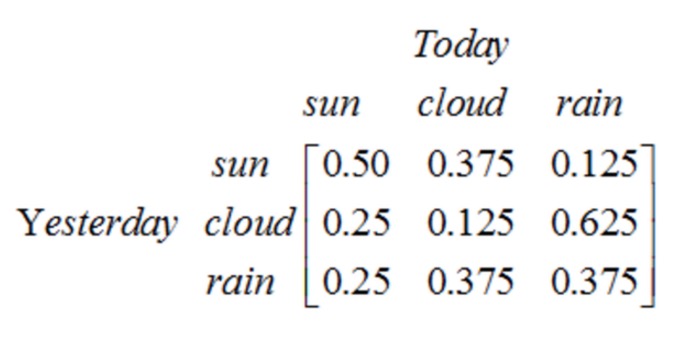
この行列は,もし昨日曇っていたら,今日晴れる確率は25%,曇る確率は12.5%,雨が降る確率は62.5%であると示しています. 明らかに,この行列の各行の合計は1。

確率ベクトルの初期化には,

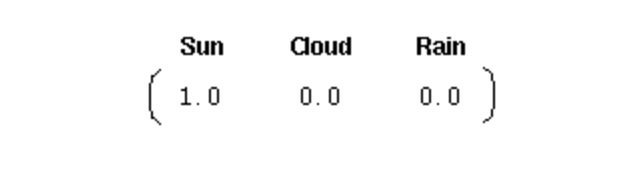
このベクトルは,1日目は晴れた日であることを示している.ここでは,上記の1次マルコフプロセスには以下の3つの部分が定義されている.

晴れ,曇り,雨が降る

初期ベクトル:時間0時にシステムの状態を定義する確率.

状態移転マトリックス:各気象変換の確率。このように記述できるすべてのシステムはマルコフ過程。

しかし,マルコフプロセスは十分には強力でない場合,どうすればよいでしょうか?

例えば,私たちの株式市場では,単に市場を観察するだけで,当日の価格,取引量などの情報しか知り得ないが,現在の株式市場の状態がどのようなものかわからない ((牛市,熊市,震動,反弹など),この場合,私たちは2つの状態の集合,観察可能な状態の集合 ((株式市場の価格取引量状態など) と隠された状態の集合 ((株式市場の状況)) を持っている.我々は,株式市場の価格取引量状態とマルコフ仮説に基づいて株式市場の状況を予測できるアルゴリズムを見つけることを望んでいます.

上記の例では,観察可能な状態の連続と隠された状態の連続は確率に関連している.したがって,このタイプのプロセスを,隠されたマルコフプロセスと,この隠されたマルコフプロセスの確率に関連して観察可能な状態の集合である隠されたマルコフモデルとしてモデル化することができる.

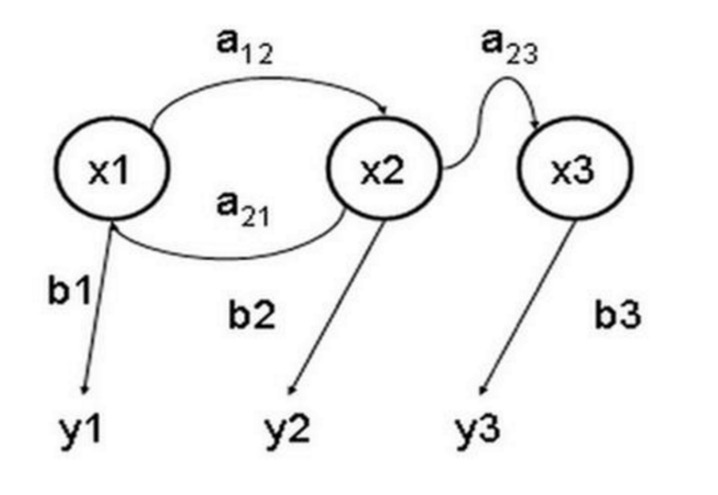
隠されたマルコフ模型 (Hidden Markov Model) は,隠された未知パラメータを含むマルコフプロセスを記述するための統計モデルである.その難しさは,観察可能なパラメータからそのプロセスの隠されたパラメータを特定し,そのパラメータを使用してさらなる分析を行うことである.下図は,3つの状態の隠されたマルコフモデル状態移転図であり,xは隠された状態を表し,yは観察可能な出力を表し,aは状態移転確率を表し,bは出力確率を表している.

の例で説明しましょう.私が手中に3つの異なるを持っていると仮定しましょう.最初のは,私たちが普段使うである (このをD6と呼びましょう),6つの面があり,それぞれの面 (1,2,3,4,5,6) が出現する確率は1/6です.第二のは,四面体である (このをD4と呼びましょう),それぞれの面 (1,(2,3,4) が出現する確率は1/4です.第三のには8つの面 (このをD8と呼びましょう),それぞれの面 (このをD8と呼びましょう) が出現する確率は1/8です.

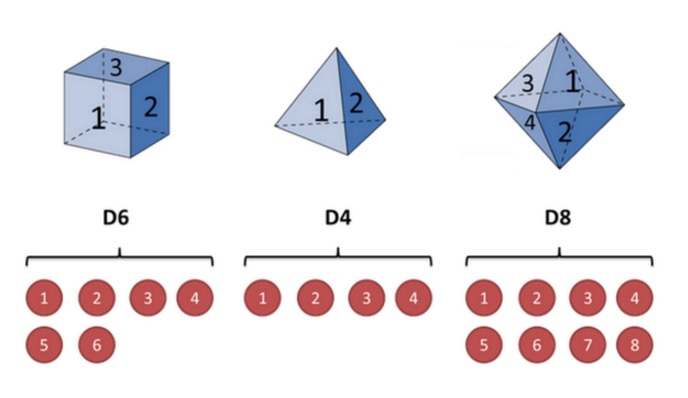
3つのから1つを選びます. 確率は1/3です. そして,1,2,3,4,5,6,7,8の1つの数字を選びます. 繰り返し繰り返すと,数字の列が出来て,数字はそれぞれ1,2,3,4,5,6,7,8の1つになります.

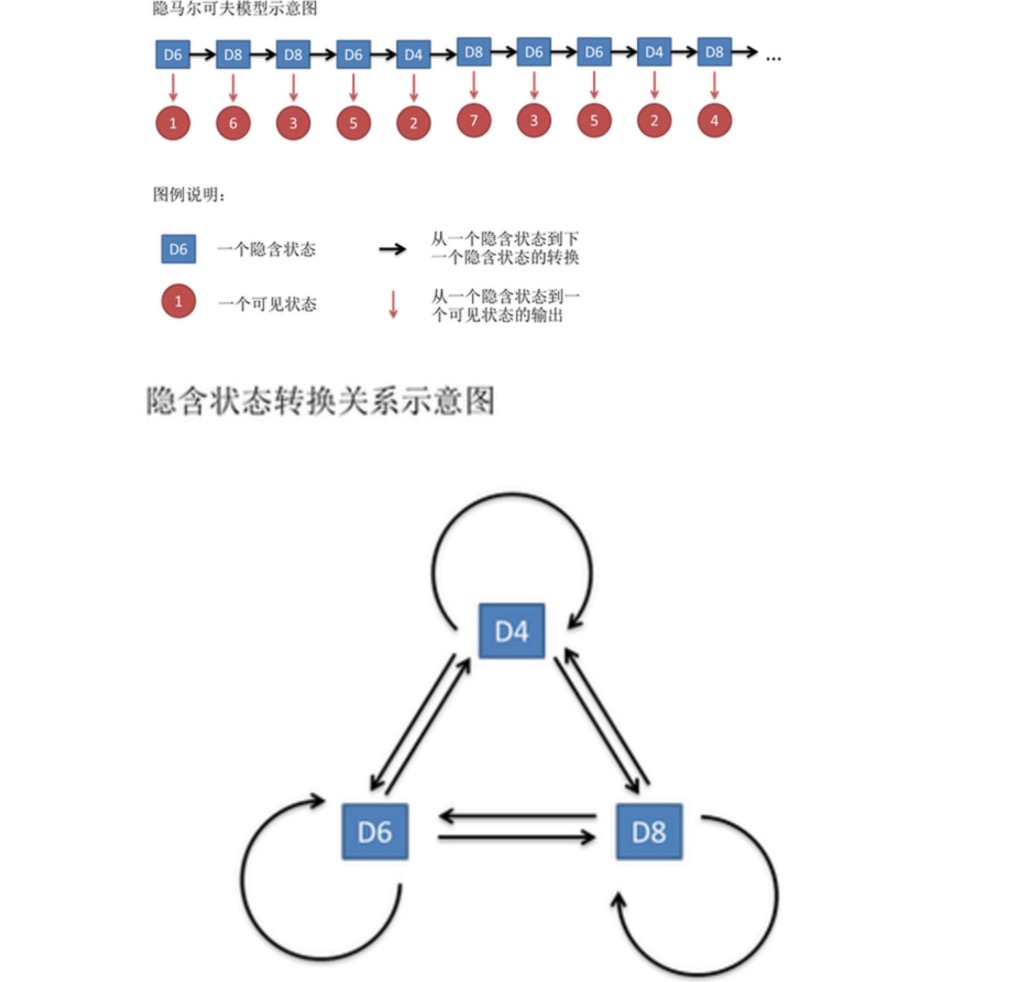
この数列は,可視状態の連鎖と呼ばれています. しかし,暗黒マルコフモデルでは,このような可視状態の連鎖だけでなく,暗黒状態の連鎖もあります. この例では,暗黒状態の連鎖は,あなたが使っているの序列です. 例えば,暗黒状態の連鎖は,D4 D6 D8 D6 D4 D8 D6 D6 D4 かもしれません.

一般的に,HMMで言うマルコフ連鎖は,実際には隠された状態の連鎖を指す,隠された状態 () の間に変換の確率があるからである.この例では,D6の次の状態はD4,D6,D8の確率は1/3である。D4,D8の次の状態はD4,D6,D8の変換の確率も1/3である。このように設定するのは,最初に簡単に言うために,しかし,実際には,変換の確率を任意に設定することができる。例えば,D6の後にD4が接着しない,D6の後にD6の確率は0.9,D8の確率は0.1である。このような新しいHMMである。

同様に,目に見える状態の間の変換確率はなくとも,隠された状態と目に見える状態の間の確率は出力確率と呼ばれます.私たちの例では,六面 ((D6) が1を生成する出力確率は1/6です. 2,3,4,5,6を生成する出力確率も1/6です.また,出力確率の別の定義もできます.例えば,私が賭場で手足を動かされた六面を持っているので,出力する確率は1より大きく,¹⁄₂,出力する確率は2,3,4,5,6で1/10です.

実際,HMMの場合,すべての隠された状態の間の変換確率と,すべての隠された状態からすべての可視状態の間の出力確率を事前に知っていたら,シミュレーションを行うことはかなり簡単である.しかし,HMMモデルを適用すると,多くの場合,一部の情報が欠けている.時には,が何種類あるか,各種のが何であるかを知っていても,が出たのシーケンスがわからない.時には,多くのの結果を何度も見ただけで,残りのことは何も知らない.もし,これらの欠けている情報を推定するアルゴリズムを適用すると,非常に重要な問題になる.

HMMモデルに関連するアルゴリズムは主に3つのカテゴリーに分けられ,それぞれ3つの問題を解く.

• が何種類あるか ((隠された状態の数),各種のが何種類あるか ((変換確率),の出結果によって ((可視状態の鎖),毎回出されるのはどの種類のか ((隠された状態の鎖) を知りたい。

• また,のいくつがあるか, (隠された状態の数),それぞれのが何であるか, (変換確率),から得られた結果によって (可視状態の鎖),この結果を得る確率を知りたい。

• の種類がいくつあるかを知って ((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((

  株式市場の問題を解くには,問題1と問題3を解決する必要があります. 次の記事では,その方法について説明します.

投稿者:Moneycode コラムより