共和分の直感的な理解

---

参考文献:この記事は,統合の概念を直観的に紹介し,その基本的意味,その概念の動機,そして簡単な応用シナリオを理解するのに役立ちます.

• 統合概要

厳格な数学的な符号の定義や厳格な公式推論は含まれていない.

興味のある方は,ウィキペディアのCointegrationを参照してください.

なぜ平らになるのか?

統合という言葉は 安定性という意味にしかならない.

簡潔に言うと,平ら性 (stationarity) は,連続が時間とともに安定して変わらない性質であり,これは,データの分析予測を行うときに非常に好きな性質である.一組の時間連続データが平らであるということは,その平均値と微分が変わらないことを意味するので,我々は簡単にいくつかの統計技術を連続で使用することができる.平らなと非平らな連続が直観的にどのように見えるかを,まず一つの例を見てみましょう.

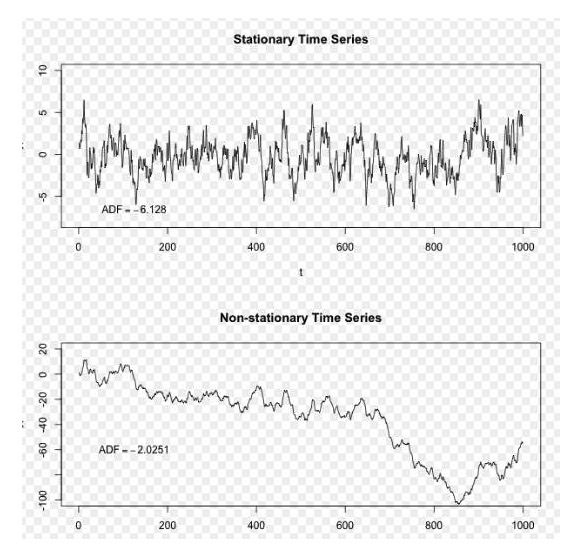
写真はウィキペディアより

上の図では,上位の順序は平らな順序で,それが常に長期平均値の周りに波動していることがわかります. 下位の順序は不平らな順序で,その長期平均値が変化していることがわかります.

応用例として,ある資産の価格序列 (または2つの序列の価格差) が平らである場合,その平均値から偏ったとき,その価格が将来ある時点でこの平均値に戻ることを期待することができる.この性質を利用して投資をすることで利益を得ることができる.ある株の長期平均値が9ドルで,現在の価値は8ドルであるとする.この株の歴史序列が平らな性質を持っていると判断し,この平らさが維持できると仮定すると,この株のみを購入し,将来の価格が9ドルに戻るまで待って,1ドルの利益を得ることができる.

株価の順序はこうです:

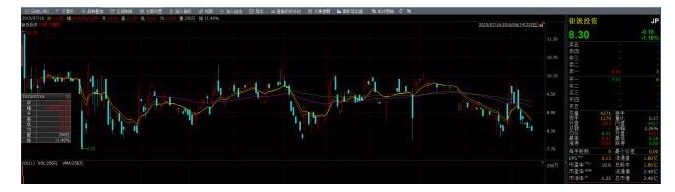
安定性は良いことだが,現実には,ほとんどの株式は不安定である.それでは,我々は平らな性質を利用して利益を得ることができるのか? 答えはイエス,このとき協調関係 (cointegration) が登場する!もし2つの配列が不安定であるが,それらの線形組み合わせによって平らな配列が得られるならば,我々は,この2つの時間配列データが協調的な性質を持っていると言う.また,我々は統計的性質をこの配列の配列にも適用することができる.しかし,指摘すべき点は,協調関係 (cointegration) が関連関係 (correlation) ではないということである.

例えば,二つの時間序列のデータセットの差が平らである場合,その差の平らさに基づいて投資利益を得ることができる:二つの株式の価格があまりにも大きく,平らさに基づいて,価格差が収束すると予想するので,低価格の株式を購入し,高価格の株式を空売りし,価格が戻ってくるのを待つときに逆操作を行い,利益を得ることができる.

パイアトレードとはそういうものです.

• 安定性と検査方法

厳密に言えば,平らさは,厳格に安定 (strictly stationary) と弱平ら (weak stationary) とに分けられる. 厳格に安定とは,一列が常に不変の分布関数を持つこと,弱平らとは,一列が不変の定数を持つ記述的統計量である.すべての強平らな平らな序列は弱平らな性質を満たすが,その逆は成立しない. 一般的に平らさは弱平らである.時間序列分析では,通常,単位根テスト (unit root test) を用いて,プロセスが弱平らであるかどうかを判断する.

応用例を挙げると

まず,一致関係は関係関係ではないことに注意を向けましょう.私たちは人工的に2つのデータセットを構成し,その結果,一致関係を直観的に見てみましょう. import numpy as np import pandas as pd import seaborn import statsmodels import matplotlib.pyplot as plt from statsmodels.tsa.stattools import coint

構造データ

まず,それぞれのデータ長が100である2つのデータ群を構成する.最初のデータ群は100と下向きの項と標準正規分布を加える.第二のデータ群は,最初のデータ群の基礎に30を加え,追加の標準正規分布を加える.

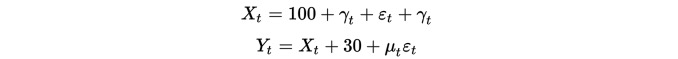
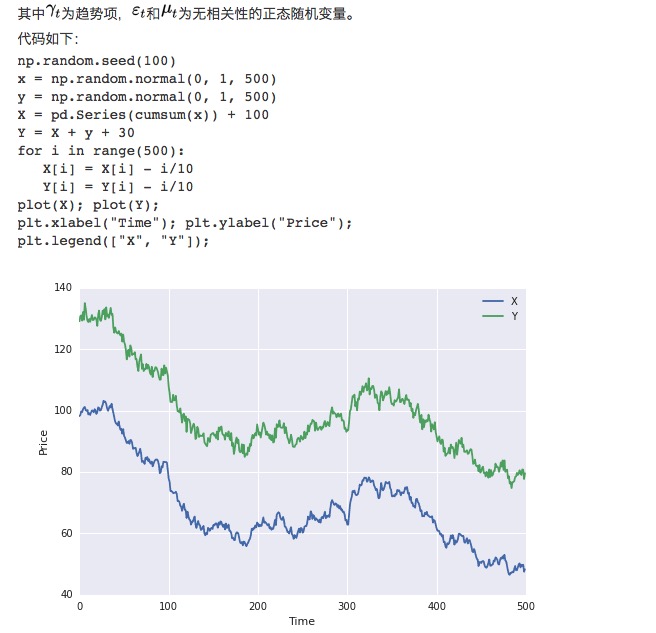
明らかに,この2つのデータセットは均等ではない,平均値が時間とともに変化するからである.しかし,この2つのデータセットは,その差列が均等であるため,整合関係にある.

plot(Y-X); plt.axhline((Y-X).mean(),color=“red”, linestyle=“–”); plt.xlabel(“Time”); plt.ylabel(“Price”); plt.legend([“Y-X”, “Mean”]);

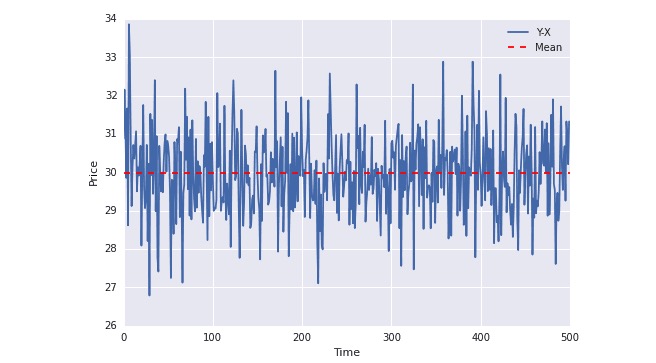
上図から,青い線が平均値の周りに常に波動していることがわかります。平均値は時間とともに変化しない (実際,差も時間とともに変化しない).

• 締めくくり

整合を数学的な観点から説明すれば,もっと複雑になり,将来の数学的授業に巻き込まれることになるだろう.我々は,単に (level-0) のレベルでの簡単な説明をしておいただけで,整合と実用的な応用を,よりよく組み合わせることを目的としている.

授業の質を測る方法について