リスク小史 (四) モフと神の曲線

前回の記事では,ヤコブ・ベルヌーリが亡くなった時,確率論に関する本棚の推測理論はまだ出版されていなかったと書かれていた.彼の手稿の整理の任務は,彼の甥のニコラス・ベルヌーリ2世 (早起きの天才) に委ねられた.ニコラスが叔父の遺言を完了した後,また,実際の確率の偏差レベルを,観測回数を決定した場合に研究したいと始めた.おそらく天才冥想中も,自分の努力が足りないと感じたので,モフーリを研究に招いた. モフ (Abraham de Moivre) は多くの場所でメフと訳されているが,彼の肖像を見た後,私は後者のこの翻訳法をあまり支持していない.この招待は,後世伝説の数 (ji) 学 (you) 界の良い話を成し遂げるはずだったが,モフは拒否した.そして,彼が拒否した理由は,彼はまだ十分な荒れ果てた力を持っていないと感じていたからである.

• ダンモフ モフは実はヤコブ・ベルヌーリよりわずか十代の若さで,彼の生涯は事実上小説で描写できる,それは悲惨な世界である.当時フランスはカトリックの雰囲気狂気の国であり,モフは偶然か偶然かプロテスタントであった.後にフランス国王ルイ十四世が,国内プロテスタントを劣等市民と宣言し,子供たちはプロテスタントに改宗しなければならないという法令を発令した.この套路は,フランスでプロテスタントを定性カルトにした.モフは,それゆえ2年間も投獄された.獄中からのモフは,イギリスに逃亡したが,彼は学界で教職を得ることはなかった.しかし,彼はニュートンとの友人であり,30歳の時にイギリス王室の会員であったにもかかわらず.モフは,平時,他の数学者や指導者に頼り,生活費を支えるために,日常の基本構成を数学で作る,そして,子供の遊びや罵りで作るという,その結果として,貧しいフランスに委託され,87歳まで生きていた.

しかし,私たちはここで声を出して,モフは永遠に不死になる! 1711年にモフは幸運を測るについてのを出版しました. もしその時に出版された本が腰の封筒を持っていたならば,その腰の封筒にはニュートンの推薦語が必ず書かれていたでしょう:,モフ先生に聞いてみてください,彼はこの点で私よりもよく知っています.

モフは,その頃はなかったので,あまりの版税を手にすることができなかった.

前回の問題 (リスク・ストーリー) を覚えておけばよいでしょう. ベルヌーリ少将は,の中の5000個の石に対して,25,500回のクレープをかけて,全体の石の割合を推定することができるでしょう. しかし,25,500回のクレープがあまりにも多く,石を1つ1つ倒すよりもはるかに多いこともわかるはずです. モフは,問題に対して非常に良い解決策を思いつきました. モフは,この方法が,数学の歴史をする奇妙な方法だと,謙虚に述べるつもりはありません.

微積分とパスカルの三角を用いたグループ抽選方法をとる.彼は,毎回100個の石をから取り出し,黒白の石の割合を記録し,再び石を入れ,また同じ抽出を行うと仮定した.この方法によって,モフは,あなたが記録した比率と実際の比率の近似偏差を事前にあなたに伝えることができ,そしてこれらの比率は,それらの平均値の周囲にどのように分布しているかを教えてくれる.

この言い方は,昔から知っているようなことなのか,口に浮かんだようなことなのか,すぐその名前を呼んでみたいということなのか? そう,これが皆さんがよく知っている正規分布である。正規分布の曲線は,鐘形曲線のようなもので,ほとんどの観測値が中央に集まって,すべての観測値の平均値に近づき,それから平均値の位置から対称的に両端に傾き,そして平均値の両端の観測値の数は等しくなる。最初は,曲線は高速下を傾いているが,両端では,このような傾きは平らになるので,平均値から遠く離れた観測値の出現の確率はより小さい。数年後,統計学の教科書で,この曲線について記述され,それをモルフォール極限センターと呼んでいる。

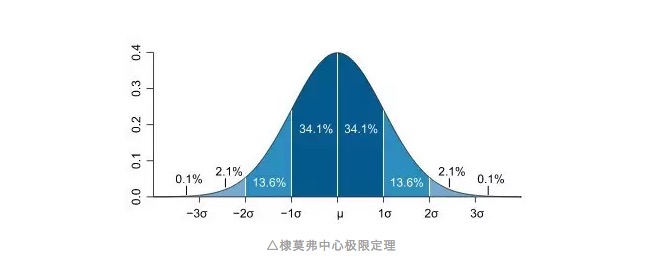
このようにして,標準差の概念を導入することができる.実際は,Public Issueの他の記事で (なぜ標準差なのか? 大神眼でリスクの測定) 我々はそれについてすでに言及している.標準差は,実際,観測値が平均から偏っている程度を表現する,あるいは,我々はそれを平均から偏っている単位として理解する.正規分布の場合,我々が抽出した100個のグループ1の石の比率は,約68%が平均の2側1標準差の範囲内に落ち,そして2標準差の範囲は,約95%の観測値を包含できる.

敬虔な信者として,モフは鐘形曲線を神の産物だと考えていた.彼の考えでは,このような測定によって,我々は不確実性を克服し,その結果,全てのリスクを征服することができる.なぜなら,曲線は,起こりうる全ての現象とその確率を記述しているからであり,おそらく偶然によって,いわゆる偏差が生じるが,時間の経過とともに,これらの偏差は,我々がまとめた法則に影響しないだろう.

モフの言葉を,皆が喜ぶように解釈すると,が失望するのは,たまに電話番号をダイヤルできないこと,何度も試して,いつも答えることである.中学校でも,古典的な課題がある (,なぜ私がいつも中学校の課題を使うのか).それは,製品の合格率についてである.もし,一群の製品について,業界標準が,廃棄物の割合が0.1%を超えないことを合格であると考えるならば,それは,私たちが製品から無作為に10000個を選び,その中の廃棄物が10個を超えないならば,合格していることを意味する.しかし,結果として,この10000個のうち,最後に12個が現れた.平均的に言えば,製品の廃棄物の割合は0.1%であり,実際には,モフの方法を利用して,12個の廃棄物の出現の確率は何であるか計算することができる.

しかし,この問題は,ほとんどの場合,私たちにとって無意味です. なぜなら,実際には,製品の平均廃棄物の割合がどのくらいになるのか,平均廃棄物の割合が検定基準より高い場合,私たちの製品群が検定を通過する確率はどれくらいでしょうか? もし20,000の製品を抽出して検定を行うならば,その10,000の製品の結果は直接利用できるでしょうか. これらの問題は,モフの曲線で説明するにはあまりにも面倒すぎるようです. だから,ベイエスの名前は,すべての統計学と博学教科書に現れるでしょう,これが私たちの次の記事の内容です.

中国量化投資学会より