著作権声明:この記事のコードを転載する場合,出典を注記してください. 商業的目的,論文の作成の場合,私的な手紙または [email protected] の著者へ連絡してください.

1. はじめに

量化取引の利点

定量取引は,高度な数学モデルを代替して,人間の主観的な判断を指し,コンピュータ技術を利用して,膨大な歴史的データから海選が余剰利益をもたらす可能性のある多種多様な確率事件を策定し,投資家の感情の波動の影響を大幅に軽減し,市場が極端に狂気や悲観的な状況で理不尽な投資決定を避ける. デジタル通貨の普及により,世界各国の金融機関が,*7時間連続した取引市場の連続性,および定量取引は高周波取引の効果を達成することができる.デジタル通貨市場の開始は明らかに定量化の良いスタートである. 現時点では,デジタル通貨市場はまだ未熟である. プラットフォーム取引システムの障害,k線插座は,時折発生し,定量取引のリスクである.

GQNRモデル概要

         このモデルは,Garchモデルに基づく波動率予測であり,分位数回帰による波動率を予測するVaR値を進めて,非線形回帰を利用し,例えば,GAが,将来の次の周期における上限VaRと下限VaRを予測するためにフィーミングを行う.この方法モデルは,後述でGQNRと呼ぶ.

1. ガーチモジュール

       このセクションでは,この戦略のGarchの核心推論を詳細に説明します.この方法は,金融市場において一定の普遍性を持ち,デジタル通貨において一定の予測効果に達します.

1.1 ガーチの定義

       ARCHモデルの本質は,残差平方序列のq級移動平面を,当時の差異関数値に適合させるものである.移動平均モデルが自相関数q級切尾性を持っているため,ARCHモデルは,実際には,差異関数の短期自相関数のみに適用される.           しかし,実用的には,残差配列の異方差関数が長期にわたって自在であるため,ARCHモデルに適合する異方差関数を使用すると,非常に高い移動平均階数が生み出され,パラメータの推定が難しくなり,最終的にARCHモデルの適合精度に影響する.                                                                                                                                                                         GARCHモデルは実際にはARCHの基礎で,差異関数を考慮するp級自帰性により形成され,長期記憶を持つ差異関数に効果的に適合することができる.ARCHモデルはGARCHモデルの一例であり,p=0のGARCH (p,q) モデルである.

1.2 ARCHプロセス

      の定義は,σnは,n番目の取引周期で資産の波動率を推定し,muは日利率であるので,最近のmの取引サイクルでの収益率に基づいて偏りなく推定することができます: $\( \sigma *n^2= \frac{1}{m-1} \sum\limits*{i=1}^m {( { \mu_{n-i}- \overline{\mu} } ) ^2}, \)\(        を次の変化に変換する. 1はμn-iを百分比利率に変換する. 2はm-1をmに変換する. 3はμ=0と仮定し,これらの変化は結果に影響を及ぼさない.上記の式に従って,波動率は簡略化できる. \)\( \sigma *n^2= \frac{1}{m} \sum\limits*{i=1}^m { \mu_{n-i} ^2}, \)\(        つまり,各周期の波動率の平方は等重量1/mを持つ.現在の波動率を推定するので,近距離のデータにはより高い重量を与えられるべきであり,上式は次のように変更できる. \)\( \sigma *n^2= \sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)$         αiは第 i 取引周期の利回り二乗の係数であり,正値を取ってiが小さい値が大きいほど,重量の和は 1 である.さらに推移して,長期差率VLが存在すると仮定し,対応する重量はγであり,上述の式により得ることができる:

\[ \begin{cases}\sigma *n^2= \gamma V*{L}+\sum\limits_{i=1}^m { \alpha_i\mu_{n-i} ^2}\ &\ \gamma+\sum\limits_{i=1}^m{\alpha_i\mu_{n-i}^2}=1 & \end{cases} , \]

       令ω=γVL,公式(15) は次のように書き換えることができる. $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)\( 上の式から,一般的なARCH () 1のプロセスが得られます. \)\( \sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2}, \)$

1.3 ガルチプロセス

         GARCH (p,q) モデルは,ARCH (p) とEWMA (q) モデルの組み合わせであり,波動率は前p期の利益だけでなく,自身前q期にも関係しており,次のように表される. $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}+\sum\limits_{i=1}^m { \beta_i\sigma_{n-i} ^2}, \)\(       上記式から,一般的なGARCH ((1,1)) を得ることができます. \)\( \begin{cases}\sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2+\beta\sigma_{n-1}^2}\&\ \qquad\alpha+\beta+\gamma=1 & \end{cases} , \)$

2 QRモジュール

        このブロックは,戦略的分位数回帰の重要性について説明します.

2.1 QRの定義

       分数帰帰帰は,帰帰変数Xの集合と,解釈される変数Yの分数の間の線形的関係を推定するモデリング方法である。           過去の回帰モデルは,実際には,説明される変数の条件期待を研究している.また,説明される変数の分布の平均数と分数の関係も懸念されている.これは,1978年にKoenkerとBassettによって最初に提唱された.OLS回帰推定量の計算は,最小残差の平方根に基づいている.分数回帰推定量の計算は,非対称的な形式の絶対残差の最小根に基づいている.この中で,中位数回帰は,最小絶対差の推定値 (LAD,least absolute deviations estimator) を使用している.

2.2 OLSからQRへ

        一般的な回帰方法は最小二乗法である,すなわち最小化誤差の平方和である. $\( min \sum{({y_i- \widehat{y}*i })}^2 \)\(        分数の目的は,上記の式に基づいて重加された誤差の絶対値と最小化することです: \)\( \mathop{\arg\min*\beta}\ \ \sum{[{\tau(y_i-X_i\beta)^++(1-\tau)(X_i\beta-y_i) ^+ }]} \)$

2.2 QRビジュアル化

戻り線が異なる空間に分けられ, 戻り線が分岐線になります.

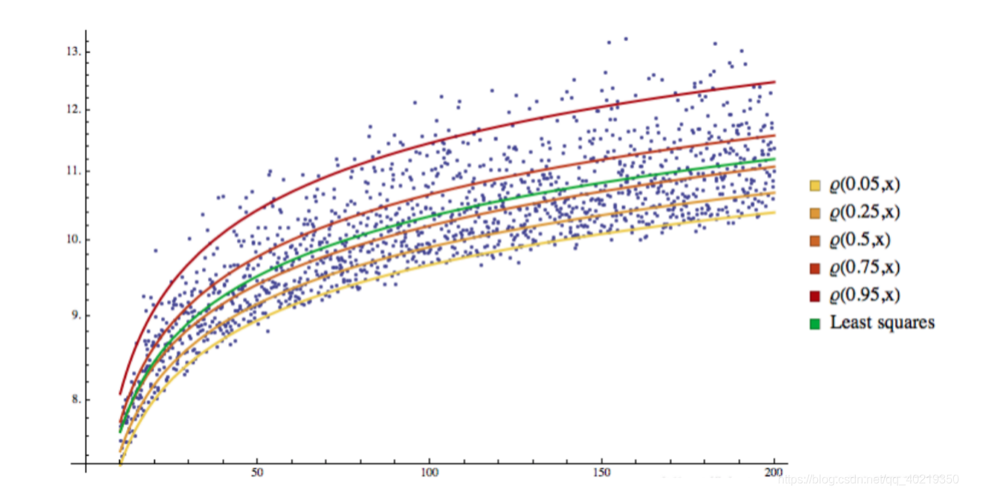
3. GARCH-QR回帰

        市場未知波動率シグマと分数Q (VaR) を回帰して,将来の概率の状況下での波動的下落を予測できるかどうか,私たちは自然に考えます. この部門は,この方向に進みます.

3.1 波動率とVaRの回帰形式の選択

戦略の核心に触れているので,ちょっとした形式で説明します. $\( VaR=\epsilon+W^TE\E=(\zeta,\zeta^2,\zeta^3,\zeta^4)\W=(W_1,W_2,W_3,W_4) \)$

3.2 ターゲット関数を定義する

        上記の情報に基づいて,組み合わせた結果,最終的な最適化対象関数が得られます. $\( \widehat{W}=\mathop{\arg\min_W}\ \ \sum{[{\alpha(VaR_t-W^TE_t)^++(1-\alpha)(W^TE_t-VaR_t) ^+ }]} \)$

3.3 機械学習によるターゲット関数の最適化

このステップは,従来の梯度が下がり,遺伝的アルゴリズムも利用できるので,読者は自分の創造性を発揮して実験することができます.ここでは,別のブログで詳細に説明されていた,最適化されたGAアルゴリズムを使用しています.ゲノムを定義する

GQNRを量化する方法

1. アイデアの定着

       GQNRの核心は,市場の波動率であり,各期間の現在の時間点において,GARCHによって次の期間の波動率の予測を予測することができる.また,過去データによる波動率の予測分数回帰により,大概率の場合には超えない波動の値の上限と下限を入手することができる.そして,この2つの境界は,全体の核心である.上限を触れたら,大概率の短期下には回調の傾向があると考えることができる.下限を触れたら,大概率の場合には短期下には上昇の傾向があると考えることができる.

2. 難しさ

• 復元の形をとる
• 適応アルゴリズムの選択
• 機械学習の適切なパラメータ
• 市場の不確実性やランダム性

3. 解決策

• 戦略を学ぶ時間を短縮する
• 長期リスクに対する 単一預金保証金の低減
• 双均線トレンドの共同検証と二次減值確認の追加