ギャンブラーの取引戦略

この記事の実践的な内容は,マーク・ウォルバーグの最新作『ザ・ギャンブラー』 (2014) を参照してください. この記事の主題は,ジョブズが言った言葉です. “私たちはランダム性を減らすことで,人々がもう少しランダムに感じられるようにします (Were making it less random to make it feel more random) “.

記者は,前文を読んで,その後に本文を読むことをお勧めします.

• ##### アメリカ独立宣言の中で最もよく使われた言葉は”すべての人は平等に創造された”である.しかし,これは事実の陳述ではなく,私たちの祈りの祈りの願いに近いものです.私たちはすべての人が平等に創造されたことを願っています.

願望は存在していないことを暗示する:誰かが赤ちゃんの車から奔を運転し,誰かがIQ180で,3歳の時に毛筆で微積分を計算し,痩せた金体を書き出す.

格差の問題は,上記よりさらに不均衡です. なぜ,いつも誰かが賞を勝ち取るのか?

会社にはいつも何人かいる,毎年抽選会で賞を台に投げかけ,幸運に恵まれると言うのは当然だ. 私はコーヒーの中で1送1買って,開けて,また1送1買って,夜興奮して眠れなかった (もちろん,カフェインも飲みすぎたかもしれない).

この経験は”連続受賞”と言えるものです.

連続受賞は不公平で,いつも他人の母親に起こる.

会社に200人の従業員がいて,年次抽選で優勝する確率は1/200=0.5%で,2年連続で優勝する確率は0.5%×0.5%=100万分の25で,かなり低いですね。

しかし実際は,この数字は,あなたが2年連続で優勝する確率です. 200×0.5%×0.5%=0.5%です. これは,あなたが抽選で優勝する確率と同じです.

3年以内に1人が2回受賞する確率は:1 - 3年以内に3つの異なる受賞者による確率=1-200×199×198/[200×200×200]=1.5%

3年以内に1回優勝する確率とほぼ同じだ。言い換えれば,あなたが3年以内に1回優勝するなんて,私に1回賞をあげても不十分だと思ったら,台下で他人に3年以内に2回優勝するなんて,合理的だ。

年間会場を吸うだけでいい

五月大賞の受賞者より,同じ年会で連続で受賞した人物が,五月大賞の受賞者だと考えるのは,もっと恐ろしいことでしょうか?

200人の会社の例に戻ると,10個の賞があると仮定すると,従業員は賞を繰り返し得ることができます. 1−10個の賞を10人の異なる人物が獲得する確率) =1−200×…×191/[200×…×200]=20.4%

賞を貰った同僚があなたに言う可能性は5分の1くらいある…少し酸っぱいですね.これは生来不平等ではなく,誰もがチャンスを持っていることであり,今回はあなただけではありません.

ロンドンのトレーダー:ポイントが来た

ランダムでないランダム

このはあまりありえないように見えるが,実際は,人生でこんなにもありえない現象である,即ち,無作為に歌をプレイリストから削除しない限り,無作為に歌をプレイリストから削除しない限り,10曲のプレイリスト,一度に無作為に歌をプレイしたい場合は,10曲しか聴いてない!/1010=0.036%,不可能のタスクの確率よりも低い,またトム・クルーズの離婚しない機率よりも低い。無作為に歌をプレイリストから直接削除すれば問題解決できるが,欠点は,少なくとも1曲を10回聴いてから2回聴くことだ。

Appleのランダム再生プログラムは,異なる歌手,異なる曲調を交互に再生し,ユーザーに各曲の間の無関係さを感じさせると言われています.ジョブズは”我々はランダム性を減らして,それによって人々が少しだけランダムさを感じさせています.

• #### 準備が整ったので,今から正文を書き始めましょう.

取引に関するギャンブラーモデル (具体的実例は,マーク・ウォルバーグの最新作『ギャンブラー』 (The Gambler) を参照してください.しかし,ロンドンのトレーダーは,この映画があまり好意的ではないと述べています)

取引の時には,いつでも方向を推測し,間違えたら反転して倍増し,再びポジションを開く,価格は必ず戻ってくる,それは不可能です. 路上で上昇し,戻らない (下降し,戻らない) は,私は毎回倍増し,再び戻ってくる,私は本+お金を勝ち取った.

負けたら1ドルでも構わないで,次は2ドルを賭けて,勝ったら4ドル,もう1ドル,また間違ったら4ドルを賭けて,返って8ドル,合計1+2+4=7,つまり1ドルを賭ける.

計算がうまくいけば,あなたはそれを知る必要もないし,毎回1円を貯める.

やってみよう! やりなさい! やりなさい! やりなさい!

しかし,この古典的なギャンブラーズ (ギャンブラーズ) の誤謬は,ポンチス (ポンチス) の詐欺のように,驚くべき活力を持ち,長期間,揺るぎない,揺るぎない,一世代から一世代へと,投機家をだます.

投げられたコインの正の確率または期待値は0.5であるが,ただ一度投げられた場合,正の確率は0か1である (遠距離偏差0.5).投げられた回数 (つまり,サンプルが大きくなる) の増加とともに,正の確率は徐々に0.5に近づく.しかし,認知心理学の小数法則 () によると,人は通常,サンプルサイズの影響を無視し,小さなサンプルと大きなサンプルが同じ期待値を持っていると考えます.

ポジティブなことがたくさん出てきたら 逆に悪いことが起こる可能性が 増えたように感じる.

輪盤ののテーブルでは,赤が連続して何度も登場した後,常に多くのギャンブルが黒に重点を置く.

この戦略を用いると,資金の曲線は次のようになる:

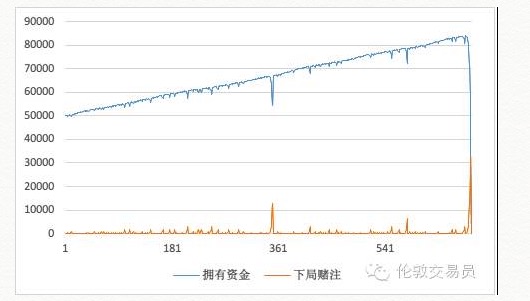
実践すると,資金の曲線は上向きで,安定しているように見えます. 361回近く実践すると,失敗の連続が見られます. そして,この戦略に固執すると,利益が戻るだけでなく,上向きに上昇し続けます.

もちろん,このような戦略の最終的な帰着は,無償で,無償で,そして,夢の破綻の激しい苦痛を伴うものです.

私はこのようなことを何度か経験したことがある. 取引の新アイデアが発表され,ほとんど撤回されないたびに, ギャンブラーに騙されたのではないかと疑問に思う.

ギャンブルに夢中になった人は,そのまま逃げられないのです. 格子取引の戦略,マーティン・ゲルガ・ギャンブル法など,決してギャンブルの誤った手から抜け出せません. しかし,それは永遠の生命の力を持つことは間違いありません.

戦略の流行は,その収益能力ではなく,その人格に合っているかによって決定されるからです.

この世にあるものは,人間の期待に応える限り,強固な生命力を得るようである.パンチス詐欺のように. 格子戦略も良い,マーティンゲル戦略も良い,最初は,常にあなたに非常に安定した報酬を与える. 期待する.そして,資金の引き戻しは無い.

人間の脳は,利益よりも損失を嫌う.これは,人間の祖先が,草原の祖先が,遠い将来のことを考えず,腹を空かせて,この食事を終わらせるため,古代から進化した戦略です.

しかし,人類の文明は急速に発展し,日増月増し,生物学的意味での脳は,依然として百万年単位で進化している.古代の脳は,どのように今日の金融市場に対処できるのでしょうか.したがって,自分の主観的な感覚に基づいて市場を判断したり,戦略を判断したりしないでください.感覚ではなく,人間の知識に依存する必要があります.

ニューロエコノミクス (第二版)

資金管理を主な取引ルールとして,市場に対する洞察を必要としないという自信を持って, 安定した,不損な取引戦略が推奨されているなら, 気をつけましょう. 詐欺師の誤った考えの別の新着である可能性が高いです.

金融市場は熱力学のようなシステムで,その結論を心に留めて,騙されないようにしましょう.

エネルギー保存法則は,エネルギーが空から生まれ,空から消えることはないということです. 市場において,あなたが何か貢献や洞察を行わず,市場をより効率的な資源にしない限り,空から利益を生むことはできません. これは自然の法則に反しています.

どんな戦略も自然法則に逆らえないことは確かです. 効果的な戦略には,情報不均衡の優位性,超人的な洞察力,あるいは自分のリソースを活用して市場を効率化することが必要です. 市場があなたに報われるためには,あなたがそれに応じて貢献する必要があります.

ネットワーク取引戦略 ((間違えば倍増する) は,出力を提供せず,利益を得るという妄想は,永続的な動機を作りたいというように,必然的に愚かな夢を見ることである.

取引コストを考慮しない場合,格子戦略 ((気軽に1つの方向を行って,平仓を決して止まらずに損なう,一度正解したら,すぐに現金化して,一度間違ったら,逆転して,ポジションを倍増する。) の予想収益はゼロ。

予想される収益は0で,取引コストを考慮すると,予想される収益は負です.

また,ネットワーク戦略は,追加投資が必要と,利回りモデルに合致するものであることを考えれば,数回の失敗の後,新たな投資が必要となる資金は天文学的な数字になります.

資金調達能力は,結局のところ,上限があり,その制約があるため,あまり素晴らしい下場は必然である.

理性のある人なら誰でも理解し,堅持する,しかしそんなに難しい。

しかし,しかし!!! 天にパンがないなんて言って,みんなががっかりした様子で,ギャンブラーたちの誤りを理解したあと,チェスの1つ技を上した賢い人が何なのか見てみよう.

ツイッターでは,この発言を”人人ネット”のユーザーから引用しています.

シンプルな機械装置で,黒と白を代表する2つのコイン口がある.プレイヤーは,それぞれ賭けたゲームコインを入れている (ゲームコインと1ドルの現金相当).すべてのプレイヤーのコインが終わるまで待って,機械が動作し,ランダムに黒と白の2つの小さな穴からボールが落ちます.敗者は空き,勝者は賞金2倍になります.

S君,ここで,私は,この局は,ボスが1/2の相互排斥事件に対して1の確率を賭けていると言うのと同じだと気づきました. このモデルでは,プレイヤーはどんな混合戦略をとっても,期待される利益は常にゼロです.

勝ったとは思いもしなかったし,勝てる可能性もなかった.

S君はその後,彼の戦略は単純であると言う.すなわち,黒のような色を選んだとき,最初に黒に1枚を押す.負けたら,二度目に2枚を押して黒を続ける.また負けたら,三度目に4枚を押して黒を続ける.

この方法の利点は,前回の損失が何であれ,次の勝利で,損失をに変え,純利益1元に変えることができ,n回連続で失敗する確率は非常に小さい,わずか1 / … 2 ^ n) であった.

もちろん,この方法では,私を騙すには十分ではありません. 混同策の期待はゼロだと私が言ったとき,自然にこの策も含まれています.

この戦略は,負ける確率が小さいように見えますが,なぜ期待はゼロですか? 簡単です,彼の賭けがあまりにも大きいので,最初の7回をすべて負けたと仮定すると,第8回には256ドルを押さえて転倒する可能性があります. しかし,第8回に負けたら,累積損失は511ドルで,私は初中生Sが継続する資本はないと思います. 言い換えれば,失敗の確率は小さいが,小確率の事件が7回または8回発生するたびに,損失は致命的であり,数週間にわたってゲームを続けるお金がありません.

率直に言って,私はこの戦略の実行可能性に非常に疑問を持っています.

ギャングの誤りの一般的な形態である, 格子策のような単純な策である,と理解できる. ギャングの誤りである,と理解できる.

しかし,S君はこの戦略を実際に採用し,ゲームルームで20〜30コインを稼いだ後,午後は他のゲームで遊んでしまった.私は彼の一面的な言葉を完全に信じただけでなく,彼の後の分析は,私の以前の分析が致命的な間違いを犯したので,この戦略が実際に機能していることを信じなければならなかった.

漢平,君の致命的な過ちは…君は完全に公平なゲームだと信じてる.

面白いところは,スーパー干し物です.

とはどういう意味ですか?

S君は笑って言った”,あなたの分析は数学的に全く間違いない.しかし,あなたの結論は,プレイヤーの期待がゼロである,つまり,庄主の期待もゼロであるということを忘れないでください.しかし,庄主の利益は本当にゼロですか?もしゼロなら,彼はこの機械を借りて,この賃料を損しているのではないですか?”

実際,S先生の考えは,庄者が必ずお金を稼ぐだろう,と私は考えていました。唯一の方法は,庄者が小球を操っているということでした。極端な仮定をすると,もし誰かが白に1万を打つならば,彼が勝つ確率は非常に小さいでしょう,庄者は数週間の流水付の東流をじっと見守らないでしょう。ゲーム機屋で1万を稼ぐ人はいませんが,S氏によると,一度に200〜300を稼ぐ成人の土豪は珍しくありません。

宝くじ屋にとって,最も貪欲な状況とは,毎回小さなボールが,より小さな賭けの色に落下することを操作すること以上に,毎回勝つことではない.しかし,これは明らかに正常ではない.もしそれがあまりにも明白でプレイヤーに認識されれば,楽しい遊びはできない.

勝負があるべきで,全体的に適切な小利益を維持する,例えば10局ごとに10%,大きいとはいえないが,金融理財製品に比べれば大利益だ.

遊びに来たとき,いつも少数派を味方にするのは,あなたの戦略じゃないですか?

Sはさらに,この機械の設定は,各プレイヤーが先行してコインを投げるものだと述べています. プレイヤーと交流しなければ,基本的に他のプレイヤーがコインを投げた場所を見ることができません. そして,毎回他のプレイヤーと交流して決断することは不可能です.

(笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑)

S: 孤立して考えられないんだ. 潜入ルールがあるんだって 気付いた時,もうずっと前に進んだんだんだ.

勝った数人だけでも,上司にお金を稼ぐのに十分だと思っています.

S:のボスは,事前にマシンと場地のコストを負担しており,つまり,彼はこのゲームで負債を負担している。彼は負債を負担できないだけでなく,儲けなければならない。そして儲けには2つの必須条件がある.一つは,誰かが一度に巨額の金を奪うことができないこと,これは少数派勝利である,しかし,もう一つ重要な条件は,が安定した収益の前提でできるだけ多くのプレーヤーを引き寄せることである。

ギャンブラーにとって,この賭博は税金を払わなく,勝負は半々に見えるが,実は非常に魅力的だ.

S:ええ,でも数学的な考えを持たない他のプレイヤーはそうは考えません.さて,最初の質問に戻りましょう.私の戦略は失敗する可能性が低いが,失敗すれば,大きな損失を伴うと言っていましたね.

失敗する確率は1/2^nですが 失敗すると2^nくらいの損失になります. 期待はゼロです.

S:ああ,私が負けるかもしれない状況についてよく考えてください。私の手には通常300円くらいがあり,1枚のプレッシャーから128円まで支えるだけの金がある,つまり8回のプレイです。私が負ける唯一の可能性は,連続8回のプレーが白色で,それで終わりです。ああ

(笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑) (笑)

S:ああ,あなたは間違っています,このような確率は数学にしか存在しません.実際には,ボスがこのような状況を許さないことは絶対にできません.ゲームで,同じ色が8回現れるのを想像してみて下さい.私の場合,もちろん受け入れられます,私は何千回もプレイしているので,白の確率は1/128です.

ゲームが操られていると疑わないようにするには,ゲームが操られていると疑わないようにするには,ゲームが操られていないと疑わないようにするには,ゲームが操られていると疑わないようにするには,ゲームが操られていると疑わないようにするには,ゲームが操られていると疑わないようにするには,ゲームが操られていると疑わないようにするには,ゲームが操られていると疑わないようにするには,ゲームが操られていると疑わないようにするには,ゲームが操られていると疑わないようにするには,ゲームが操られていると疑わないようにするには,ゲームが操られていると疑わないようにするには,ゲームが操られていると疑わないようにするには,ゲームが操られていると疑わないようにするには,ゲームが操られていると疑わないようにするには,ゲームが操られていると疑わないようにするには,ゲームが操られていると感じるようにするには,ゲームが操られていると感じる必要があります.

この原理に基づいて,正常分布の小さな確率の事件でさえも取り除かねばならない,なぜなら,それらは疑いを引き起こすからである (公平だから不公平だと感じられるからである).逆に,温水煮青のような偶発的な操作で数盤の少数者が勝利する,なぜなら,庄主も事前に白と黒のどちらかが少数であるということを知らないから,結果的に見れば,黒と白の平均分布を破壊することはないからである.

庄家はそのようにして,少数の勝者に勝てることを恐れず,このトリックは直感的に黒と白のバランスを破らない.しかし,同じ色のが連続して何度も出現することは絶対に許されない.しかし,多くのゲームでこのような小さな確率の出来事が起こるのは当然である.

数学では小確率の事件ですが,現実ではゼロ確率の事件として修正されています.

この話から,Sが本当に鋭いところを,そして,なぜこのような単純な戦略が,このような公平なゲームで,常に勝てるのかが,理解できたのです.

その後Sは,ボスが意図的に10%の収益をコントロールするのは面倒すぎると考え,結局ボスは他のゲームやプレイヤーも世話しなければならない.だから,より現実的な推論は,この機械自体がランダムな分布を備えているということだ.この分布の下では,ボスの収益は,プレーヤー全体と同じで,ゼロである.そして,ボスは,毎日しばらくの間,いくつかのゲームを操り,これらのゲームでボスが常に十分なお金を稼ぐようにして,他の時間は機械を自動的に動かせている.このようにして,誰かが万万を圧迫しない限り,このような状況でボスは大敵である.この公平な機械は,宝の盆である.

Sの策略は,貪欲な上司に対してのみ有効ではなく,見かけが公平な機械に対しても同様に試行錯誤する.その理屈は単純で,それは十数年前の機械で,その中に電子部品は確かにあったが,それ以上にそれは単純な機械装置だった.実際には,コンピュータを含む,機械を作った者は誰も,実際にのランダム性を表現することができなかった.どんなプログラムでもランダムな数は,本質的に複雑な計算下での偽ランダムである.もちろん,コンピューターの計算能力が非常に強かったため,それは非常に強大なランダム性を生み出し,何百万もの状況を模倣することができる.

しかし,単純な機械では,数十の状況をシミュレートするには大きなコストが必要であり,この機械がブラック・ブラック・ブラック・ブラック・ブラック・ブラック・ホワイト・ブラック・ブラック・ホワイト・ブラック・ブラック…白白白白白の5回のゲームの全部分,つまり2^5=32の状況を予備して持っていると仮定する必要はありません.これは,Sを除いて偶発的にプレーするプレイヤーにとって,十分なランダム性と公平さです.

Sにとって,この32の確率を予備して繰り返し呼び出すと,彼の戦略は5回の賭けを準備するだけで1+2+4+8+16=31元で常に勝利する.

実際,Sは最初の引き出しで30枚以上のコインを購入した.毎回,これらのコインを資本として使って,追加の20〜30コインを稼いだ後,本当にプレイしたいゲームに遊びました.つまり,マシンの予備金は32時間未満のケースです.

この時点で,私は,Sと私の思考の格差がどれほど大きいか気づきました.私の判断はすべて数学に基づいています.この部分は,前200~300語の解決は,無事に議論できます.しかし,後数千の単語は,Sが本当に考えている領域です.

このビデオを初めて見たとき,私は,まるで,の頂上を灌しているかのように,胎児の骨を切り替えました.

デジタルで構成された量的な世界の中で,より高い収益を期待する戦略を模索し,目の前にある,非常に大きな基本的な事実を無視しています.

投機取引は,血と肉との人間とのゲームだ! 量化は常に手段と方法に過ぎない,トレーダーは,結局のところ,人と取引しているのだ. 取引と呼ばれるものは,取引相手とあなたが完成したものだ. 投機市場は,人とゲームである,アルゴリズムではない. だから,ロンドンのトレーダーは,機械が機械に優れていることをさせ,人間に優れている部分を残すように常に強調している.

このことを理解すると,次の言葉は理解しやすいでしょう.

Sは,時には緊急事態や他の理由により,貯めたゲームコインを花灯して帰るしかなかったと言います。彼はほとんど上司に残ったコインをお金に交換させることはなかった (原則的には許される).。しかし,彼がこの戦略を繰り返し使用することを考えると,実際には小利を貪って上司を疑わせることは許されません.彼は数学的に明らかに負けるゲームコインを迅速に失ってしまいます。もちろん,偶発的に少し小銭を稼ぐこともあります.初三の店が突然倒産するまで,ボタンの上の30以上のゲームコインを手にし,また数十ドルも稼いだのです.結局は,主に楽しみのためであり,お金を送るためではありません。

これはSの物語です.

賢明なSさんは,上司が持っている情報優位性を理解し,取引相手のカジノのオーナーとして,このゲームを中止する権限を持っている.賢明な戦略は,見事に受け取ることである.

競争相手を優位にするのは,より高いレベルであり,利益を得るのは,異なる見解である.

虚しい利益を得たいという願望が 騙される根本的な理由である.

この世界には,価格の動きを判断せずに,利益を得る戦略があるのでしょうか?

しかし,成功するのは,努力によってではなく,貢献によってなのです.

例えば,ロンドンやニューヨークの金,そして上海の金には全く同じ化学性質がある.

しかし,両者が異なる取引所で取引しているため,のクロスマーケット・スレートと呼ばれる戦略が生じます.この戦略はの1価格法則を利用しています.つまり,同じものは,同じ瞬間に1つの価格しかあり得ないのです.

取引上の優位性を有する機関は,ITと資金上の優位性を利用し,価格が偏った時に先駆けして,高価格の黄金を空売りし,比較的低い価格の黄金の製品を作ります.IT技術と高周波戦略の競売方法については,記事を参照してください.

価格が必ず戻れば,このポートフォリオ投資は利益を得,黄金の将来の上昇または下落を気にせず,利益を得ることができる. (もし黄金の未来が上昇すれば,低価格でより多くの黄金を稼ぐには,高価格で空白するポジションの損失を余分に必要とする,その逆)

市場を効率的に支援し,それなりの報酬を得るために,自社のリソースを投入しているからです.

“天からパンを降らせない”

ロンドンのトレーダーが繰り返し強調しているように,もしあなたがこのビジネスについて,あなたの優位性,なぜあなたが必要なのか,あなたの上限がどこにあるのか,そして,なぜ利益が得られないのか,はっきりと分かっていなければ,この取引はしないでください.

取引が決まっていないか,やらないか,タイミングで止まるよりましだ. 取引が決まっていたら,問題があったり,タイミングで止まったりすれば,それは生存の前提だ.

• ### 結論から言うと:

ポンチ詐欺の爆破点に洞察力がない限り,いわゆる”贈与”や”返済”のような策略が本当の利益をもたらすとは考えないでください.

高利率の約束には疑問がつきものです. 投資の方向性を把握していない人は慎重に注意してください.

格子型の戦略のように,撤回策がないので,少し気をつけましょう.なぜこのような良い結果が得られるのか,何が優れているのか? 他の人が持っていないリソースや知識を持っているのか?

市場が求めるのは,何か特別なアイデアや資源がない場合です.

(この記事のソースはロンドン・トレーダー)