データ駆動技術に基づくペア取引

データ駆動技術に基づくペア取引

パア取引は,数学的分析に基づく取引戦略を策定する良い例である.この記事では,ペア取引戦略を作成し,自動化するためにデータをどのように使用するか示します.

基本原則

投資目標 X と Y のペアにいくつかの潜在的な接続があるとします.例えば,ペプシ・コーラ と コカ・コーラ のような同じ製品を生産する2つの会社がいます.あなたは,両社の価格比またはベース・スプレッド (価格差としても知られています) が時間とともに変化しないようにしたいと考えています.しかし,投資目標の大きな購入/販売オーダーや,企業の1社の重要なニュースへの反応などの供給と需要の一時的な変化により,両ペアの価格差が時によって異なる可能性があります.この場合,ある投資対象は互いに相対的に上昇し,もう1つは低下します.この不一致が時間の経過とともに正常に戻ることを望む場合は,取引機会 (または仲介機会) を見つけることができます.そのような仲介機会は,デジタル通貨市場や国内商品先物市場,例えばBTC とハブラン間の関係など,どこにでも見ることができます. 安全な資産の種類であるソヤフューチャーとソヤ油の間の関係.

臨時的な価格差がある場合,優れたパフォーマンス (上昇する投資対象) を有する投資対象を売却し,劣ったパフォーマンス (低下する投資対象) を有する投資対象を購入します.優れたパフォーマンスを持つ投資対象の減少または劣ったパフォーマンスを持つ投資対象の上昇,または両方によって,最終的に2つの投資対象間の利回りが低下することを確信しています.このすべての類似した状況において,取引は収益を上げます.投資対象が価格の違いを変えることなく,一緒に上昇または減少した場合,あなたは利益を得たり損ねたりしません.

したがって,ペア取引は市場中立な取引戦略であり,トレーダーはほぼあらゆる市場条件から利益を得ることができる. 上向きの傾向,下向きの傾向,横向的統合など.

この概念を説明してください. 仮設の2つの投資目標

• FMZ Quant プラットフォーム上で研究環境を構築する

まず第一に,スムーズに作業するためには,研究環境を構築する必要があります.この記事では,FMZ Quantプラットフォームを使用します (FMZ.COM) の研究環境を構築し,主に便利で高速な API インターフェースとこのプラットフォームのよくパッケージ化された Docker システムを後日利用します.

FMZ Quantプラットフォームの公式名称では,このDockerシステムはDockerシステムと呼ばれています.

ドッカーとロボットの展開について 私の前の記事を参照してください:https://www.fmz.com/bbs-topic/9864.

ドーカーを展開するために独自のクラウドコンピューティングサーバを購入したい読者は,この記事を参照してください:https://www.fmz.com/digest-topic/5711.

次に,Pythonの現在の最大のアーティファクトをインストールします. Anaconda.

この記事で要求されるすべての関連するプログラム環境 (依存ライブラリ,バージョン管理など) を実現するために,最も簡単な方法は Anaconda を使用することです.これはパッケージ化された Python データサイエンスエコシステムと依存ライブラリマネージャです.

アナコンダのインストール方法については,アナコンダの公式ガイドを参照してください.https://www.anaconda.com/distribution/.

この記事では,Python科学コンピューティングにおける 2つの人気のある重要なライブラリである numpy と pandas も使用します.

上記の基本作業は,Anaconda環境とnumpyとpandaライブラリを設定する方法について紹介する私の以前の記事にも言及することができます.詳細については,以下を参照してください:https://www.fmz.com/bbs-topic/9863.

次に,コードを使って 2つの仮説的な投資目標を実装しましょう.

import numpy as np
import pandas as pd

import statsmodels
from statsmodels.tsa.stattools import coint
# just set the seed for the random number generator
np.random.seed(107)

import matplotlib.pyplot as plt

Pythonで非常に有名なチャートライブラリです. このチャートライブラリでは,

仮設の投資目標 X を生成し,通常の分布で日々の収益をシミュレートしてプロットします. その後,日々の X 値を得るための累積和を行います.

# Generate daily returns
Xreturns = np.random.normal(0, 1, 100) 
# sum them and shift all the prices up
X = pd.Series(np.cumsum(
    Xreturns), name='X') 
    + 50
X.plot(figsize=(15,7))
plt.show()

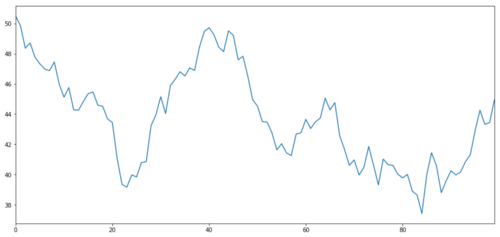
投資対象物のXは,通常の分布によって日々の収益を図示するためにシミュレーションされます.

Xの変化に非常に似ています. これをモデル化するには,Xを取って,それを上に移動し,通常の分布から抽出したランダムなノイズを加えます.

noise = np.random.normal(0, 1, 100)
Y = X + 5 + noise
Y.name = 'Y'
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.show()

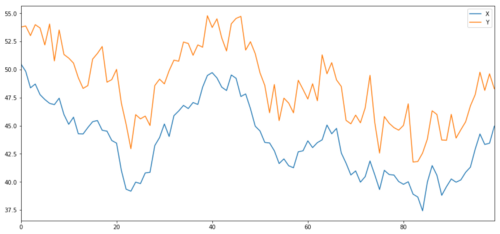
共同統合投資対象のXとY

統合

同積分は相関と非常に似ています.つまり,2つのデータシリーズ間の比率は平均値に近い変化をします.YとXシリーズは以下の通りです.

Y = X + e

は常数で eはノイズです

2つの時間列間の取引のペアでは,時間の経過とともに比率の期待値が平均値に収束しなければならない.つまり,それらは共同統合されるべきである.上記で構築した時間列は共同統合されている.現在,それらの間の比率をグラフ化して,それがどのように見えるかを見ることができます.

(Y/X).plot(figsize=(15,7)) 
plt.axhline((Y/X).mean(), color='red', linestyle='--') 
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()

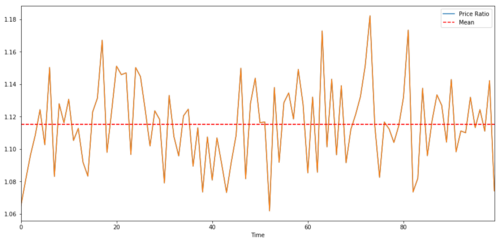
2つの共同投資目標価格の比率と平均値

共同統合試験

簡単なテスト方法として, statsmodels.tsa.stattools を使います. p値は非常に低く,可能な限り統合された2つのデータシリーズを人工的に作成しました.

# compute the p-value of the cointegration test
# will inform us as to whether the ratio between the 2 timeseries is stationary
# around its mean
score, pvalue, _ = coint(X,Y)
print pvalue

結果は1.81864477307e-17

注:相関と共同統合

関連性と共積分は,理論的には似ていますが,同じではありません. 関連性のある但し共積分されていないデータシリーズの例を見てみましょう. そしてその逆です. まず,私たちが生成したシリーズの関連性を確認しましょう.

X.corr(Y)

結果は: 0.951

2つの関連系はどうでしょうか? 単純な例は 2つの偏差データ系です.

ret1 = np.random.normal(1, 1, 100)
ret2 = np.random.normal(2, 1, 100)

s1 = pd.Series( np.cumsum(ret1), name='X')
s2 = pd.Series( np.cumsum(ret2), name='Y')

pd.concat([s1, s2], axis=1 ).plot(figsize=(15,7))
plt.show()
print 'Correlation: ' + str(X_diverging.corr(Y_diverging))
score, pvalue, _ = coint(X_diverging,Y_diverging)
print 'Cointegration test p-value: ' + str(pvalue)

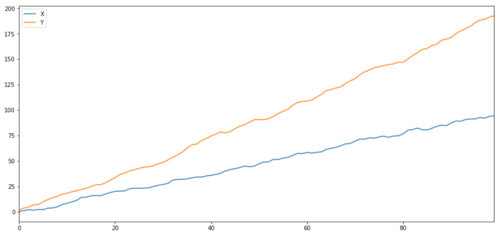
2つの関連シリーズ (統合されていない)

関連系数: 0.998 共同統合試験のP値: 0.258

関連性のない共積分の単純な例は,正規分布配列と平方波である.

Y2 = pd.Series(np.random.normal(0, 1, 800), name='Y2') + 20
Y3 = Y2.copy()
Y3[0:100] = 30

Y3[100:200] = 10
Y3[200:300] = 30
Y3[300:400] = 10
Y3[400:500] = 30
Y3[500:600] = 10
Y3[600:700] = 30
Y3[700:800] = 10
Y2.plot(figsize=(15,7))
Y3.plot()
plt.ylim([0, 40])
plt.show()
# correlation is nearly zero
print 'Correlation: ' + str(Y2.corr(Y3))
score, pvalue, _ = coint(Y2,Y3)
print 'Cointegration test p-value: ' + str(pvalue)

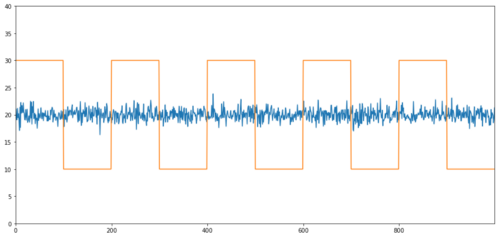
関連性:0.007546 共同統合試験のP値: 0.0

このp値は完璧な共積分を示しています

パア取引をどのように行うか?

2つの共同統合された時間列 (上記のXとYなど) が互いに向き合い,互いに逸脱しているため,時にはベース・スプレッドが高くまたは低くなります.我々は1つの投資対象物を購入し,もう1つを販売することによってペア取引を行います.この方法で,2つの投資目標が一緒に落ちたり上昇したりした場合,私たちはお金も得たり損したりしません.つまり,私たちは市場で中立です.

上記に戻り,Y= X+e の X と Y は,比率 (Y/X) が平均値の周りを移動するようにします.平均値逆転比率を通じてお金を稼ぎます.これを行うために,X と Y が遠く離れている場合,つまり の値が高くすぎるか低くすぎるかについて注意します.

• 長い比率:この比率が非常に小さいとき,増加することを期待します.上記の例では,Yを長くしてXを短くしてポジションを開きます.

• ショートレート (short ratio): ショートレート () が非常に大きく,減少すると予想されます.上記の例では,YをショートレートしてXをショートレートしてポジションを開きます.

取引対象が損失値で購入すると,ショートポジションは利益を得ます.また逆もです.したがって,私たちは市場全体の動向に免疫があります.

取引対象のXとYが 互いに相対的に動くと 利益を得たり損をするのです

類似した動作を持つ取引オブジェクトを見つけるためにデータを使用します

最良の方法は,取引対象から始め,共同統合を疑い,統計的なテストを行うことです.すべての取引対に対して統計的なテストを行うと,多重比較バイアス.

多重比較バイアス多くのテストを実行するときに重要なp値が誤って生成される可能性が増加することを指します.多くのテストを実行する必要があるからです. 100回のテストをランダムデータで実行すると,0.05未満の5p値を表示する必要があります. n (n-1) /2の比較を行う場合は,n (n-1) /2の比較を行います.多くの誤ったp値を表示します.これはテストサンプルの増加とともに増加します.この状況を避けるために,いくつかの取引ペアを選択し,それらの組み合わせが可能であることを決定する理由があり,それらを個別にテストします.これは大幅に減少します.多重比較バイアス.

S&P500指数に含まれる米国の大手技術株のバスケットを例に挙げましょう.これらの取引ターゲットは,類似した市場セグメントで動作し,共同統合価格を持っています.取引対象リストをスキャンし,すべてのペアの間の共同統合をテストします.

返された共積分テストスコアマトリックス,p値マトリックス,p値が0.05未満のすべてのペアこの方法は複数の比較偏見に 傾向があるので 実際には 2度目の検証が必要ですこの記事では,説明の便利さのために,この例のポイントを無視することを選択します.

def find_cointegrated_pairs(data):
    n = data.shape[1]
    score_matrix = np.zeros((n, n))
    pvalue_matrix = np.ones((n, n))
    keys = data.keys()
    pairs = []
    for i in range(n):
        for j in range(i+1, n):
            S1 = data[keys[i]]
            S2 = data[keys[j]]
            result = coint(S1, S2)
            score = result[0]
            pvalue = result[1]
            score_matrix[i, j] = score
            pvalue_matrix[i, j] = pvalue
            if pvalue < 0.02:
                pairs.append((keys[i], keys[j]))
    return score_matrix, pvalue_matrix, pairs

注:我々はデータに市場ベンチマーク (SPX) を含めており,市場は多くの取引対象の流れを動かす.通常,コインテグレートされているように見える2つの取引対象を見つけることができます.しかし,実際には,それらは互いにコインテグレートしません.これは混同変数と呼ばれます.あなたが見つけ出すいかなる関係においても市場参加を確認することが重要です.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2007/12/01'
endDateStr = '2017/12/01'
cachedFolderName = 'yahooData/'
dataSetId = 'testPairsTrading'
instrumentIds = ['SPY','AAPL','ADBE','SYMC','EBAY','MSFT','QCOM',
                 'HPQ','JNPR','AMD','IBM']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
data = ds.getBookDataByFeature()['Adj Close']
data.head(3)

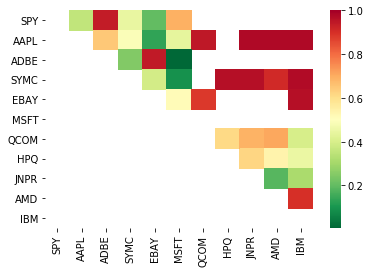
組み合わせた取引ペアを見つける方法を使ってみましょう. 組み合わせた取引ペアを見つける方法を使って,

# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds, 
                yticklabels=instrumentIds, cmap=’RdYlGn_r’, 
                mask = (pvalues >= 0.98))
plt.show()
print pairs

[('ADBE', 'MSFT')]

ADBEとMSFTが統合されているようです. 価格を見て,それが本当に意味があるか確認しましょう.

S1 = data['ADBE']
S2 = data['MSFT']
score, pvalue, _ = coint(S1, S2)
print(pvalue)
ratios = S1 / S2
ratios.plot()
plt.axhline(ratios.mean())
plt.legend([' Ratio'])
plt.show()

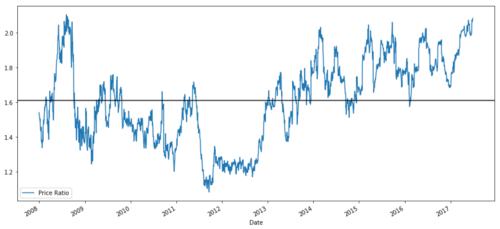
MSFTとADBEの価格比率グラフ (2008年から2017年)

この比率は安定した平均値に見えます.絶対比率は統計的に有用ではありません. Zスコアとして処理することでシグナルを標準化することがより役立ちます. Zスコアは以下のように定義されます:

Zスコア (値) = (値 平均値) /標準偏差

警告

実際,私たちは通常,データが正常分布であるという前提でデータを拡大しようとします. しかし,多くの金融データは正常分布ではありません. ですから,統計を作成するときに,単に正常性や特定の分布を想定しないように非常に注意する必要があります. 割合の真の分布は,脂肪尾効果を持ち,極端な傾向にあるデータは,私たちのモデルを混乱させ,大きな損失をもたらす可能性があります.

def zscore(series):
    return (series - series.mean()) / np.std(series)

zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()

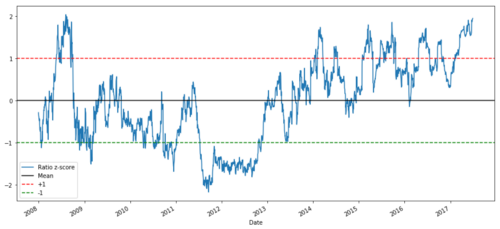
2008年から2017年のMSFTとADBEの価格比Z

平均値に近い比率の動きを観察するのは簡単ですが,時には平均値から大きな差があることも簡単です.

現在,ペア取引戦略の基礎知識について議論し,歴史的な価格に基づいて共同統合の主題を決定したので,取引信号を開発してみましょう.まず,データ技術を使用して取引信号の開発のステップをレビューしましょう.

• 信頼性の高いデータを収集し,データを整理する.

• 取引シグナル/論理を識別するためのデータから関数を作成する.

• 機能は移動平均値や価格データ,より複雑な信号の相関または比率であり,それらを組み合わせて新しい関数を作成できます.

• これらの機能を使って,取引信号を生成します. つまり,どの信号が買い,売,ショートポジションなのかを監視します.

FMZ Quant プラットフォーム (fmz.com戦略開発者にとって大きな恩恵です.私たちは,戦略論理の設計と機能の拡張にエネルギーと時間を費やすことができます.

FMZ Quant プラットフォームには,様々な主流の交換用のカプセル化されたインターフェースがあります.私たちがすべきことは,これらの API インターフェースを呼び出すことです.残りの基礎的な実装ロジックは,プロチームによって完成されています.

この記事で論理を完了し,原理を説明するために,これらの基礎論理を詳細に提示します.しかし,実際の操作では,読者は上記の4つの側面を完了するためにFMZ Quant APIインターフェースを直接呼び出すことができます.

始めよう

ステップ 1: 質問 を 立て

次の瞬間に買ったり売ったりするかどうかを示す信号を作成します つまり予測変数Yです

Y = 割引は,買 (1) か売 (-1)

Y (t) =サイン (t) 比 (t+1) 比 (t)

実際の取引目標価格や,比率の実際の値さえ予測する必要がないことに注意してください (できるが),次のステップでは比率の方向のみです.

ステップ2: 信頼性と正確さのあるデータ収集

FMZ Quantはあなたの友人です! 取引対象とデータソースを指定するだけで,必要なデータを抽出し,配当と取引対象分割のためにクリアします. ここでデータは非常にきれいです.

過去10年間の取引日 (約2500データポイント) のYahoo Financeを用いて以下のデータを得ました. 開始価格,閉値,最高価格,最低価格,取引量.

ステップ3:データを分割する

モデルの正確性をテストする際のこの非常に重要なステップを忘れないでください.我々は,訓練/検証/テストの分割のために以下のデータを使用しています.

• 訓練7年~70%

• 試験~3年 30%

ratios = data['ADBE'] / data['MSFT']
print(len(ratios))
train = ratios[:1762]
test = ratios[1762:]

理想的には 検証セットも作るべきですが 今のところはしません

ステップ4 機能工学

関連関数はどのようなものになるのでしょうか?比率変化の方向性を予測したいです.我々の2つの取引目標が統合されていることを見ました.したがってこの比率は平均値に移動し戻る傾向があります.我々の特徴は平均比率のいくつかの尺度であり,現在の値と平均値の差が我々の取引信号を生成できるようです.

次の関数を使用します.

• 60日間の移動平均比:ローリング平均の測定

• 5日間の移動平均比:平均の現在の値の測定

• 60日標準偏差

• Zスコア: (5d MA - 60d MA) / 60d SD

ratios_mavg5 = train.rolling(window=5,
                               center=False).mean()
ratios_mavg60 = train.rolling(window=60,
                               center=False).mean()
std_60 = train.rolling(window=60,
                        center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()

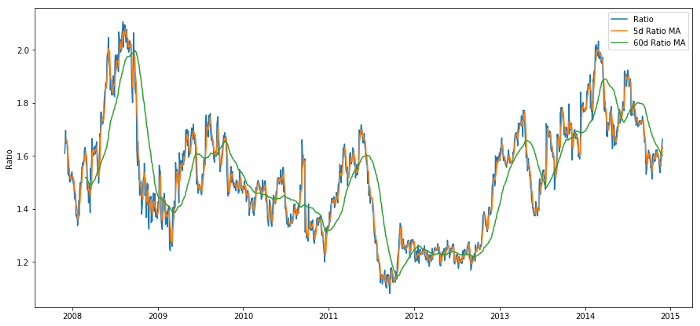
価格比60dから5dMA

plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()

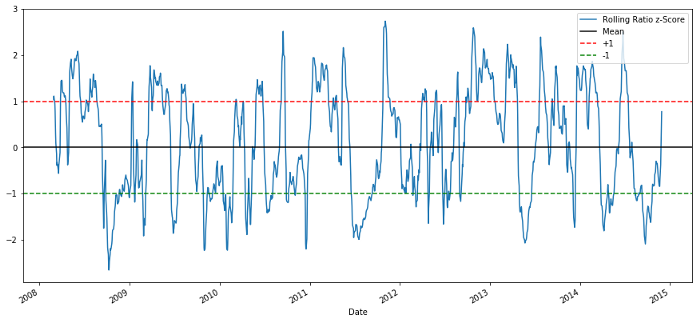
60-5 Zスコア価格比率

平均値のZスコアは 平均値回帰特性を示しています

ステップ 5: モデルの選択

簡単なモデルから始めましょう. zスコアグラフを見ると, zスコアが高くすぎるか低くすぎるか,戻ってくるのがわかります. 高いと低いを定義するために+1/- 1を限界値として使用します.

• zが0に戻ると予想されるので,比率が増加します.

• zが0に返ると,比率が減ります. この比率が0に返ると,

ステップ 6:訓練,検証,最適化

この信号が実際の比率に対するパフォーマンスを見てみましょう.

# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color=’g’, linestyle=’None’, marker=’^’)
sell[60:].plot(color=’r’, linestyle=’None’, marker=’^’)
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend([‘Ratio’, ‘Buy Signal’, ‘Sell Signal’])
plt.show()

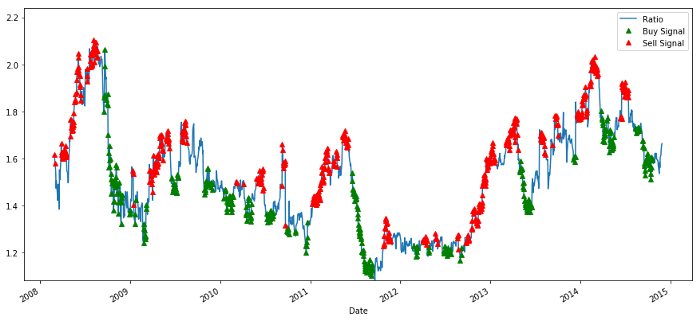
購入・販売価格比の信号

信号は合理的に見える. 値が高くなったり上昇したときに (赤い点) 売って,値が低くなったり下がったときに (緑色の点) 買い戻すように見える. これは取引の実際の対象に何を意味するのか? 見てみよう:

# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1 = data['ADBE'].iloc[:1762]
S2 = data['MSFT'].iloc[:1762]
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2 
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['ADBE','MSFT', 'Buy Signal', 'Sell Signal'])
plt.show()

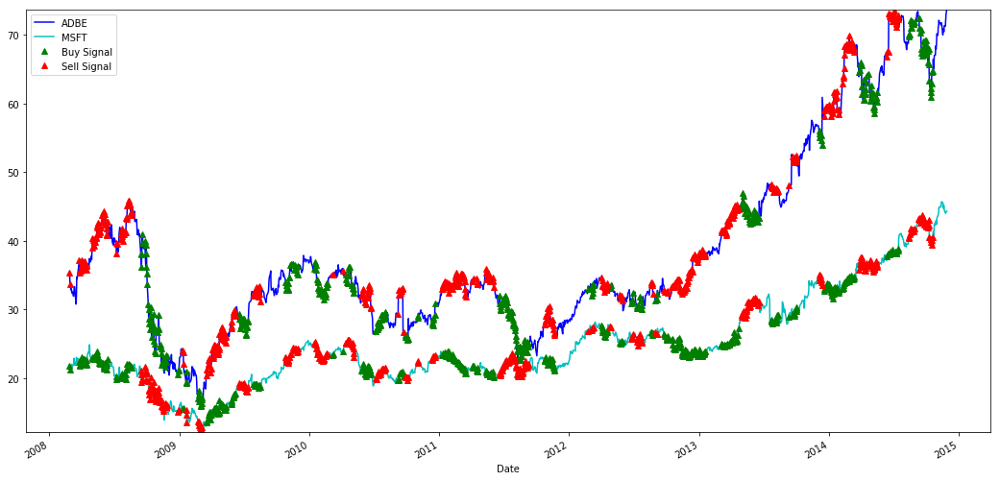
MSFTとADBEの株式の購入・売却のシグナル

短足で利益を得たり 長い足で利益を得たり 両方をすることもあります

訓練データの信号に満足しています. この信号がどのような利益を生むか見てみましょう. 比率が低いとき,簡単なバックテストを行い,比率 (1 ADBE株を買って比率x MSFT株を売って比率) を購入し,比率 (1 ADBE株を売って比率x MSFT株を買って比率) を高くなると販売し,これらの比率の PnL取引を計算できます.

# Trade using a simple strategy
def trade(S1, S2, window1, window2):
    
    # If window length is 0, algorithm doesn't make sense, so exit
    if (window1 == 0) or (window2 == 0):
        return 0
    
    # Compute rolling mean and rolling standard deviation
    ratios = S1/S2
    ma1 = ratios.rolling(window=window1,
                               center=False).mean()
    ma2 = ratios.rolling(window=window2,
                               center=False).mean()
    std = ratios.rolling(window=window2,
                        center=False).std()
    zscore = (ma1 - ma2)/std
    
    # Simulate trading
    # Start with no money and no positions
    money = 0
    countS1 = 0
    countS2 = 0
    for i in range(len(ratios)):
        # Sell short if the z-score is > 1
        if zscore[i] > 1:
            money += S1[i] - S2[i] * ratios[i]
            countS1 -= 1
            countS2 += ratios[i]
            print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
        # Buy long if the z-score is < 1
        elif zscore[i] < -1:
            money -= S1[i] - S2[i] * ratios[i]
            countS1 += 1
            countS2 -= ratios[i]
            print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
        # Clear positions if the z-score between -.5 and .5
        elif abs(zscore[i]) < 0.75:
            money += S1[i] * countS1 + S2[i] * countS2
            countS1 = 0
            countS2 = 0
            print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
            
            
    return money
trade(data['ADBE'].iloc[:1763], data['MSFT'].iloc[:1763], 60, 5)

結果は 1783.375 です

移動平均の時間窓を変更して, 買い/売りと閉じるポジションの値を変更して, 検証データのパフォーマンス改善をチェックすることで,さらに最適化することができます.

1/−1を予測するために ロジスティック回帰やSVMなど より複雑なモデルも試すことができます

このモデルを進めてみましょう.

ステップ7 テストデータをバックテストする

ここでまた,FMZ Quantプラットフォームは,歴史的な環境を真に再現し,一般的な定量バックテストの落とし穴をなくし,リアルボット投資をより良く助けるために,戦略の欠陥を時間内に発見するために,高性能QPS/TPSバックテストエンジンを採用しています.

原則を説明するために,この記事は依然として基礎的な論理を示すことを選択しています.実用的な応用では,読者がFMZ Quantプラットフォームを使用することをお勧めします.時間を節約するだけでなく,エラー寛容率を改善することが重要です.

テストデータの PnL を表示するために上記の関数を使用できます.

trade(data['ADBE'].iloc[1762:], data['MSFT'].iloc[1762:], 60, 5)

結果は,5262,868でした

モデルがうまくいきました 最初のシンプルなペア取引モデルになりました

オーバーフィッティングを避ける

議論を締めくくる前に,特にオーバーフィッティングについてお話ししたいと思います.オーバーフィッティングは取引戦略における最も危険な罠です.オーバーフィッティングアルゴリズムはバックテストで非常にうまく機能しますが,新しい目に見えないデータでは失敗します.これは,データのトレンドを明らかにせず,実際の予測能力がないことを意味します.簡単な例を挙げましょう.

モデルでは,時間窓の長さを推定し最適化するためにローリングパラメータを使用します.すべての可能性,合理的な時間窓の長さを繰り返して,モデルの最高のパフォーマンスに応じて時間の長さを選択することを決定することができます.訓練データの pnl に基づいて時間窓の長さをスコアするために簡単なループを書いて,最高のループを見つけましょう.

# Find the window length 0-254 
# that gives the highest returns using this strategy
length_scores = [trade(data['ADBE'].iloc[:1762], 
                data['MSFT'].iloc[:1762], l, 5) 
                for l in range(255)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)

('Best window length:', 40)

テストデータに対するモデルのパフォーマンスを調べてみると この時間窓の長さは最適とは程遠いことがわかりました なぜなら 当初の選択が 明らかにサンプルデータに 過剰に適合していたからです

# Find the returns for test data
# using what we think is the best window length
length_scores2 = [trade(data['ADBE'].iloc[1762:], 
                  data['MSFT'].iloc[1762:],l,5) 
                  for l in range(255)]
print (best_length, 'day window:', length_scores2[best_length])
# Find the best window length based on this dataset, 
# and the returns using this window length
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])

(40, 'day window:', 1252233.1395)
(15, 'day window:', 1449116.4522)

試験のために,この2つのデータセットから計算された長さのスコアをグラフ化してみましょう.

plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()

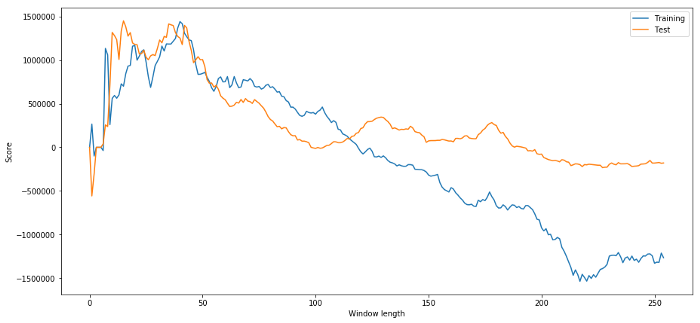
20〜50の物件は タイムウィンドウに適しています

オーバーフィッティングを避けるために,時間窓の長さを選択するために経済推論またはアルゴリズムの性質を使用することができます.また,長さを指定する必要のないカルマンフィルターを使用できます.このアプローチは,別の記事で後で説明します.

次のステップ

この記事では,取引戦略の開発プロセスを示すための簡単な導入方法を提案します.実際は,より複雑な統計を使用する必要があります.以下のオプションを検討することができます:

• ハースト指数

• オーンシュタイン・ウレンベックプロセスから推測された平均回帰半減期

• カルマンフィルター

関連性

もっと