プログラムトレーダーのための強力なツール: 平均値と変数を計算するための漸進的な更新アルゴリズム

紹介

プログラム式取引では,移動平均値や変動指標などの平均値と変動値を計算することがしばしば必要である.高周波および長期計算が必要な場合,歴史的なデータを長期間にわたって保持することが必要であり,それは不要であり資源を消費する.この記事は,重度の平均値と変動値を計算するためのオンライン更新アルゴリズムを紹介している.これはリアルタイムデータストリームを処理し,特に高周波戦略を動的に調整するために特に重要です.この記事では,トレーダーがアルゴリズムを迅速に展開し,実際の取引に適用するのに役立つ対応する Python コード実装も提供しています.

単純な平均と変数

薬剤を服用すると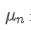n番目のデータポイントの平均値を表示するために,n-1データポイント /upload/asset/28e28ae0beba5e8a810a6.pngの平均を既に計算したと仮定し,新しいデータポイント /upload/asset/28d4723cf4cab1cf78f50.pngを受け取ります.新しい平均数を計算したいです.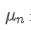新しいデータポイントを含む. 以下は詳細な導出です.

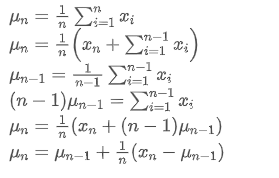
バランス更新プロセスは次のステップに分けられる:

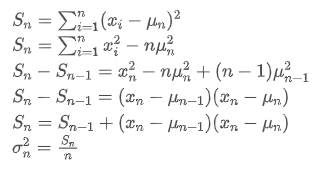
このプロセスは,新しいデータポイントを受け取るたびに新しい平均値と偏差値を更新することを可能にします.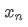過去のデータの平均値と変数を保存せずに,以前のデータの平均値と変数を保持することで,計算をより効率化します.しかし,問題は,この方法で計算するものはすべてのサンプルの平均値と変数であり,実際の戦略では,一定の固定期間を考慮する必要があります.上記の平均値更新を観察すると,新しい平均値更新の量は,新しいデータと過去の平均値との間の偏差を比率で掛けます.この比率が固定された場合,それは指数的に重量化された平均値につながります.次に議論します.

指数関数で重んじられた平均値

指数的な重み平均は,次の再帰関係によって定義できる.

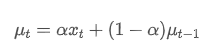
その中には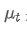時間点 t の指数的な重み平均値です.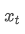観測値 t,α は重量因数,そして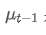前回の時間点の指数的な重み平均です.

指数関数で重んじられた変数

変数については,各時間点における偏差の平方偏差の指数的な重み平均を計算する必要があります.これは次の再帰関係によって達成できます.

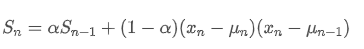
その中には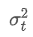時間点 t の指数関数重度の偏差であり,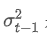前回の時間点の指数関数重量変数です.

指数関数重度の平均値と分散値を観察する.それらの漸進的な更新は直感的に,過去の値の一部を保持し,新しい変化を追加する.この論文では,特定の派生プロセスを参照することができます:https://fanf2.user.srcf.net/hermes/doc/antiforgery/stats.pdf

SMAとEMA

SMA (算術平均値としても知られる) と EMAは,それぞれ異なる特徴と用途を持つ2つの一般的な統計指標である.前者は,データセットの中央位置を反映して,各観測に等しい重みを割り当てます.後者は,より最近の観測により高い重みを与える再帰計算方法です.現在時間からの距離が各観測に増加するにつれて重量は指数的に減少します.

• 体重分布: SMAは各データポイントに同じ重みを割り当て,EMAは最新のデータポイントにより高い重みを付けます.
• 新しい情報に対する敏感性:SMAは,すべてのデータポイントを再計算することを伴うため,新たに追加されたデータに対して十分に敏感ではありません.一方,EMAは,最新のデータの変化をより迅速に反映することができます.
• 計算の複雑性: SMAの計算は比較的簡単ですが,データポイントの数が増えるにつれて計算コストも増加します. EMAの計算はより複雑ですが,再帰性性があるため,連続したデータストリームをより効率的に処理できます.

EMA と SMA の間での推定変換方法

SMAとEMAは概念的に異なるが,適切なα値を選択することで,EMAを特定の観測数を含むSMAに近似させることができる.この近似関係は,EMAの重量因子αの関数である有効サンプルサイズによって記述することができる.

SMAは,与えられた時間窓内のすべての価格の算術平均値である.時間窓 N に対して,SMAの中点 (すなわち平均数が位置する位置) は以下のように考えることができる:

SMA の 中心体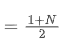

EMAは,最も最近のデータポイントがより大きな重量を持つ重量平均の一種である. EMAの重量は時間とともに指数関数的に減少する. EMAの中点は,次の連続を要約することによって得ることができる:

EMA の 中心部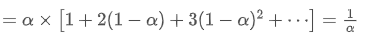

SMA と EMA が同じ中点体を持っていると仮定すると,

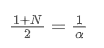
この方程式を解くには α と N の関係を得ることができます

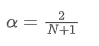
これは,N日間の与えられたSMAに対して,対応するα値は,同等なEMAを計算するために使用でき,同じ中点があり,結果は非常に類似していることを意味します.

異なる更新頻度を持つ EMA の変換

これは,毎秒,新しいデータポイントが EMA に追加され/upload/asset/28da19ef219cae323a32f.png の重みで,古いデータポイントの影響は /upload/asset/28cfb008ac438a12e1127.png で掛けられます.

f秒ごとに更新するなど更新頻度を変更すると,新しい重量因子 /upload/asset/28d2d28762e349a03c531.png を求めます.

f秒以内に,更新が行われなければ,古いデータポイントの影響は,毎回 /upload/asset/28e50eb9c37d5626d6691.png に掛ける f倍に連続的に衰える.したがって,f秒後の総衰退因子は /upload/asset/28e296f97d8c8344a2ee6.png である.

f秒ごとに更新される EMA が 1 更新期内の 1 秒ごとに更新される EMA と同じ衰退効果を持つようにするには, f秒後の総衰退因子を 1 更新期内の衰退因子に等しくします.

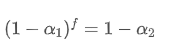
この方程式を解くと,新しい重量因子を得ます.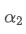

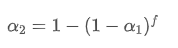
この式は,更新頻度が変わるときに EMA の平滑効果が変化しない新しい重量因子 /upload/asset/28d2d28762e349a03c531.png の近似値を提供します.例えば:平均価格を計算するとき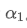値が0.001で,10秒ごとに更新し,毎秒更新に変更される場合,相当値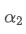値が 0.01 になります.

Python コードの実装

class ExponentialWeightedStats:
    def __init__(self, alpha):
        self.alpha = alpha
        self.mu = 0
        self.S = 0
        self.initialized = False

    def update(self, x):
        if not self.initialized:
            self.mu = x
            self.S = 0
            self.initialized = True
        else:
            temp = x - self.mu
            new_mu = self.mu + self.alpha * temp
            self.S = self.alpha * self.S + (1 - self.alpha) * temp * (x - self.mu)
            self.mu = new_mu

    @property
    def mean(self):
        return self.mu

    @property
    def variance(self):
        return self.S

# Usage example
alpha = 0.05  # Weight factor
stats = ExponentialWeightedStats(alpha)
data_stream = [] # Data stream
for data_point in data_stream:
    stats.update(data_point)

概要

高周波プログラミング取引では,リアルタイムデータの迅速な処理が不可欠である.計算効率を向上させ,資源消費を削減するために,この記事はデータストリームの重度の平均値と変数を継続的に計算するためのオンライン更新アルゴリズムを導入する.リアルタイムインクリメンタル更新は,大きな可能性を持つ2つの資産価格間の相関,線形フィットメントなど,さまざまな統計データおよび指標計算のためにも使用できる.インクリメンタル更新はデータを信号システムとして扱っており,これは固定期間の計算と比較して思考の進化である.あなたの戦略にはまだ歴史的なデータを使用して計算する部分が含まれている場合,このアプローチに従って変換することを検討してください:新しいデータが到着するときにシステム状態の推定を記録し,システム状態を更新するのみ;このサイクルを繰り返します.