ベイズ - 確率を解読する秘訣 意思決定の背後にある数学的な知恵を探求

ベイエス統計学は,数学分野における強力な大学科であり,金融,医学研究,情報技術を含む多くの分野に広く応用されている.それは,以前の信念と証拠を組み合わせ,新しい後遺的信念を導き,より賢明な意思決定を行うことを可能にします.

この記事では,この分野を創立した主要な数学者について簡単に説明します.

バイエスより前に ベイエスの統計学をよりよく理解するには,18世紀に戻り,数学者デ・モイヴレとその論文"確率の原理"を参考にする必要がある[1].

彼の論文では,デ・モイヴレは彼の時代における確率とギャンブルに関する多くの問題を解決した. 恐らくご存知のように,その問題の1つに対する彼の解決策は正規分布の起源につながったが,それは別の話である.

論文の中で最も簡単な質問があります.

公平なコインを3回連続で投げると,3つの正の確率が得られる.

確率の原理欄で説明されている問題を読むと,それらの問題のほとんどは仮定から始まり,そこから与えられた出来事の確率を計算することに気付くかもしれません.例えば,上記の問題では,コインが公平であると考えられる仮定があり,したがって投じられた場合の正の確率は0.5である.

現代の数学用語では,

𝑃(𝑋|𝜃)

しかし,もしこのコインが公平か否か分からないとしたら?𝜃ほら

トーマス・ベイズとリチャード・プレイス

およそ50年後,1763年に,の解決の原則に関する問題に関する論文が[2]に掲載され,ロンドン・ロイヤル・ソસાયティの哲学取引のに掲載された.

文書の最初の数ページには,数学者リチャード・プライスが彼の友であるトーマス・ベイズの死前数年の論文を要約した文章がある.この紹介文では,プライスは,トーマス・ベイズのいくつかの発見の重要性を説明し,これらの発見は,デ・モイヴレのの確率原理に含まれていない.

この記事へのトラックバック一覧です.

は,既知の未知イベントの発生と失敗回数を,その発生の確率を,任意の2つの命名された確率度間の確率値で探す.

つまり,未知のパラメータを観測した結果,θ2つの確率度間の確率は何である. これは実際に歴史上最初の統計推論に関する問題の一つであり,逆確率という名前をもたらした. 数学用語では:

𝑃( 𝜃 | 𝑋）

これはもちろん,今日私たちがベイエスの定理と呼んでいる 後後の分布である.

原因不明

この2人の長老を知り,トーマス・ベイエスそしてリチャード・プレイスしかし,それを行うには,一時的に統計学の知識を置く必要があります.

18世紀には,確率が数学者にとってますます関心のある分野になっている.デモファーやベルヌーリのような数学者たちは,ある種の出来事が一定の確率で起こるが,それでも固定されたルールによって支配されていることを示している.例えば,もしあなたが何度もデッキを投げたら,6分の1の時間が6で止まる.それは,隠されたルールがチャンスの運命を決定しているようなものだ.

この時代を生きていた数学者で敬虔な信徒だと想像してみてください. この隠れた法則と神の関係について知りたくなるかもしれません.

これは確かにバイズとプライスが自問した問題である.彼らは,この問題の解決法を直接的に適用して,の世界が,知性と知性の結果である必要があることを証明することを望んだ.したがって,最終的な原因で神の存在を証明する[2] - つまり,無因果的な原因 - を提供した.

ラプラス

驚くことに,約2年後の1774年,明らかにトーマス・ベイエスの論文を読んでいなかったフランスの数学者ラプラスは,事件の確率によって事件の原因をくという論文を書いた[3].これは逆確率問題に関する論文である.最初のページでは,

基本的な原則は:

事件が n つの異なる原因によって引き起こされる場合,与えられた事件のこれらの原因の確率の相互比は,与えられた原因の出来事の確率に等しく,これらの原因のそれぞれが存在する確率は,与えられた事件の原因の確率に等しく,これらの原因のそれぞれが起こる確率の合計を除いて,与えられた事件の原因の確率に等しくなる.

これは,今日私たちが知っているベイエスの定理です.

​

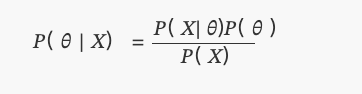
その中でもP(θ)均等に分布している.

コイン実験

PythonとPyMCのライブラリを使って,ベイエスの統計を現在まで持ってきて,簡単な実験を行います.

友人があなたにコインをあげて,それが公平だと思うか尋ねるとしましょう. 彼は急いでいて,あなたにコインを10回しか投げることができないと言いました.p確率を計算します. 確率を計算してみましょう.p可能性が高い値です.

(注:これはパラメータではありません)pランダムな変数ではなく,このパラメータが固定されているので,どの値の間に最も可能性が高いのか知りたいです.

この問題について異なる見解を持つために,私たちは二つの異なる先入観に基づいて解決します.

• 1 通貨の公平性についての事前の知識がない場合,pこの場合は,無情報先例と呼ばれるものを使用します. なぜなら,あなたはあなたの信念に何も追加していないからです.

• 2 あなたは経験から知っています.コインが不公平であっても,それを非常に不公平にするのは困難です.p0.3以下または0.7以上ではない可能性が高い.この場合は,情報先端を使用します.

この2つの状況において,我々の先入観は以下のとおりである.

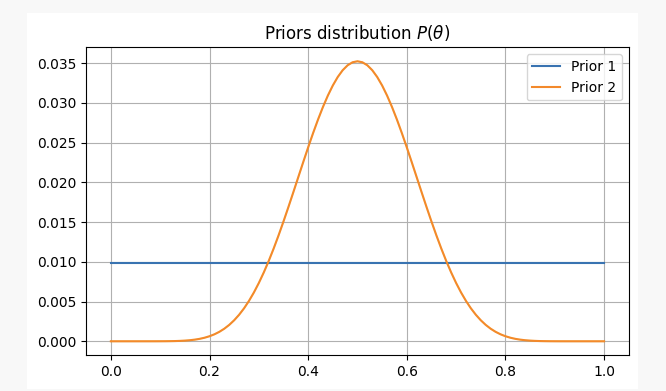
この証拠があれば,私たちはおそらく,私たちの参数を見つける場所です. そして,この式は,この式を,この式を,この式を,この式を,この式を,この式を,この式を,この式を,この式を,この式を,この式を,この式を,この式を,この式を,この式を,この式を,この式を,この式を,この式を,この式を,この式を.p？

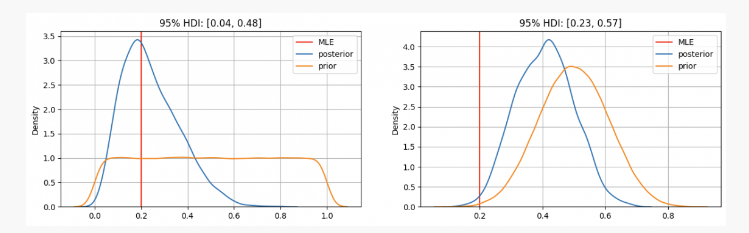
参数について考えます. 参数について考えます.pMLEは,最も似通りの推定値 (MLE) に集中している.p=0.2,これは周波数学問方法を用いたような方法である. 真の未知参数は95%信頼区間,0.04から0.48の間に位置する.

高い信頼度で,このパラメータはp0.3 と 0.7 の間にある場合,我々は,MLE で与えられた値よりもはるかに高い 0.4 の周辺の後期分布を見ることができる.この場合,真の未知参数は 95% の信頼区間で,0.23 と 0.57 の間にあるだろう.

だから,最初のケースでは,あなたはあなたの友人に,あなたがこのコインが不公平だと確信していることを伝えます. しかし,別のケースでは,あなたは彼に,あなたがコインが公平かどうか確信できないことを伝えます.

ご覧の通り,同じ証拠がある場合でも,10回の投じのうち2回の投じが正である場合でも,異なる先入観信念の下で結果は異なる.これは,科学的な方法と同様に,先入観信念と新しい観察と証拠を組み合わせることで私たちの信念を更新することを可能にするベイエス統計学の利点である.

エンド

本日の記事では,ベアスの統計学の起源と主な貢献者について説明します.その後,この分野には他の重要な貢献者 (ジェフリーズ,コックス,シャノンなど) がたくさんいます.转载自quantdare.com。