永続的な契約格子戦略パラメータの最適化詳細

永続格子戦略はプラットフォームで非常に人気のある古典的な戦略である. 現金格子と比較してコインを保持しない,レバレッジを上げることができる,現金格子よりも便利である. しかし,発明者のプラットフォームで直接回測を量化することができないため,コインの種類をフィルタリングし,パラメータの最適化を決定することが不利であるため,この記事では,データ収集,回測フレームワーク回測,測定関数,パラメータの最適化などのあらゆる側面を含む完全なPython回測プロセスを紹介します. juypter notebookで自分で試してみることができます.

データ収集

一般にK線データで十分である.精度のために,K線周期が小さいほど良いが,リトレース時間とデータ量をバランスする.この記事では,過去2年間のデータをリトレースするために5minを使用し,最終的なデータ量は20W線を超えた.通貨はDYDXを選択する.もちろん,特定の通貨とK線周期は,自分の興味に応じて選択することができます.

import requests
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import requests, zipfile, io
%matplotlib inline

def GetKlines(symbol='BTC',start='2020-8-10',end='2021-8-10',period='1h'):
    Klines = []
    start_time = int(time.mktime(datetime.strptime(start, "%Y-%m-%d").timetuple()))*1000
    end_time = int(time.mktime(datetime.strptime(end, "%Y-%m-%d").timetuple()))*1000
    while start_time < end_time:
        res = requests.get('https://fapi.binance.com/fapi/v1/klines?symbol=%sUSDT&interval=%s&startTime=%s&limit=1000'%(symbol,period,start_time))
        res_list = res.json()
        Klines += res_list
        start_time = res_list[-1][0]
    return pd.DataFrame(Klines,columns=['time','open','high','low','close','amount','end_time','volume','count','buy_amount','buy_volume','null']).astype('float')

df = GetKlines(symbol='DYDX',start='2022-1-1',end='2023-12-7',period='5m')
df = df.drop_duplicates()

復習枠

復習は,これまでよく使用されていたUSDTをサポートする永続的な契約多通貨の枠組みを選択し続け,シンプルで便利である.

class Exchange:
    
    def __init__(self, trade_symbols, fee=0.0004, initial_balance=10000):
        self.initial_balance = initial_balance #初始的资产
        self.fee = fee
        self.trade_symbols = trade_symbols
        self.account = {'USDT':{'realised_profit':0, 'unrealised_profit':0, 'total':initial_balance, 'fee':0}}
        for symbol in trade_symbols:
            self.account[symbol] = {'amount':0, 'hold_price':0, 'value':0, 'price':0, 'realised_profit':0,'unrealised_profit':0,'fee':0}
            
    def Trade(self, symbol, direction, price, amount):
        
        cover_amount = 0 if direction*self.account[symbol]['amount'] >=0 else min(abs(self.account[symbol]['amount']), amount)
        open_amount = amount - cover_amount
        self.account['USDT']['realised_profit'] -= price*amount*self.fee #扣除手续费
        self.account['USDT']['fee'] += price*amount*self.fee
        self.account[symbol]['fee'] += price*amount*self.fee

        if cover_amount > 0: #先平仓
            self.account['USDT']['realised_profit'] += -direction*(price - self.account[symbol]['hold_price'])*cover_amount  #利润
            self.account[symbol]['realised_profit'] += -direction*(price - self.account[symbol]['hold_price'])*cover_amount
            
            self.account[symbol]['amount'] -= -direction*cover_amount
            self.account[symbol]['hold_price'] = 0 if self.account[symbol]['amount'] == 0 else self.account[symbol]['hold_price']
            
        if open_amount > 0:
            total_cost = self.account[symbol]['hold_price']*direction*self.account[symbol]['amount'] + price*open_amount
            total_amount = direction*self.account[symbol]['amount']+open_amount
            
            self.account[symbol]['hold_price'] = total_cost/total_amount
            self.account[symbol]['amount'] += direction*open_amount
                    
    
    def Buy(self, symbol, price, amount):
        self.Trade(symbol, 1, price, amount)
        
    def Sell(self, symbol, price, amount):
        self.Trade(symbol, -1, price, amount)
        
    def Update(self, close_price): #对资产进行更新
        self.account['USDT']['unrealised_profit'] = 0
        for symbol in self.trade_symbols:
            self.account[symbol]['unrealised_profit'] = (close_price[symbol] - self.account[symbol]['hold_price'])*self.account[symbol]['amount']
            self.account[symbol]['price'] = close_price[symbol]
            self.account[symbol]['value'] = abs(self.account[symbol]['amount'])*close_price[symbol]
            self.account['USDT']['unrealised_profit'] += self.account[symbol]['unrealised_profit']
        self.account['USDT']['total'] = round(self.account['USDT']['realised_profit'] + self.initial_balance + self.account['USDT']['unrealised_profit'],6)

格子回帰関数

格子戦略の原理はシンプルで,売り上げは上昇し,買い上げは下がり,具体的には3つのパラメータに関係している:初期価格,格子間隔,取引価値.DYDXの市場変動は非常に大きい.初期8.6Uの最低値から1Uを下回り,最近の牛市が3Uに戻った.戦略のデフォルトの初期価格は8.6Uで,これは格子戦略にとって非常に不利である.しかし,デフォルトパラメータは2年間の合計利益9200Uを回転させ,その間に7500Uを失っている.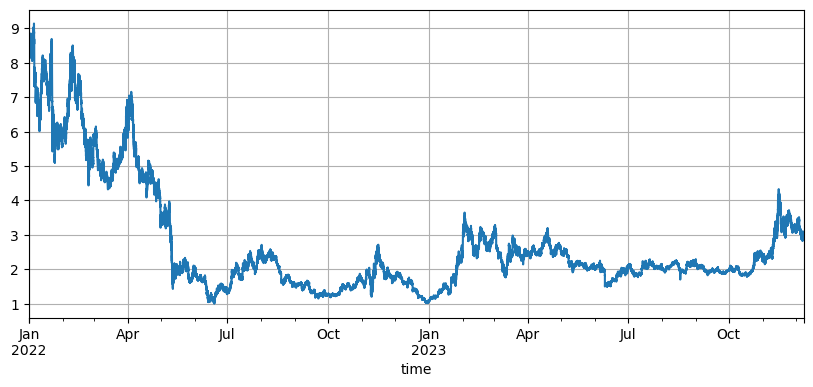

symbol = 'DYDX'
value = 100
pct = 0.01

def Grid(fee=0.0002, value=100, pct=0.01, init = df.close[0]):
    e = Exchange([symbol], fee=0.0002, initial_balance=10000)
    init_price = init
    res_list = [] #用于储存中间结果
    for row in df.iterrows():
        kline = row[1] #这样会测一根K线只会产生一个买单或一个卖单，不是特别精确
        buy_price = (value / pct - value) / ((value / pct) / init_price + e.account[symbol]['amount']) #买单价格，由于是挂单成交，也是最终的撮合价格
        sell_price = (value / pct + value) / ((value / pct) / init_price + e.account[symbol]['amount'])
        if kline.low < buy_price: #K线最低价低于当前挂单价，买单成交
            e.Buy(symbol,buy_price,value/buy_price)
        if kline.high > sell_price:
            e.Sell(symbol,sell_price,value/sell_price)
        e.Update({symbol:kline.close})
        res_list.append([kline.time, kline.close, e.account[symbol]['amount'], e.account['USDT']['total']-e.initial_balance,e.account['USDT']['fee'] ])
    res = pd.DataFrame(data=res_list, columns=['time','price','amount','profit', 'fee'])
    res.index = pd.to_datetime(res.time,unit='ms')
    return res

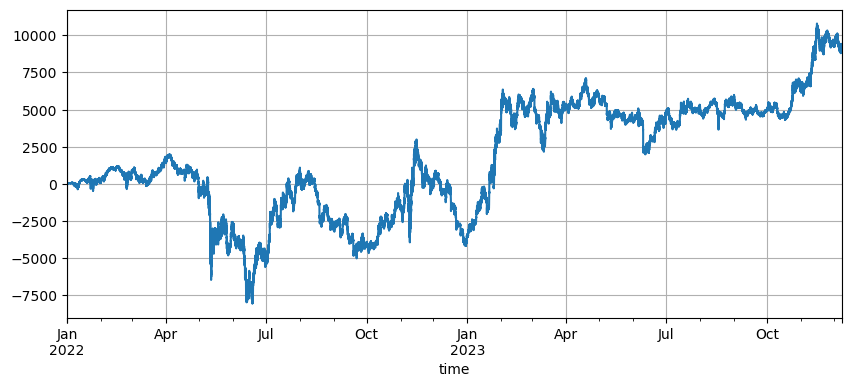
初期価格の影響

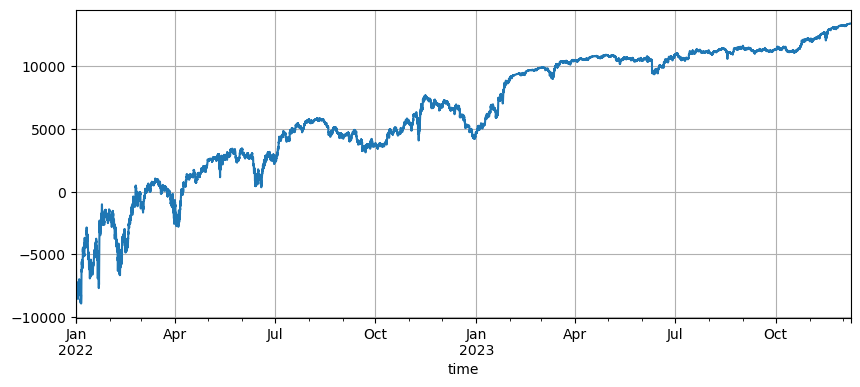
初期価格の設定は,戦略の初期持有に影響を与え,ちょうど再確認したデフォルト初期価格は,開始時の初期価格である. つまり,開始時に持たない. そして,格子戦略は,価格が開始時に戻るとすべての利益を稼ぐことを知っているので,戦略の開始時に将来の動きを正しく予測できれば,利回りが著しく向上します. ここで初期価格を3Uに設定し,再確認します. 最終的な最大引き上げは9200Uで,最終的な収益は13372Uです. 最終戦略は持たない. この利回りは,すべての変動利回りであり,デフォルトパラメータの利回りの差は,最終価格の判断に持参損失を許さないという部分です.

しかし,初期価格が3Uと設定され,戦略は初期から空き状態を大量に保持し,この例では直接1万7000Uの空き状態を保持し,それによりリスクが高い.

格子間隔設定

格子間隔は,挂字の距離を決定する.明らかに,格子間隔が小さいほど取引が頻繁になり,単筆の利益が低くなり,手続費も高くなる.しかし,格子間隔が小さくなり,格子価値は変化しないことに注意する.価格が変化すると,総保有量は増加し,リスクはまったく異なります.したがって,格子間隔の作用を再測するには,格子価値を計算する必要があります.

リトーストは5mK線データを使用し,K線で1回のみ取引されるため,これは明らかに不現実である.特にデジタル通貨の波動率は非常に大きく,リトーストでは実盤と比較して小さな間隔が多くの取引を逃す.このリトーストメカニズムでは,結論は正確ではない.ティックレベルのオーダーフローデータリトーストによって,最適な格子間隔は0.005-0.01であるべきである.

for p in [0.0005, 0.001 ,0.002 ,0.005, 0.01, 0.02, 0.05]:
    res = Grid( fee=0.0002, value=value*p/0.01, pct=p, init =3)
    print(p, round(min(res['profit']),0), round(res['profit'][-1],0), round(res['fee'][-1],0))
    
0.0005 -8378.0 144.0 237.0
0.001 -9323.0 1031.0 465.0
0.002 -9306.0 3606.0 738.0
0.005 -9267.0 9457.0 781.0
0.01 -9228.0 13375.0 550.0
0.02 -9183.0 15212.0 309.0
0.05 -9037.0 16263.0 131.0

ネットワーク取引の価値

前述したように,波動が同時にあるとき,保有価値が大きくなるほど,リスクなどの比率的方法が用いられるが,急激な減少でない限り,1%の総資本と1%の格子間隔は,ほとんどの市場に対応すべきである.この例では,DYDXでは,ほぼ90%の減少が爆破を誘発した.しかし,DYDXは主に下落であり,下落時には格子戦略を多く行う,最大でも100%を下落し,上昇は制限なしであり,リスクが高い.したがって,格子戦略は,ユーザが潜在的なコインを多く選ぶことを推奨する.

変形回帰価格

回帰価格とは,現在の価格と初期価格の差と格子の大きさが,どれくらいのポジションを保有すべきかを決定する.回帰価格が現在の価格よりも高く設定された場合,格子戦略は多くを行うが,逆に空になる.デフォルト回帰価格は,戦略の開始時の価格である.リスクを軽減するために,多くの格子だけを推奨する.自然な考えは,回帰価格を変えることができないことであり,価格が上昇したとしても,継続的に多くの格子を保持し,自動調整しないことである.BTCの今年の動向は,例えば,年初15000から年末43,000まで上昇する.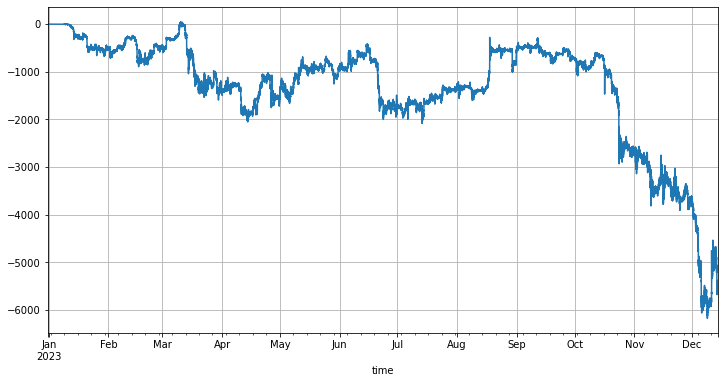

まず戦略を起動すると,回転価格を起動価格の1.6倍に設定し,ネット戦略は価格が1.6倍から現在の価格に下がる時に,この部分差が生じた多位を保持し,後者の価格が回転価格/1.6を超えると,初期価格をリセットし,常に少なくとも60%の差を保持します.回転テストの結果は以下のとおりです: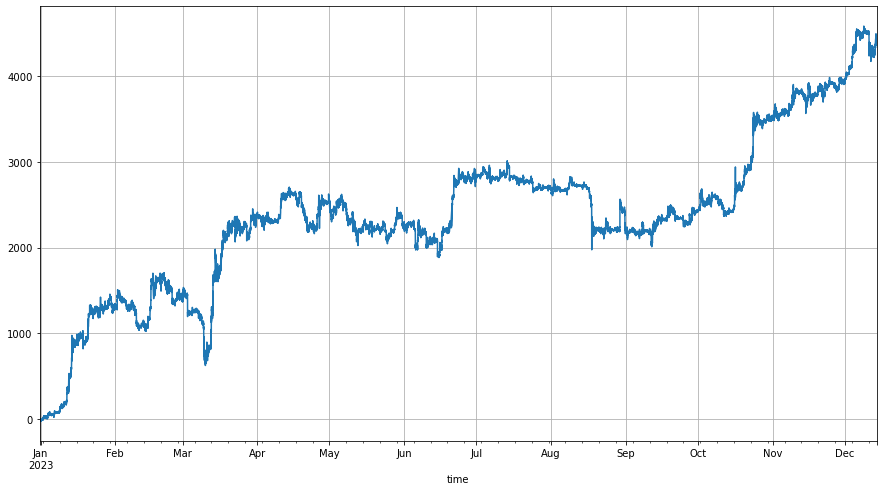

もちろん,市場が楽観的であれば,この比率をさらに大きく設定することができ,最終的に利益もそれに応じて上昇します. もちろん,市場が下落した場合,この設定は持分リスクも増加します.