長期・短期ポジションのバランスのとれた株式戦略を順序よく調整する

長期・短期ポジションのバランスのとれた株式戦略を順序よく調整する

前回の記事 (https://www.fmz.com/bbs-topic/9862データと数学的分析を用いて取引戦略を作成し,自動化する方法を示しました.

ロング・ショートポジションバランス・エクイティ戦略は,取引対象のバスケットに適用されるペア取引戦略の自然な延長である.デジタル通貨市場や商品先物市場などの多くの種類と相互関係を持つ取引市場に特に適している.

基本原則

ロングショートポジションバランスエクティ戦略は,取引目標のバスケットを同時にロングとショートにする.ペア取引と同様に,どの投資目標が安価で,どの投資目標が高価かを決定する.違いは,ロングショートポジションバランスエクティ戦略は,どの投資目標が比較的安価か高価かを決定するために,すべての投資目標を株式選択プールに整理するということです.その後,ランキングに基づいてトップn投資目標をロングし,底部n投資目標を同じ金額でショートします (ロングポジションの総価値 =ショートポジションの総価値).

パア取引は市場中立の戦略だと言ったことを覚えていますか? 長期ショートポジションのバランスされた株式戦略にも同じことが当てはまります. なぜなら,長期と短期の対等な量は,戦略が市場中立のまま (市場の変動の影響を受けない) であることを保証します. 戦略は統計的にも堅牢です. 投資目標をランク付けし,ロングポジションを保持することで,ランキングモデル上のポジションを1回だけではなく,何度もオープンすることができます. ランキングスキームの品質に純粋に賭けています.

ランキングは?

ランキングスキームは,期待されるパフォーマンスに応じて各投資対象に優先順位を割り当てることができるモデルである.要因は価値要因,技術指標,価格モデル,または上記のすべての要因の組み合わせである.例えば,動力指標を使用して,一連のトレンド追跡投資目標をランク付けすることができます.最も高い動力を持つ投資目標が引き続き良好なパフォーマンスを発揮し,最高ランクを取得することが期待されます.最小の動力を持つ投資対象は最悪のパフォーマンスと最低のリターンを持っています.

この戦略の成功は,ほぼ完全に使用されたランキングスキームに依存します.つまり,ランキングスキームは,ロングとショートポジション投資目標の戦略のリターンをより良く実現するために,高パフォーマンス投資目標と低パフォーマンス投資目標を分離することができます.したがって,ランキングスキームを開発することは非常に重要です.

ランキングをどうやって作るのか?

ランキングを決定すると,利益を得ることを期待します.上位投資目標に長額,下位投資目標に短額で同じ資本を投資することで,この戦略はランキングの品質に比例して利益を得ることを保証します.そしてそれは"市場中立"になります.

すべての投資目標 m をランク付けすると仮定し,投資に n ドルがあり,合計 2p (m> 2p) のポジションを保持したいとします.投資対象ランク 1 が最悪なパフォーマンスを期待される場合,投資対象ランク m が最も良いパフォーマンスを期待されます.

• 2/2p USDの投資目標を短縮します. 投資対象は,

• 投資対象は m-p,...,mポジション,n/2pUSDの投資目標に走ります.

注: 価格変動による投資対象物の価格が常に n/2p を均等に分割するものではなく,一部の投資対象物が整数で購入されなければならないため,この数値に可能な限り近い不正確なアルゴリズムがある. n=100000 と p=500 を実行する戦略では,以下のように見ることができます.

n/2p = 100000/1000 = 100

これは,価格が100を超えるスコア (商品先物市場など) に大きな問題をもたらすでしょう. なぜなら,あなたは割引価格でポジションを開くことはできません (この問題はデジタル通貨市場で存在しない). 私たちは割引価格取引を減らすか資本を増やすことでこの状況を緩和します.

仮説的な例を挙げましょう

• FMZ Quant プラットフォーム上で研究環境を構築する

まず第一に,スムーズに作業するためには,研究環境を構築する必要があります.この記事では,FMZ Quantプラットフォームを使用します (FMZ.COM) の研究環境を構築し,主に便利で高速な API インターフェースとこのプラットフォームのよくパッケージ化された Docker システムを後日利用します.

FMZ Quantプラットフォームの公式名称では,このDockerシステムはDockerシステムと呼ばれています.

ドッカーとロボットの展開について 私の前の記事を参照してください:https://www.fmz.com/bbs-topic/9864.

ドーカーを展開するために独自のクラウドコンピューティングサーバを購入したい読者は,この記事を参照してください:https://www.fmz.com/digest-topic/5711.

次に,Pythonの現在の最大のアーティファクトをインストールします. Anaconda.

この記事で要求されるすべての関連するプログラム環境 (依存ライブラリ,バージョン管理など) を実現するために,最も簡単な方法は Anaconda を使用することです.これはパッケージ化された Python データサイエンスエコシステムと依存ライブラリマネージャです.

アナコンダのインストール方法については,アナコンダの公式ガイドを参照してください.https://www.anaconda.com/distribution/.

この記事では,Python科学コンピューティングにおける 2つの人気のある重要なライブラリである numpy と pandas も使用します.

上記の基本作業は,Anaconda環境とnumpyとpandaライブラリを設定する方法について紹介する私の以前の記事にも言及することができます.詳細については,以下を参照してください:https://www.fmz.com/digest-topic/9863.

ランダムな投資目標と ランダムな要素を生成して 順位付けします

import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
## PROBLEM SETUP ##
# Generate stocks and a random factor value for them
stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)
# Generate future returns for these are dependent on our factor values
future_returns = current_factor_values + np.random.normal(0, 1, 10000)
# Put both the factor values and returns into one dataframe
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

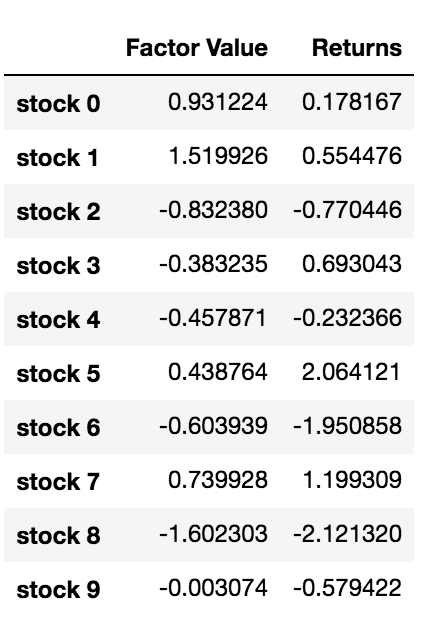
投資目標の順位を設定して ロング・ショート・ポジションを開くとどうなるか 分かります

# Rank stocks
ranked_data = data.sort_values('Factor Value')
# Compute the returns of each basket with a basket size 500, so total (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)
for i in range(number_of_baskets):
    start = i * 500
    end = i * 500 + 500 
    basket_returns[i] = ranked_data[start:end]['Returns'].mean()
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

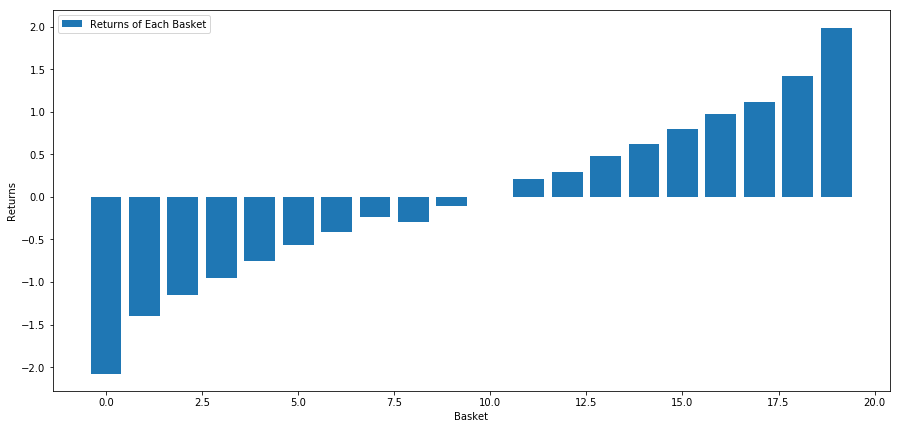
投資目標プールで第1位を長引く 10位を短引く戦略です この戦略の収益は以下の通りです

basket_returns[number_of_baskets-1] - basket_returns[0]

結果は 4.172 です.

高性能投資目標と低性能投資目標を 区別できるように ランキングモデルに投資します

この記事の残りの部分では,ランキングスキームの評価方法について説明します.ランキングベースのアービタージの利点は,市場混乱の影響を受けず,代わりに市場混乱が利用できるということです.

リアルな例を見てみましょう.

S&P500指数の 32の株のデータを 読み込み ランク付けしようとしました

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
                'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
                'HD','LOW','KO','LLY','MCD','MET','NEM',
                'PEP','PG','M','SWN','T','TGT',
                'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
price = 'adjClose'

ランキングの基礎として 1ヶ月間の標準化モメント指標を使用しましょう.

## Define normalized momentum
def momentum(dataDf, period):
    return dataDf.sub(dataDf.shift(period), fill_value=0) / dataDf.iloc[-1]
## Load relevant prices in a dataframe
data = ds.getBookDataByFeature()['Adj Close']
#Let's load momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

株価が市場でどう動いているか 分析します 株価が市場でどう動いているか 分析します

データを分析する

株式の行動

選択した株のバスケットがランキングモデルでどのように機能するか見てみましょう.これを行うために,すべての株の週間の先行リターンを計算しましょう.その後,各株の1週間の先行リターンと前30日の勢力の間の相関を見ることができます.ポジティブな相関を示した株はトレンドフォロワーであり,負の相関を示した株は平均逆転です.

# Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = True)
# Calculate correlations between momentum and returns
correlations = pd.DataFrame(index = returns.columns, columns = ['Scores', 'pvalues'])
mscores = mscores[mscores.index.isin(returns.index)]
for i in correlations.index:
    score, pvalue = stats.spearmanr(mscores[i], returns[i])
    correlations[‘pvalues’].loc[i] = pvalue
    correlations[‘Scores’].loc[i] = score
correlations.dropna(inplace = True)
correlations.sort_values('Scores', inplace=True)
l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations['Scores'])
plt.xlabel('Stocks')
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.legend(['Correlation over All Data'])
plt.ylabel('Correlation between %s day Momentum Scores and %s-day forward returns by Stock'%(day,forward_return_day));
plt.show()

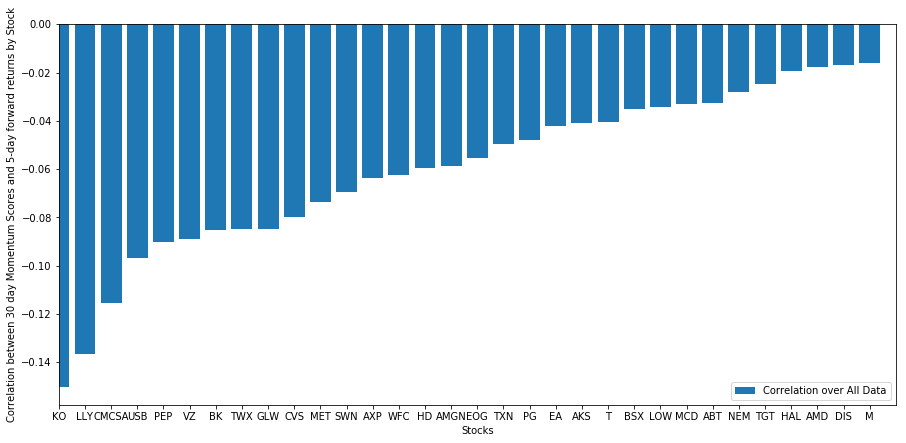
(明らかに,我々が選んだ宇宙はこんなふうに機能します.) これは,もし株がモメント分析でトップにランクインすれば,来週は不良のパフォーマンスを期待すべきだと教えてくれます.

モメント分析スコアとリターンのランキングとの相関

次に,ランキングスコアと市場の全体的な先行リターンの間の相関,つまり予測されたリターン率とランキングファクタルの間の関係を見なければなりません.より高い相関レベルがより低い相対的リターンを予測できるのか?

30日間の動向と1週間の先行リターンの間の 日々の相関を計算します

correl_scores = pd.DataFrame(index = returns.index.intersection(mscores.index), columns = ['Scores', 'pvalues'])
for i in correl_scores.index:
    score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
    correl_scores['pvalues'].loc[i] = pvalue
    correl_scores['Scores'].loc[i] = score
correl_scores.dropna(inplace = True)
l = correl_scores.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correl_scores['Scores'])
plt.hlines(np.mean(correl_scores['Scores']), 1,l+1, colors='r', linestyles='dashed')
plt.xlabel('Day')
plt.xlim((1, l+1))
plt.legend(['Mean Correlation over All Data', 'Daily Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

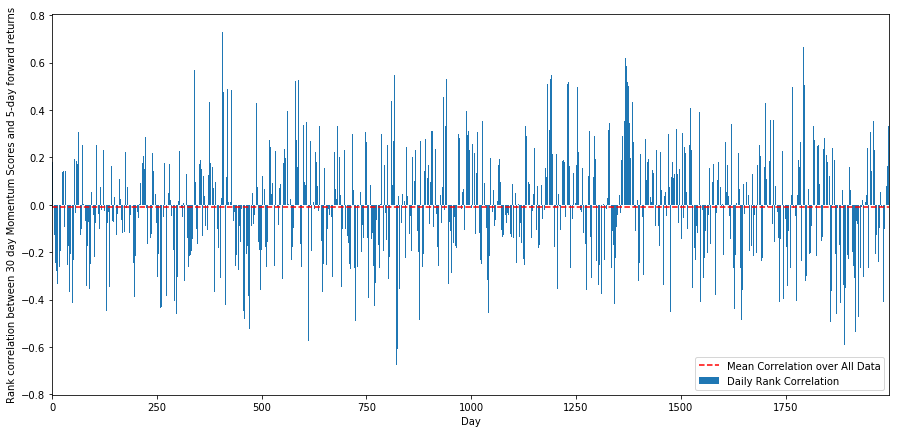
日々の相関は非常に複雑ですが,非常に微妙な相関を示しています (すべての株が平均に戻ると言ったので,それは予想されます).また,1ヶ月間の先行リターンの平均月間相関を見なければなりません.

monthly_mean_correl =correl_scores['Scores'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colors='r', linestyles='dashed')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

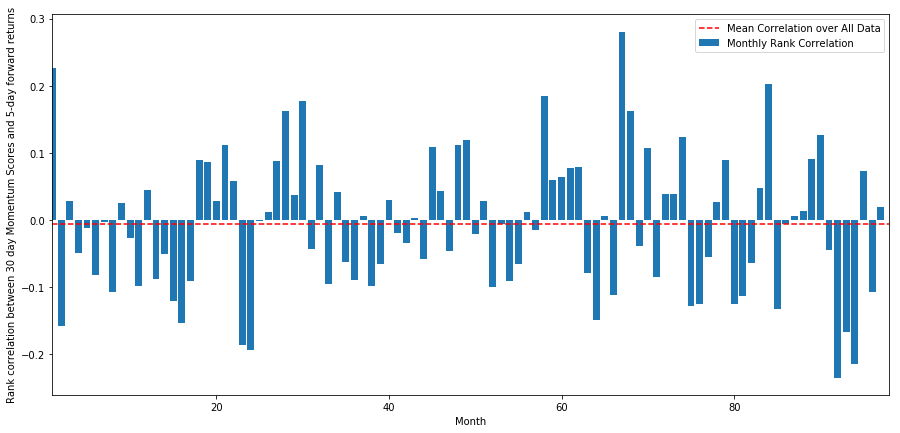
平均的な相関は再び少しマイナスですが 毎月大きく変化しています

株式のバスケットの平均収益

すべての株をランク付けし,nnグループに分けると,それぞれのグループの平均収益は?

最初のステップは 毎月与えられた各カートの平均収益率とランキングファクタを 示す関数を作成することです

def compute_basket_returns(factor, forward_returns, number_of_baskets, index):
data = pd.concat([factor.loc[index],forward_returns.loc[index]], axis=1)
    # Rank the equities on the factor values
    data.columns = ['Factor Value', 'Forward Returns']
    data.sort_values('Factor Value', inplace=True)
    # How many equities per basket
    equities_per_basket = np.floor(len(data.index) / number_of_baskets)
basket_returns = np.zeros(number_of_baskets)
# Compute the returns of each basket
    for i in range(number_of_baskets):
        start = i * equities_per_basket
        if i == number_of_baskets - 1:
            # Handle having a few extra in the last basket when our number of equities doesn't divide well
            end = len(data.index) - 1
        else:
            end = i * equities_per_basket + equities_per_basket
        # Actually compute the mean returns for each basket
        #s = data.index.iloc[start]
        #e = data.index.iloc[end]
        basket_returns[i] = data.iloc[int(start):int(end)]['Forward Returns'].mean()
        
    return basket_returns

このスコアに基づいて 株をランク付けすると 各バスケットの平均収益を計算します これは長期間に渡って その関係性を 理解できるようにします

number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(float).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = True)
for m in forward_returns.index.intersection(resampled_scores.index):
    basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
    mean_basket_returns += basket_returns
mean_basket_returns /= l    
print(mean_basket_returns)
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

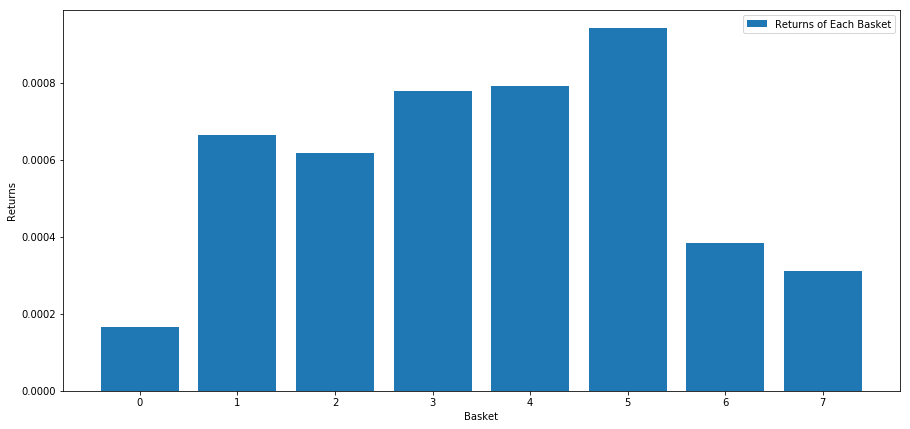
高い成績を上げている人と 低い成績を上げている人を 区別できるようです

マージン (ベース) の一貫性

もちろん,これらは平均的な関係に過ぎません.関係がどの程度一貫しているか,そして私たちが取引する意思があるかどうかを理解するために,私たちは時間とともにそれに対するアプローチと態度を変えなければなりません.次に,前2年間の月間利息率 (ベース) を見ていきます.より多くの変化を見ることができ,このモメントスコアが取引可能かどうかを決定するためにさらなる分析を行います.

total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
    temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[month]]
    temp_scores = resampled_scores.loc[monthly_index[month-1]:monthly_index[month]]
    for m in temp_returns.index.intersection(temp_scores.index):
        basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
        mean_basket_returns += basket_returns
    
    strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
    
    mean_basket_returns /= temp_returns.index.intersection(temp_scores.index).size
    
    r = int(np.floor((month-1) / 6))
    c = (month-1) % 6
    axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
    axarr[r, c].xaxis.set_visible(False)
    axarr[r, c].set_title('Month ' + str(month))
plt.show()

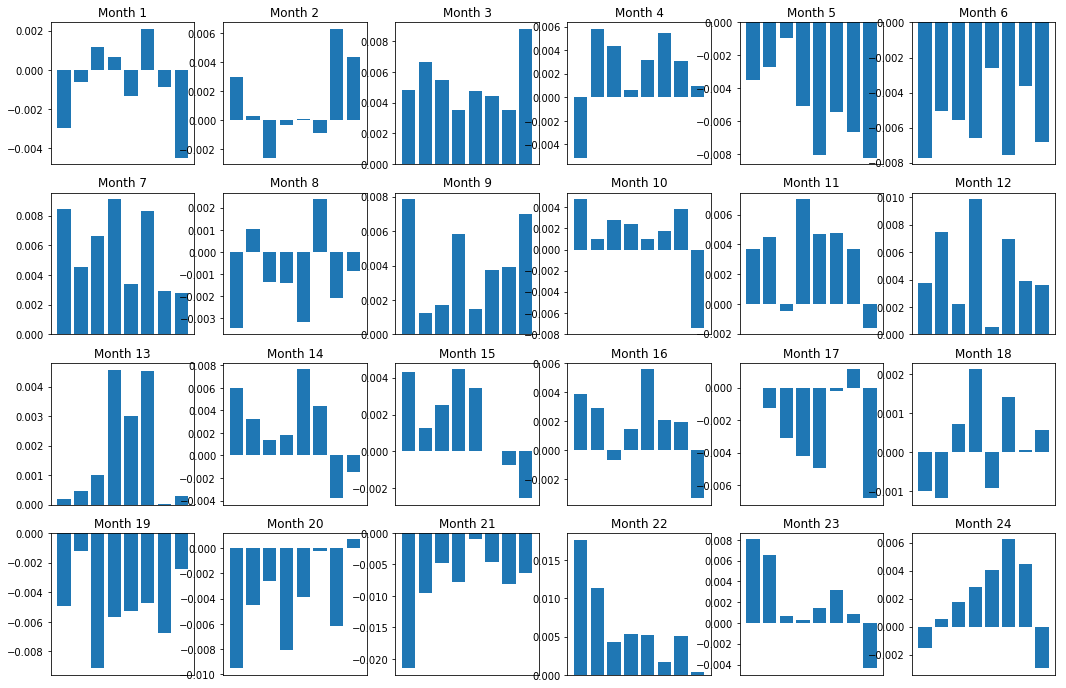
plt.figure(figsize=(15,7))
plt.plot(strategy_returns)
plt.ylabel('Returns')
plt.xlabel('Month')
plt.plot(strategy_returns.cumsum())
plt.legend(['Monthly Strategy Returns', 'Cumulative Strategy Returns'])
plt.show()

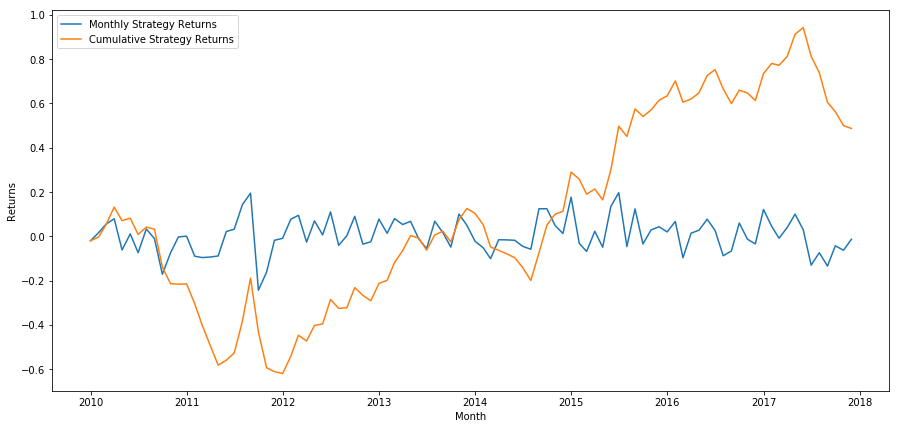
最後に,最後のバスケットをロングで,最初のバスケットをショートにすると,毎月,収益を見ます (証券ごとに同じ資本配置を仮定します).

total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

年間収益率: 5.03%

高性能株と低性能株の区別は 微妙にしかできない ランキングシステムがあることがわかります さらに このランキングシステムは一貫性がないし 毎月大きく変化しています

適切なランキング・スキームを見つける

長期・短期バランスエクティ戦略を実現するために,実際には,ランキングスキームを決定するだけです.それ以降のすべてが機械的です.長期・短期バランスエクティ戦略ができれば,多くの変化なしに異なるランキング因子を交換することができます.それはすべてのコードを調整する心配なしにアイデアを迅速に繰り返す非常に便利な方法です.

ランキング・スキームは,ほぼあらゆるモデルから来ることもできます.必ずしも価値ベースのファクターモデルではありません. 1ヶ月前にリターンを予測し,このレベルに従ってランク付けできる機械学習技術です.

ランキング制度の選択と評価

ランキング・スキームは,長期・短期間のバランス・エクチュア・戦略の利点であり,最も重要な部分です.良いランキング・スキームを選択することは,体系的なプロジェクトであり,簡単な答えはありません.

既存の既知の技術を選択し,より高い収益を得るためにそれらをわずかに修正できるかどうかを確認することです.ここでいくつかの出発点について議論します:

• クローンと調整: よく議論されているトピックを選択し,利点を得るために少し修正できるか確認します. 一般的に,公開されている要因は,完全に市場から仲裁されたため,もはや取引信号を持っていません. しかし,時には正しい方向にあなたを導くでしょう.

• 価格モデル: 将来の収益を予測するどのモデルも,取引対象のバスケットをランク付けするために潜在的に使用できる要因である可能性があります. 複雑な価格モデルを取り,ランキングスキームに変換することができます.

• 価格ベースの要因 (技術指標):今日議論されているように,価格ベースの要因は,各株式の歴史的価格に関する情報を入手し,因子値を生成するために使用します.例として,移動平均指標,モメント指標,または変動指標があります.

• リグレッションとモメンタム: いくつかの要因は,価格が1つの方向に動くと,そうし続けると信じているが,いくつかの要因は正反対であることに注意する.どちらも異なる時間軸と資産のための効果的なモデルであり,基本的な行動がモメンタムまたはリグレッションに基づいているかどうかを研究することが重要です.

• 基本要素 (価値に基づく):PE,配当など基本価値の組み合わせです. 基本価値には,会社の現実世界事実に関連する情報が含まれていますので,多くの点で価格よりも強力です.

最終的には,開発予測は軍拡競争であり,あなたは一歩先を行くことを試みています.要因は市場から仲介され,有用寿命がありますので,あなたは常にあなたの要因が経験した景気後退の数とそれらを置き換えるために使用できる新しい要因を決定するために働かなければならない.

その他の考慮事項

• 再バランスの頻度

各ランキングシステムは少し異なる時間枠でリターンを予測する.価格に基づく平均回帰は数日で予測可能であり,値に基づく因子モデルは数ヶ月で予測可能である.モデルは予測すべき時間範囲を決定し,戦略を実行する前に統計的検証を行うことが重要です.もちろん,再バランス周波数を最適化しようとすることで過度にフィットしたくない.あなたは必然的に他の周波数よりも優れたランダム周波数を見つけるでしょう.ランキングスキーム予測の時間範囲を決定した後,モデルを完全に利用するためにこの周波数で再バランスしようとします.

• 資本能力と取引コスト

各戦略には最小額と最大額の資本額があり,最低額は通常,取引コストによって決定されます.

株式の取引は,取引コストが高くなる. 1,000株を購入したい場合,リバランスごとに数千ドルかかります. 戦略が生み出す収益のわずかな部分を取引コストが占めるように,資本基盤が十分に高くなければなりません. 例えば,資本が10万ドルで戦略が月に1% (1,000ドル) を稼いでいる場合,これらの収益はすべて取引コストによって消費されます. 1,000株以上の収益を得るために,何百万ドルの資本で戦略を実行する必要があります.

最低の資産限界は主に取引された株の数に依存する.しかし,最大容量は非常に高い.長期短期バランス型株式戦略は,優位性を失うことなく数百百万ドルの取引が可能である.これは事実である.この戦略は,再バランスが比較的まれであるためである.総資産を取引された株数で割ると,各株のドル値は非常に低くなります.取引量が市場に影響するかどうか心配する必要はありません.あなたが1,000株,すなわち10万ドルを取引しているとします.毎月ポートフォリオ全体を再バランスした場合,各株は月に10万ドルしか取引されません.これはほとんどの証券にとって重要な市場であるのに十分ではありません.

関連性

もっと