高頻度取引から期待される収益

まとめ

高頻度取引におけるアルファの定義は、すべての戦略が価格に基づいて予測を行うわけではなく、より多くの条件とそれらの相互作用の理解が必要となるため、低頻度取引よりも複雑です。本稿では、HFT の構成要素と HFT 戦略の実装に使用される取引戦略を説明することにより、HFT のアルファ帰属モデルを開発します。結果は、高頻度取引業者がプラスの期待収益を生み出すためには迅速である必要があること、そして高頻度取引業者が流動性の提供に優れている理由を示唆している。高頻度株式データのサンプルを使用した実装例を示します。

高頻度取引（HFT）では、期待収益がプラスであることが収益性の鍵となります。多くの場合、この期待値はアルファと呼ばれます。人間のトレーダーと比較したアルゴリズム戦略の際立った特徴は、アルファの一貫性とアルファが達成される頻度です。低頻度取引に関する投資文献では、αはボラティリティと情報係数（IC）とZスコアの積に等しく、これは予測シグナルの信頼性の尺度である（グリノルド[（1994年）ただし、HFT でのアルファの定義は少し複雑です。すべての戦略が価格予測に基づいているわけではなく、より多くの条件とそれらの相互作用の理解が必要になるためです。

本稿では、高頻度取引のためのアルファ帰属モデルを開発します。アルファの構成要素と、HFT 戦略を実装するために使用される取引戦略を説明することでこれを行います。これらのコンポーネントには以下が含まれます。

1. チャンス
2. 得る
3. 有効スプレッド
4. 有効な割引。

さらに、高頻度株式データのサンプルを使用した実装例も提供します。

HFTのアルファ

HFT 業界では、アルファを絶対収益 1 と定義することがよくあります。バックテストまたはシミュレートされた取引によって生成された平均絶対収益（取引ごとまたは単位時間あたり）は、正確にはバックテスト アルファまたはシミュレートされたアルファと呼ばれます。もちろん、バックテストやシミュレートされたアルファは、将来のアルファ（つまり、戦略が実行された後）を信じる根拠として使用されます。これらのアルファを構成要素に分解することで、取引戦略を改善したり、よくあることですが、戦略が期待されたパフォーマンスから逸脱した理由を事後分析したりできるようになります。

おそらく、高頻度戦略の観点から見ると、低頻度戦略と同様に、利益は主に市場の非効率性を排除することによって得られます。その際、すべての投資戦略に影響を与える同じ基本概念を認識しておく必要があります。それは、どれだけの機会をつかむことができるか、どれだけ獲得できるか、そしてそれを獲得するにはどれだけの費用がかかるかということです。この目的のために、HFT におけるアルファの体系的な研究に必要なコンポーネントを定義します。

機会（O）

アルファに関するあらゆる議論の出発点は、利用可能な価格変動または機会 (O) です。特定の保有期間が与えられている場合、その期間中の価格変動は利用可能な利益を表します。この変動を測定する一般的な方法は、ビッド価格とアスク価格の中間点の変化の標準偏差です2。市場への継続的な露出を必要とするポートフォリオ戦略の場合、標準偏差は確かに適切な尺度ですが、オポチュニスティックHFT戦略（特定の条件下でのみポジションに入る）の場合、別の機会尺度が適切である可能性があります（たとえば、先物取引では、90分の1パーセンタイル移動、または固定されたセント数やロット数など)。ただし、他の尺度がない場合は、偶然の代理として標準偏差を使用することをお勧めします。

ゲット（C）

キャプチャ © は、予測シグナルを除いて、より一般的には任意の戦略でキャプチャできる機会の割合として定義します。ポートフォリオ戦略の場合、利得はIC×zスコア（グリノルド[（1994年）は、予測収益と実際の実現収益の相関関係によって測定されることが多い。 IC は価格に基づいて予測を行うため、IC の値が負の値になると悪いことになります。ただし、HFT では相関以外の尺度の方が適切な場合があるため、C の負の値が許容されることもあります。固定収益の統計的アービトラージ戦略の場合、ヒット率などの指標の方が適している可能性があります。考え方としては、予測ベースの戦略は IC と（完全ではないにしても）密接に相関する正の C を持つべきであるのに対し、流動性条件ベースの戦略は別の C、おそらくはゼロ未満の C を持つ可能性があるということです。いずれにせよ、現在私たちが持っている 2 つの要素を考慮すると、取引戦略を検討する前に、アルファは単純に C×O、つまり 3 を獲得する機会になります。

有効スプレッド（SE）

低頻度取引では、求められる機会がはるかに大きいため、ビッド・アスク・スプレッドはアルファの構成要素として無視されることが多いです。しかし、HFTでは保有期間が短く、売買スプレッドがアルファに大きな影響を与えます。ビッド・アスク・スプレッド (S) は、ビッド価格 (つまり、すぐに売る必要がある人が受け取る価格) とアスク価格 (つまり、すぐに買う必要がある人が支払う価格) の差です。伝統的な意味では、ストール[[1978]によれば、これはマーケットメーカーが情報に精通したトレーダーと取引する際に逆選択のリスクを負うため、マーケットメーカーに支払われるプレミアムであると考えられています。機会主義的な取引戦略が利益をもたらすか損失をもたらすかは、実装された戦略によって決まります。

取引戦略とは、取引戦略が成行注文と指値注文を使用して金融商品のポジションを開始および終了する方法を指します。指値注文とは、帳簿上の最高買値（売値）よりも低い（高い）価格で取引する要求です。このような注文は、市場の一方側（買い側または売り側）に流動性を提供します。指値注文は受動的であり、価格設定された売り（買い）注文が一致するまで取引所の指値注文帳に残ります。成行注文とは、利用可能な最良の売り（買い）価格での即時取引の要求です。このような注文には流動性が必要であり、市場価格に基づいています。成行注文は、成行注文または帳簿上の最高売値を超える価格での指値注文になります。

ラウンドトリップ取引を作成するテイカー注文またはメーカー注文の組み合わせにより、3 つの取引戦略が定義されます。テイクテイク戦略では、2 つの市場性のある注文を使用して、市場ポジションを開始および終了します。メイク・テイク戦略では、ポジションに入るために指値注文を使用し、ポジションから出るために成行注文を使用します。 Make-Make 戦略では、指値注文を使用してポジションを開始および終了します。異なる戦略では、ビッド・アスク・スプレッド S の取引コストが異なります。テイク・テイク戦略では、各ラウンドトリップトランザクションのトランザクションコストは S の 1 倍になります。各往復トランザクションについて、Take-take 戦略によって生成されるトランザクション コストは S の 1 倍になります。 make-take 戦略の場合、各ラウンドトリップトランザクションのコストは 0 倍の S ですが、make-make 戦略では各ラウンドトリップトランザクションで S を獲得できます。

たとえば、図 1 に示すような単純な市場を考えてみましょう。記録上最高値となった内部市場では、ビッド 99、アスク 100 で、ビッド・アスク・スプレッドはわずか 1 でした。 （簡単にするために、これらのレベルでのボリュームは無視します。）ポジションを市場価格100で購入し、すぐに市場価格99で売却するテイクテイク戦略は、ビッドアスクのためだけに利益をもたらします。スプレッドS。コストは1ポイントの損失のみです。

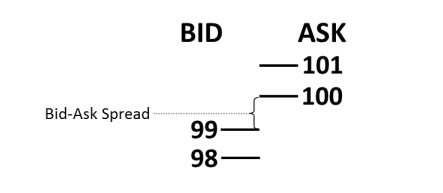
図1: ビッド・アスク・スプレッドによる簡略化された市場

メイクテイクを使用する取引戦略では、指値注文で 99 で購入し、その後すぐに市場価格で 99 で売却してポジションを終了すると、ビッド・アスク・スプレッドのコストは発生しません。最後に、メイクメイク取引戦略を使用して、指値注文でポジションに入り、99 ピップで買い、すぐにエントリーして後で指値注文で 100 ピップで売り、ビッド・アスク・スプレッド S を獲得します。これらの単純なシナリオから、式（1）の実効スプレッド（SE）値が導かれます。

有効リベート（RE）

株式市場では、取引所は通常、指値注文簿に指値注文を出して流動性を提供する取引会社に、リベート ® と呼ばれる手数料を支払います。流動性プロバイダーにインセンティブを与えることは、取引所にとって有益であると考えられています。より深く、より流動性の高い市場を持つことで、より多くの、より大きな機関投資家の流動性テイカーが集まり、取引量と取引手数料が増加するはずです。指値注文が執行または成立すると、取引会社は R を獲得します。したがって、リベートはアルファの重要な要素となる可能性があります。式（2）に示すように、取引戦略は実効リベート（RE）にも影響を与えます。テイクテイク戦略では指値注文を使用しないため、指値注文を使用する戦略ではリベートを受け取ることはできません。メイク・テイク戦略では往復ごとに 1 つのリベートを獲得できますが、メイク・メイク戦略では往復ごとに 2 倍の R を獲得できます。

期待収益率（α）

これら 4 つの要素を考慮すると、HFT 戦略のアルファは次のように完全に定義できます。

式（3）において、αは得られる機会から取引にかかる純コストを差し引いたものに等しい。 HFT では通常固定されている手数料とマージンを無視します。たとえば、証券会社は手数料を気にしておらず、市場に直接アクセスする高頻度取引業者は通常、株ごとに定額の手数料を支払います。これらが特定の企業にとって様々な戦略を決定する上で重要な変数である場合、式（3）に簡単に追加することができます。

戦略的重要性

式（３）の複雑な点は、各部分の値が相互に依存していることである。隠れた相互作用があります。これを考慮すると、取得機会は実効スプレッドから独立しているわけではありません。

1. 機会を捉えるということは、ポジションに素早くエントリーし、可能な限り最適なタイミングでそのポジションから抜け出す機能です。
2. 実効スプレッドは、使用される取引戦略に応じて異なります。すぐに実行して差額を支払うか、市場がパッシブ指値注文を実行するのを待って差額を稼ぐことができます。

したがって、効果的なスプレッドを得るためには、獲得した機会の一部を犠牲にする必要があります。あるいは、より多くの露出を得るには、実質的な差額を支払う必要があります。獲得率 C は実行速度とともに減少するため、この戦略は重要です。これら 3 つの方法で実装された取引戦略を検討すると、その戦略がアルファに与える影響がわかります。取引戦略には以下の特性があると想定します。

• 平均保留時間は60秒でした。
• 平均ビッド・アスク・スプレッド S は 0.08、つまり 8 セントです。
• 保持期間が 60 秒の場合、標準偏差 O60 の確率は 0.09、つまり 9 セントになります。
• R は 0.001、つまり 1 ペニーの 10 分の 1 です。

例1: テイクテイク

戦略がテイクテイク戦略を使用する場合、有効スプレッド SE は 0.08、RE は 0 になります。 C が 0.25 の場合、戦略のアルファは -0.0575 になります。 Take-take戦略を採用すると、すべてのC×Oが即座に実行され、獲得されますが、-Sが生成されます。したがって、収益性の高い戦略を立てるには、C×O が S より大きくなければなりません。

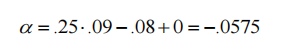
例 2: メイク・テイク

戦略がメイク・テイク戦略を使用する場合、有効スプレッド SE は 0、RE は 0.001 になります。 C が 0.10 に減少した場合、戦略の α は 0.01 になります。メイク・テイク戦略では –S は発生しませんが、取引を開始する前に不明な遅延が発生します。実行の遅延と逆選択により、C 値が低下しました。したがって、戦略の中でメイク・テイク戦略を使用するトレーダーは、指値注文キューで待機する時間を最小限に抑えるように努めるべきです6。

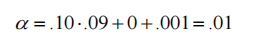
例3: メイクメイク

戦略がメイクメイク戦略を使用する場合、有効スプレッド SE は -0.08、RE は 0.002 になります。 C が -0.05 の場合、戦略のアルファは 0.0775 になります。 C の値は、両当事者の待機時間と両当事者の逆選択によりさらに減少します。この場合、C は負ですが、スプレッドとリベートにより期待値は正になります。メイクメイク戦略は、Sの量と2×Rの待機時間によって補正されるため、Cが負であっても、戦略のαは依然として正になります。

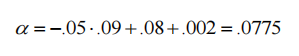
この状況は、流動性提供戦略にとって明るい見通しを示しています。この戦略は、逆選択イベントが発生したときに極端な左テールのリターンを生み出す可能性があることを考慮していません。これは、テクノロジーが遅い場合に特に当てはまります。 （これについては後で詳しく説明します。）この状況は、非常に短い保有期間とC値をゼロに近づけた新しい取引戦略につながり、どちらも逆選択を減らすのに役立ちます。確率なので、αは–S+です。 RE.例 3 は、HFT 戦略が低頻度取引よりも流動性の提供に優れている理由を示しています。低頻度トレーダーは大きな O 値を必要とし、負の C 値は不利です。 HFT 戦略は O 値が小さいため逆選択を回避でき、安定して –S+RE を獲得できます。

実証データ7と結果

式（1）の特性と様々な戦略がαに与える影響を示すために、2012年1月3日のApple Inc.（AAPL）のデータを使用しました。 (さまざまな例を試しましたが、結果は質的に変化しませんでした。) データセットには、すべての追加、キャンセル、実行を含む、Nasdaq 指値注文簿のすべてのイベントに関するすべての情報が含まれています。この情報にはナノ秒単位のタイムスタンプが付けられているため、すべてのイベントの正確な時間および順序を計算できます。このデータを使用して、時間の経過に伴う中間入札価格の変化の標準偏差を使用して確率 O を計算します。

今説明したデータを使用すると、その日の平均ビッド・アスク・スプレッド S は 0.088704、つまり約 9 セントになります。異なる保有期間における USD の標準偏差を図 2 に示します。

図2: 保有期間別の標準偏差

図2の標準偏差を機会の代理として使用し、αを計算して式（3）に従ってCの値を取得します。値は-1から1の範囲です。 （C = 1の場合、論理的にはカーンズらの「全知のトレーダー」と同等である。[[2010]。 )R=0と仮定します。図 3、4、5 は、異なる保有期間における 3 つの戦略のアルファを示しています。例えば、図3では、保有期間が1秒、C = -1.00、O = 0.0199、S = 0.088704、R = 0の場合、テイク・テイク戦略ではαの値は-0.109となり、左上隅に表示されます。表示。図3～5のグラフでは、網掛けされたセルはαの値が正であることを示しています。他のすべてのセルでは、α は負または 0 です。

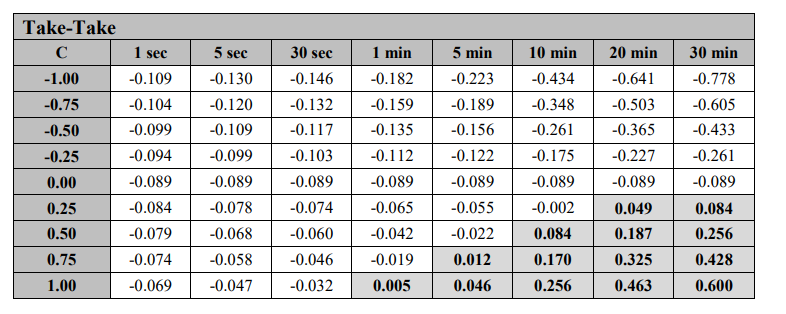
図3: AlphasによるTake-Take戦略

図 3 では、テイクテイク戦略の場合、少なくとも HFT 基準では、C 値が信じられないほど高い場合 (つまり、0.75 または 1.00)、または保有期間が非常に長い場合にのみ、α が正になることがわかります。実際には、高い C 値は、つかの間の機会を追う戦略で使用できます。価格予測に依存する戦略の場合、約 0.25 を超える C 値を見つけるのは困難であり、20 ～ 30 分の保有期間は高頻度の定義から外れる可能性が高くなります。この組み合わせにより、HFT 戦略ではテイク・テイク戦略を使用してプラスのアルファを達成することが非常に困難になります。ビッド・アスク・スプレッドのコストは、より優れた予測によって短期間で克服することは困難です。

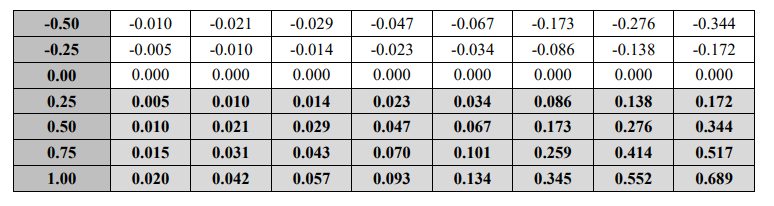
図4: AlphasによるMake-Take戦略

図 4 では、make-take 戦略の場合、α は任意の正の値に対して常に正であることがわかります。これは非常に明らかです。なぜなら、S = 0 の場合、正の獲得は正の α をもたらし、負の獲得は負の α をもたらすからです。ただし、暗黙の前提として、実行を待機するキュー内で費やされる時間は短いとされています。注文は数秒、あるいは数分間キュー内に留まることが多く、この時間枠内でアルファを取得することができなくなります。もちろん、人のスキルが速ければ速いほど、順番は順番が早くなり、待ち時間も短くなります。したがって、スピードにより、トレーディング会社はより短い期間でアルファを達成できるようになります。図 4 のもう 1 つの暗黙の仮定は、C の値が時間の経過とともに一定のままであるというものですが、これはここで示す結果では確かに当てはまりません。

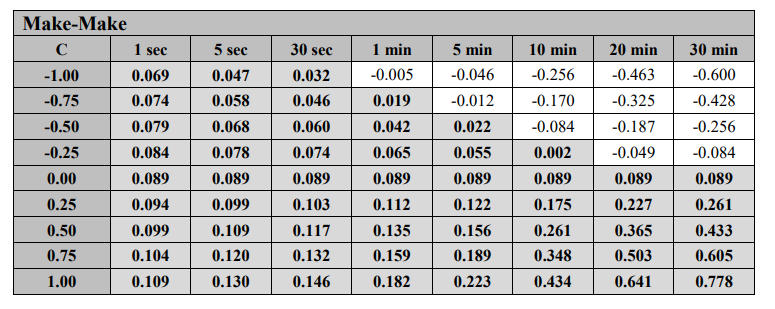
図5: AlphasによるMake-Make戦略

図5では、make-make戦略の場合、Cのほぼすべての値でαが正であることがわかります。 C値がマイナスの場合でも、技術的なスピードが速ければ、獲得した差額の価値は、どんなに下手な戦略でも基本的に克服できます。前の例と同様に、保有期間の短縮に伴うプラスのアルファを達成するには、指値注文を迅速に実行できるかどうかが重要です。これは、待ち時間が非常に短い場合、つまり常に列の先頭にいる場合にのみ一貫して発生します。キューの最後尾にいるということは、実行を長時間待つことを意味し、待機時間が長くなるほど、逆選択が発生する可能性が高くなります8。

スピードの影響

テクノロジーのスピードは、利用できる機会に大きな影響を与えます。まず、図 6 に示すように、予測と実際の価格変動の相関関係は時間の経過とともに低下します。この減衰は予測の長さの関数です。図 6 は、10 分の 1 秒の遅延に対する 1 秒および 5 秒の予測の減衰を示しています。したがって、実行の遅延はフェッチに悪影響を及ぼします。したがって、多くの取引戦略は、十分な速さで取引を行うために必要な固定技術コストの観点からメイクメイク戦略を使用するには費用がかかりすぎるため、またはテイクテイク戦略を使用するには費用がかかりすぎるため、適格とならない。スプレッドコストの。

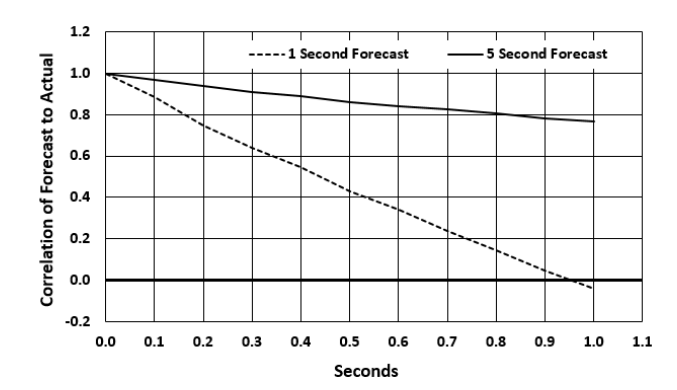
図6: 時間の経過に伴う予測の減衰

第二に、実行の遅延は実現機会の計算に影響を及ぼす可能性があります。速度が遅い場合は、列の最後尾に配置されます。キューの最後尾にある取引は、情報に基づいた取引（間違った方向）よりも実行される可能性が高くなります。逆選択の確率は高くなり、実現の可能性は単純な標準偏差が示唆するよりも悪くなります。これは、獲得 C がマイナスの戦略にとっては残念なことです。累積損失を止めるにはテイクトレードが必要になる可能性があり、メイクメイク戦略よりも実効スプレッドが悪くなる可能性があります。したがって、非常に速いプレーヤーを除いて、図 5 のメイクメイク戦略を使用する戦略の収益性は幻想的です。

結論は

HFT 戦略は、複雑な期待収益の計算式に直面します。しかし、アルファを構成要素に分解することで、トレーディング会社は利益と損失の変動性をよりよく理解できるようになります。もちろん、この変動には成分の変動だけでなく、考慮しなければならない相関関係も含まれます。これらの接続により、速度の必要性が説明されます。テクノロジーのスピードは、急速な下降スパイラルを生み出すような大きな負の相関関係を構成要素が形成するのを防ぐのに役立ちます。アルファ方程式を理解することは、リスク管理者、戦略家、規制当局が HFT の複雑さを理解するのに役立ちます。

参考文献

Grinold, R. C. “Alpha is volatility times IC times score.” Journal of Portfolio Management, 20 (1994), pp. 9-16. Stoll, H. R. “The supply of dealer services in securities markets.” Journal of Finance, 33 (1978), pp. 1133-1151. Kearns, M., A. Kulesza, Y. Nevmyvaka. “Empirical limitations on high frequency trading profitability.” Journal of Trading, 5 (2010), pp. 50-62.

---

1. 一部の戦略では、ベンチマークに対する残余収益も含まれる場合があります。この場合、私たちのアプローチは簡単に適用できます。
2. 中間価格は、買値と売値の合計を 2 で割った値です。標準偏差は通常、対数リターンの標準偏差ですが、米ドルで表されます。
3. 低頻度戦略の場合、C × O は Grinold (1984) とまったく同じになります。
4. 買い指値注文の指値価格が現在の指値帳の最大指値価格以上である場合、その指値注文は取引指値注文帳には入れられませんが、市場売り価格で残りの指値注文とすぐにマッチングされます。
5. テイクメイク戦略は、HFT で使用されることはほとんどありません。
6. 価格と時間の優先順位を持つ先入れ先出し (FIFO) キューを想定します。
7. これらのデータを提供していただいたXambala, Inc.に感謝申し上げます。また、これらのデータを当社の研究で使用するためにNasdaqから許可を得ています。
8. 私たちがまだ対処していない複雑な問題の一つは、より広範な市場変動に関連する逆選択が投げ売りストップ取引につながる可能性があることです。これは、執行速度が重要であるもう一つの理由です。

元のアドレス: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2553582