프로그램적 트레이더를 위한 강력한 도구: 평균과 변수를 계산하기 위한 점진적 업데이트 알고리즘

소개

프로그램 트레이딩에서는 이동 평균 및 변동 지표와 같은 평균과 변동을 계산하는 것이 종종 필요합니다. 고주파 및 장기 계산이 필요할 때, 불필요하고 자원을 소비하는 역사 데이터를 오랫동안 보유하는 것이 필요합니다. 이 문서에서는 가중 평균과 변동을 계산하는 온라인 업데이트 알고리즘을 소개합니다. 이는 실시간 데이터 스트림을 처리하고 동적으로 조정하는 특히 고주파 전략의 거래 전략에 특히 중요합니다. 이 기사에는 트레이더가 알고리즘을 신속하게 배포하고 실제 거래에 적용하는 데 도움이되는 대응하는 파이썬 코드 구현도 제공됩니다.

단순 평균 및 변수

만약 우리가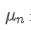n 번째 데이터 포인트의 평균 값을 나타내기 위해, 우리는 이미 n-1 데이터 포인트 / 업로드 / 자산 / 28e28ae0beba5e8a810a6.png의 평균을 계산했다고 가정합니다. 이제 우리는 새로운 데이터 포인트 / 업로드 / 자산 / 28d4723cf4cab1cf78f50.png를 얻습니다. 우리는 새로운 평균 수를 계산하고 싶습니다.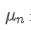새로운 데이터 포인트를 포함합니다. 다음은 자세한 파생입니다.

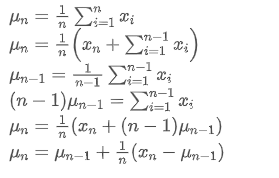
변동 업데이트 프로세스는 다음 단계로 나눌 수 있습니다.

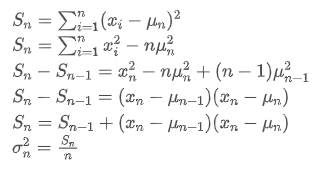
위의 두 공식에서 볼 수 있듯이, 이 과정은 새로운 데이터 포인트를 수신 할 때 새로운 평균과 변수를 업데이트 할 수 있습니다.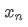이전 데이터의 평균과 변수를만 보존하여 역사적 데이터를 저장하지 않고 계산을 더 효율적으로 수행합니다. 그러나 문제는 이러한 방법으로 계산하는 것이 모든 샘플의 평균과 변수이며 실제 전략에서는 특정 고정 기간을 고려해야합니다. 위의 평균 업데이트를 관찰하면 새로운 평균 업데이트의 양이 새로운 데이터와 과거의 평균 사이의 오차가 비율로 곱된다는 것을 보여줍니다. 이 비율이 고정되면 기하급수적으로 가중된 평균으로 이어집니다. 다음으로 논의 할 것입니다.

기하급수적으로 가중된 평균

기하급수 중중 평균은 다음과 같은 재귀 관계로 정의될 수 있습니다.

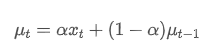
그 중에는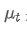시간점 t의 지수중량 평균,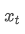시점 t에서 관찰된 값, α는 가중 인수, 그리고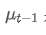이전 시간점의 지수중량 평균입니다.

기하급수적으로 가중된 변동

변동에 관해서는, 우리는 각 시점의 제곱 편차의 지수 중심을 계산해야 합니다. 이것은 다음과 같은 재귀 관계를 통해 달성될 수 있습니다.

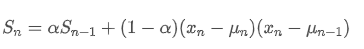
그 중에는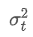시간점 t의 지수중량 변동, 그리고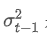이전 시간점의 지수중량 변동입니다.

기하급수적으로 가중된 평균과 변수를 관찰하십시오. 그들의 증수 업데이트는 직관적이며, 과거의 값의 일부를 유지하고 새로운 변화를 추가합니다. 특정 파생 프로세스는이 논문에서 참조 될 수 있습니다.https://fanf2.user.srcf.net/hermes/doc/antiforgery/stats.pdf

SMA와 EMA

SMA (수학적 평균으로도 알려져 있다) 와 EMA는 서로 다른 특성과 용도를 가진 두 가지 일반적인 통계 측정이다. 전자는 데이터 세트의 중심 위치를 반영하여 각 관찰에 동등한 무게를 부여한다. 후자는 더 최근의 관찰에 더 높은 무게를 부여하는 재귀 계산 방법이다. 무게는 현재 시간과의 거리가 증가함에 따라 기하급수적으로 감소한다.

• 무게 분포: SMA는 각 데이터 포인트에 동일한 무게를 부여하고, EMA는 가장 최근의 데이터 포인트에 더 큰 무게를 부여합니다.
• 새로운 정보에 대한 민감성: SMA는 모든 데이터 포인트를 재 계산해야 하기 때문에 새로 추가된 데이터에 충분히 민감하지 않습니다. 반면 EMA는 최신 데이터의 변화를 더 빠르게 반영할 수 있습니다.
• 계산 복잡성: SMA의 계산은 비교적 간단하지만 데이터 포인트 수가 증가함에 따라 계산 비용도 증가합니다. EMA의 계산은 더 복잡하지만 재귀성 특성으로 인해 연속 데이터 스트림을 더 효율적으로 처리 할 수 있습니다.

EMA와 SMA 사이의 대략적인 변환 방법

SMA와 EMA는 개념적으로 다르지만, 적절한 α 값을 선택하여 특정 수의 관측을 포함하는 SMA에 EMA를 근사시킬 수 있습니다. 이 근사 관계는 EMA의 무게 요인 α의 함수인 효과적인 표본 크기로 설명 할 수 있습니다.

SMA는 주어진 시간 창 내의 모든 가격의 수학적 평균이다. 시간 창 N의 경우, SMA의 중점 (즉 평균 숫자가 위치하는 위치) 은 다음과 같이 간주 될 수 있다.

SMA의 중동체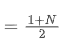

EMA는 가장 최근의 데이터 포인트가 더 큰 무게를 갖는 가중화 평균의 일종이다. EMA의 무게는 시간이 지남에 따라 기하급수적으로 감소한다. EMA의 중심을 다음과 같은 시리즈를 합쳐서 얻을 수 있다:

EMA의 중심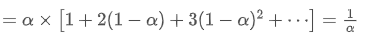

SMA와 EMA가 같은 중심을 가지고 있다고 가정하면

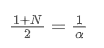
이 방정식을 풀기 위해, 우리는 α와 N 사이의 관계를 얻을 수 있습니다.

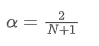
이것은 주어진 N 일간의 SMA에 대해 해당 α 값을 사용하여 동적 EMA를 계산할 수 있음을 의미합니다. 따라서 그들은 동일한 중심을 가지고 있으며 결과는 매우 비슷합니다.

다른 업데이트 주파수와 함께 EMA 변환

만약 우리가 EMA를 가지고 있다고 가정해 봅시다. EMA는 매초마다 업데이트되며, /upload/asset/28da19ef219cae323a32f.png의 가중 인수가 있습니다. 이것은 매초마다 새로운 데이터 포인트가 EMA에 추가될 것이고,

업데이트 주파수를 변경하면 f초에 한 번 업데이트하는 것과 같이 새로운 무게 인수를 /upload/asset/28d2d28762e349a03c531.png로 찾고자 합니다.

f초 이내에, 업데이트가 이루어지지 않으면, 오래된 데이터 포인트의 영향은 /upload/asset/28e50eb9c37d5626d6691.png로 곱한 f배로 지속적으로 붕괴됩니다. 따라서, f초 후에 전체 붕괴 인수는 /upload/asset/28e296f97d8c8344a2ee6.png입니다.

f초마다 업데이트되는 EMA가 한 업데이트 기간 내에 매초마다 업데이트되는 EMA와 동일한 붕괴 효과를 가져오기 위해, f초 후에 전체 붕괴 인수를 한 업데이트 기간 내에 붕괴 인자와 동일하게 설정합니다.

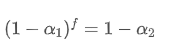
이 방정식을 풀면 새로운 무게 인수를 얻을 수 있습니다.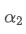

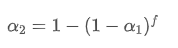
이 공식은 업데이트 주파수가 변경될 때 EMA 평형 효과를 변하지 않게 유지하는 새로운 가중 인수 / 업로드 / 자산 / 28d2d28762e349a03c531.png의 대략적인 값을 제공합니다. 예를 들어: 평균 가격을 계산할 때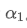값은 0.001이고 10초마다 업데이트합니다.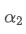대략 0.01이 될 것입니다.

파이썬 코드 구현

class ExponentialWeightedStats:
    def __init__(self, alpha):
        self.alpha = alpha
        self.mu = 0
        self.S = 0
        self.initialized = False

    def update(self, x):
        if not self.initialized:
            self.mu = x
            self.S = 0
            self.initialized = True
        else:
            temp = x - self.mu
            new_mu = self.mu + self.alpha * temp
            self.S = self.alpha * self.S + (1 - self.alpha) * temp * (x - self.mu)
            self.mu = new_mu

    @property
    def mean(self):
        return self.mu

    @property
    def variance(self):
        return self.S

# Usage example
alpha = 0.05  # Weight factor
stats = ExponentialWeightedStats(alpha)
data_stream = [] # Data stream
for data_point in data_stream:
    stats.update(data_point)

요약

높은 주파수 프로그램 트레이딩에서 실시간 데이터의 빠른 처리는 매우 중요합니다. 컴퓨팅 효율성을 향상시키고 자원 소비를 줄이기 위해, 이 기사는 데이터 스트림의 중량 평균과 변수를 지속적으로 계산하는 온라인 업데이트 알고리즘을 소개합니다. 실시간 인크리멘탈 업데이트는 또한 두 자산 가격 사이의 상관관계, 선형 적합성 등과 같은 다양한 통계 데이터 및 지표 계산에 사용할 수 있으며, 큰 잠재력을 가지고 있습니다. 인크리멘탈 업데이트는 데이터를 신호 시스템으로 취급하며, 이는 고정 기간 계산에 비해 사고의 진화입니다. 전략이 여전히 역사적 데이터를 사용하여 계산하는 부분을 포함하고 있다면 이러한 접근법에 따라 변환하는 것을 고려하십시오. 시스템 상태의 추정만 기록하고 새로운 데이터가 도착하면 시스템 상태를 업데이트하십시오. 앞으로이 주기를 반복하십시오.