위험과 수익을 측정하는 것 - 마르코비츠 이론에 대한 소개

지난주,포지션 리스크를 측정하는 방법 - VaR 방법의 소개, 포트폴리오의 위험은 개별 자산의 위험과 같지 않으며 가격 상관관계와 관련이 있다고 언급되었습니다. 두 가지 자산을 예로 들면, 긍정적 인 상관관계가 매우 강하다면, 즉 함께 상승하고 떨어지면 투자가 다양화되면 위험을 줄이지 않을 것입니다. 강한 부정적인 상관관계가 있다면, 다양화된 투자가 위험을 크게 줄일 수 있습니다. 그러면 자연스러운 질문이 발생합니다. 포트폴리오에 투자 할 때 특정 수준의 위험에서 수익을 극대화하는 방법은 무엇입니까? 이것은 우리를 오늘 소개 할 Markowitz 이론으로 이끌고 있습니다.

현대 포트폴리오 이론 (Modern Portfolio Theory, MPT) 은 1952년 해리 마르코비츠가 제안한 포트폴리오 선택에 대한 수학적 틀이다. 리스크를 제어하는 동시에 위험 자산의 다양한 조합을 선택함으로써 기대 수익을 극대화하는 것을 목표로 한다. 핵심 아이디어는 자산의 가격이 서로 완전히 동기화되지 않으며 (즉, 자산 사이에 불완전한 상관관계가 있으며), 전반적인 투자 위험은 다각화된 자산 할당을 통해 줄일 수 있다는 것이다.

마르코비츠 이론의 핵심 개념

1. 예상 수익률: 투자자가 보유 자산이나 투자 포트폴리오에서 기대하는 수익률입니다. 일반적으로 역사적인 수익 데이터에 기초하여 예측됩니다.

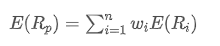
어디?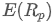포트폴리오의 예상 수익률입니다.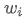포트폴리오의 i 번째 자산의 무게입니다.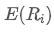i자산의 예상 수익률입니다.

2. 리스크 (변동성 또는 표준편차): 투자 수익의 불확실성 또는 투자 변동성을 측정하는 데 사용됩니다.

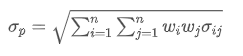
어디?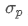포트폴리오의 전체 리스크를 나타냅니다.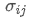자산 i와 자산 j의 상호변동성, 이 두 자산 사이의 가격 변화 관계를 측정하는 값입니다.

3. 동변성: 두 자산의 가격 변화 사이의 상호 관계를 측정합니다.

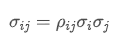
어디?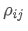자산 i와 자산 j의 상관률입니다.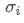그리고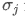각각 자산 i와 자산 j의 표준편차입니다.

4. 효율적 인 국경: 리스크-이익 조정 시스템에서 효율적 경계는 주어진 위험 수준에서 최대 기대 수익을 제공할 수 있는 투자 포트폴리오의 집합입니다.

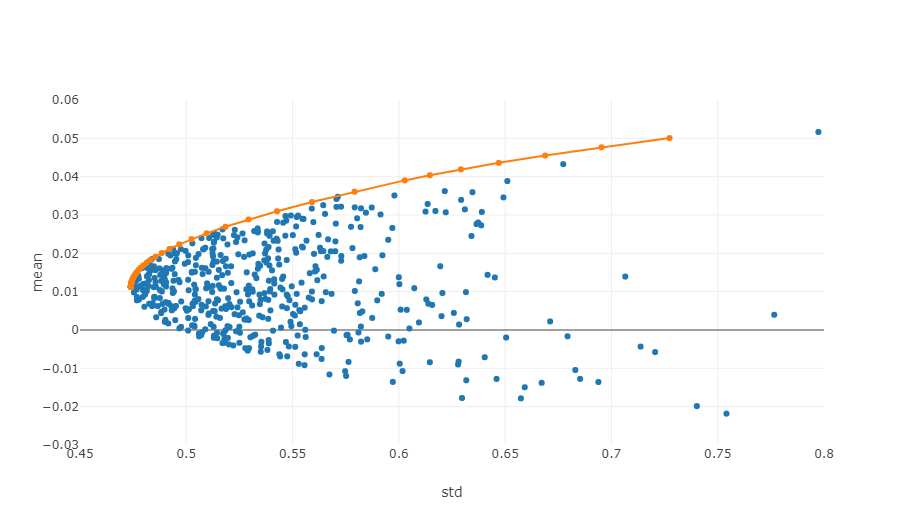
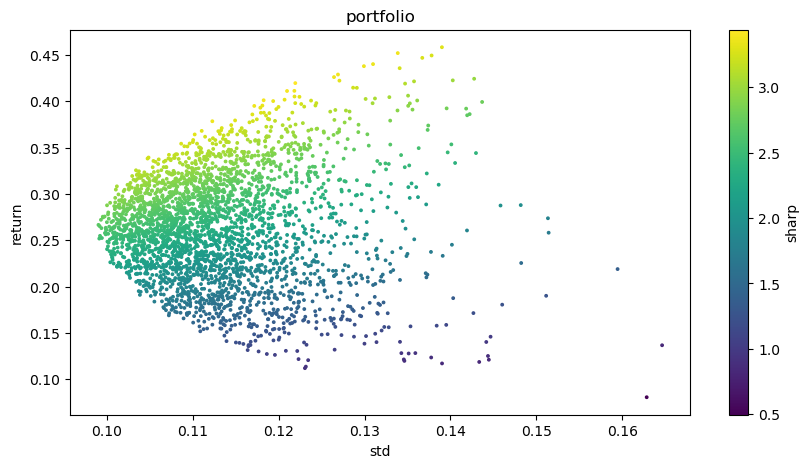
위의 도표는 효율적 경계의 예이며, 각 지점은 다른 가중된 투자 포트폴리오를 나타냅니다. x축은 위험 수준에 해당하는 변동성을 나타냅니다. y축은 수익률을 나타냅니다. 분명히 우리의 초점은 그래프의 상단에 있습니다. 이는 동등한 위험 수준에서 가장 높은 수익을 달성하기 때문입니다.

양적 거래 및 포트폴리오 관리에서 이러한 원리를 적용하려면 역사적 데이터의 통계 분석과 다양한 자산에 대한 예상 수익, 표준편차 및 covariances를 추정하기 위해 수학적 모델을 사용하는 것이 필요합니다. 다음으로 최적화 기술은 최상의 자산 무게 할당을 찾기 위해 사용됩니다. 이 프로세스는 종종 복잡한 수학적 연산과 광범위한 컴퓨터 처리를 포함합니다. 이것이 현대 금융에서 양적 분석이 매우 중요한 이유입니다. 다음으로 특정 파이썬 사례로 최적화하는 방법을 설명 할 것입니다.

시뮬레이션 방법을 사용하여 최적의 조합을 찾는 파이썬 코드 예

마르코비츠 최적 포트폴리오를 계산하는 것은 여러 단계의 과정이며, 데이터 준비, 포트폴리오 시뮬레이션 및 지표 계산과 같은 몇 가지 주요 단계가 포함됩니다. 참조하십시오:https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. 시장 데이터를 수집:

그 안에서get_data기능, 선택 된 디지털 화폐의 역사 가격 데이터를 얻습니다. 이것은 투자 포트폴리오를 구축하고 샤르페 비율을 계산하는 데 사용되는 수익과 위험을 계산하는 데 필요한 데이터입니다.

2. 수익률과 위험성 계산:

이calculate_returns_risk이 함수는 각 디지털 화폐에 대한 연간 수익과 연간 위험 (표준편차) 을 계산하는 데 사용되었습니다. 이것은 최적 포트폴리오에 사용하기 위해 각 자산의 역사적 성과를 정량화하기 위해 수행됩니다.

3. 마르코비츠 최적 포트폴리오를 계산합니다.:

이calculate_optimal_portfolio이 함수는 여러 투자 포트폴리오를 시뮬레이션하는 데 사용되었습니다. 각 시뮬레이션에서 자산 가중량은 무작위로 생성되고 그 후 포트폴리오의 예상 수익과 위험을 계산했습니다. 다른 무게를 가진 무작위로 조합을 생성함으로써 최적의 것을 찾기 위해 여러 잠재적 투자 포트폴리오를 탐구 할 수 있습니다. 이것은 Markowitz의 포트폴리오 이론의 핵심 아이디어 중 하나입니다.

전체 프로세스의 목적은 주어진 수준의 위험에서 가장 기대되는 수익을 창출하는 투자 포트폴리오를 찾는 것입니다. 여러 가지 가능한 조합을 시뮬레이션함으로써 투자자는 다른 구성의 성능을 더 잘 이해하고 투자 목표와 위험 관용에 가장 적합한 조합을 선택할 수 있습니다.이 방법은 투자 결정을 최적화하고 투자를 더 효과적으로 만드는 데 도움이됩니다.

import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# Obtain market data
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# Calculate Markowitz Optimal Portfolio
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # Convert weights to a list

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# Output results
print("Optimal combination:")
for i in range(len(symbols)):
    print(f"{symbols[i]} Weight: {optimal_weights[i]:.4f}")

print(f"Expected return rate: {optimal_return:.4f}")
print(f"Expected risk (standard deviation): {optimal_risk:.4f}")
print(f"Sharpe ratio: {optimal_return / optimal_risk:.4f}")

# Visualized investment portfolio
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

최종 출력 결과 최적의 조합: BTCUSDT의 무게: 0.0721 ETHUSDT 가중도: 0.2704 BNBUSDT의 가중도: 0.3646 LINKUSDT 가중치: 0.1892 BCHUSDT의 무게: 0.0829 LTCUSDT의 무게: 0.0209 기대 수익률 0.4195 예상 위험 (표준편차): 0.1219 샤프 비율: 3.4403