이전 기사에서 우리는 암호화폐 시장에서 흔히 나타나는 현상에 대해 살펴보았습니다. 대부분의 암호화폐, 특히 비트코인과 이더리움의 가격 변동을 따르는 암호화폐는 종종 함께 상승과 하락을 반복하는 추세를 보입니다. 이러한 현상은 주요 통화와의 높은 상관관계를 보여줍니다. 그러나 다양한 암호화폐 간의 상관관계 정도는 다릅니다. 그렇다면 이러한 상관관계의 차이는 각 통화의 시장 성과에 어떤 영향을 미칠까요? 이 글에서는 2023년 하반기의 강세장을 예로 들어 이 문제를 살펴보겠습니다.

암호화폐 시장의 동시성 뿌리

암호화폐 시장은 변동성과 불확실성으로 유명합니다. 비트코인과 이더리움은 시장의 두 거물로, 종종 가격 추세에서 주도적인 역할을 합니다. 시장 경쟁력과 거래 활동을 유지하기 위해 대부분의 소규모 또는 새롭게 부상하는 디지털 통화는 이러한 주류 통화, 특히 프로젝트 당사자가 만든 통화와 어느 정도 가격 동기화를 유지하는 경향이 있습니다. 이러한 동기화는 시장 참여자의 심리적 기대와 거래 전략을 반영하는데, 이는 양적 거래 전략을 설계하는 데 있어 중요한 고려 사항입니다.

상관관계 공식 및 계산 방법

양적 거래 분야에서는 통계적 방법을 통해 상관관계를 측정합니다. 가장 일반적으로 사용되는 측정 방법은 피어슨 상관계수인데, 이는 두 변수 사이의 선형 연관성의 정도를 측정합니다. 핵심 개념과 계산 방법은 다음과 같습니다.

피어슨 상관계수(기호 \(r\))는 -1에서 +1까지의 값을 가지는데, +1은 완벽한 양의 상관관계를 나타내고, -1은 완벽한 음의 상관관계를 나타내며, 0은 선형 상관관계가 없음을 나타냅니다. 계수는 다음과 같이 계산됩니다.

\(r = \frac{\sum_{i=1}^{n} (X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum_{i=1}^{n} (X_i - \bar{X})^2} \sqrt{\sum_{i=1}^{n} (Y_i - \bar{Y})^2}}\)

여기서, \(X_i\)와 \(Y_i\)는 두 확률 변수의 관측값이고, \(\bar{X}\)와 \(\bar{Y}\)는 각각 두 확률 변수의 평균입니다. Python의 과학 컴퓨팅 관련 패키지를 사용하면 상관관계를 매우 편리하게 계산할 수 있습니다.

데이터 수집

이 기사에서는 바이낸스의 2023년 전체에 대한 4시간 K-라인 데이터를 수집하고, 1월 1일에 상장된 144개 암호화폐를 선정했습니다. 구체적인 다운로드 데이터 코드는 다음과 같습니다.

import requests
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

ticker = requests.get('https://fapi.binance.com/fapi/v1/ticker/24hr')
ticker = ticker.json()
sort_symbols = [k['symbol'][:-4] for k in sorted(ticker, key=lambda x :-float(x['quoteVolume'])) if k['symbol'][-4:] == 'USDT']

def GetKlines(symbol='BTCUSDT',start='2020-8-10',end='2023-8-10',period='1h',base='fapi',v = 'v1'):
    Klines = []
    start_time = int(time.mktime(datetime.strptime(start, "%Y-%m-%d").timetuple()))*1000 + 8*60*60*1000
    end_time =  min(int(time.mktime(datetime.strptime(end, "%Y-%m-%d").timetuple()))*1000 + 8*60*60*1000,time.time()*1000)
    intervel_map = {'m':60*1000,'h':60*60*1000,'d':24*60*60*1000}
    while start_time < end_time:
        time.sleep(0.5)
        mid_time = start_time+1000*int(period[:-1])*intervel_map[period[-1]]
        url = 'https://'+base+'.binance.com/'+base+'/'+v+'/klines?symbol=%s&interval=%s&startTime=%s&endTime=%s&limit=1000'%(symbol,period,start_time,mid_time)
        res = requests.get(url)
        res_list = res.json()
        if type(res_list) == list and len(res_list) > 0:
            start_time = res_list[-1][0]+int(period[:-1])*intervel_map[period[-1]]
            Klines += res_list
        if type(res_list) == list and len(res_list) == 0:
            start_time = start_time+1000*int(period[:-1])*intervel_map[period[-1]]
        if mid_time >= end_time:
            break
    df = pd.DataFrame(Klines,columns=['time','open','high','low','close','amount','end_time','volume','count','buy_amount','buy_volume','null']).astype('float')
    df.index = pd.to_datetime(df.time,unit='ms')
    return df

start_date = '2023-01-01'
end_date   = '2023-11-16'
period = '4h'
df_dict = {}

for symbol in sort_symbols:   
    print(symbol)
    df_s = GetKlines(symbol=symbol+'USDT',start=start_date,end=end_date,period=period)
    if not df_s.empty:
        df_dict[symbol] = df_s

df_close = pd.DataFrame(index=pd.date_range(start=start_date, end=end_date, freq=period),columns=df_dict.keys())
for symbol in symbols:
    df_s = df_dict[symbol]
    df_close[symbol] = df_s.close
df_close = df_close.dropna(how='any',axis=1)

시장 리뷰

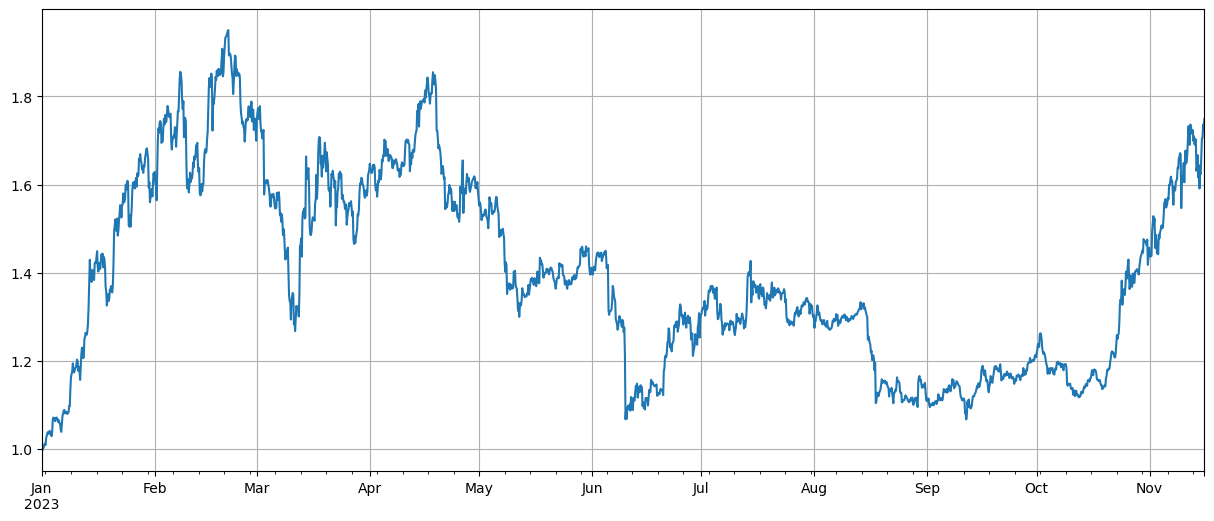
먼저, 데이터를 정규화한 후 평균 가격 상승 및 하락 지수를 계산했습니다. 2023년에는 두 가지 시장 상황이 있음을 알 수 있습니다. 하나는 연초에 크게 상승하는 것이고 다른 하나는 10월부터 크게 증가. 지수의 최고점.

df_norm = df_close/df_close.fillna(method='bfill').iloc[0] #归一化
total_index = df_norm.mean(axis=1)
total_index.plot(figsize=(15,6),grid=True);

상관관계 분석

판다에는 내장된 상관 관계 계산이 있습니다. BTC 가격과의 상관 관계는 아래 그림과 같습니다. 대부분의 통화는 양의 상관 관계를 가지고 있으며, 즉 BTC 가격을 따르는 반면, 일부 통화는 음의 상관 관계를 가지고 있습니다. 이는 디지털 화폐 시장의 변칙으로 여겨진다.

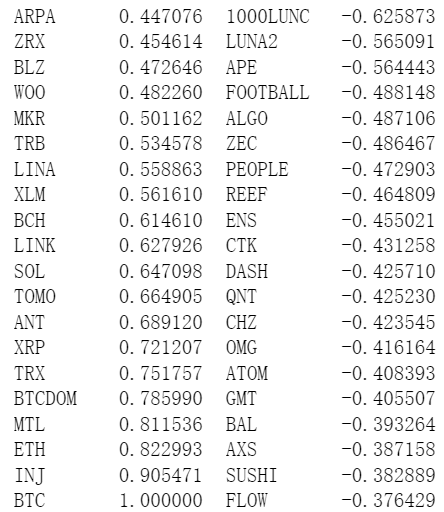
corr_symbols = df_norm.corrwith(df_norm.BTC).sort_values().index

상관관계와 가격 상승

여기서 우리는 통화를 두 그룹으로 느슨하게 나눕니다. 첫 번째 그룹은 BTC 가격과 가장 상관관계가 높은 40개 통화로 구성되고 두 번째 그룹은 BTC 가격과 가장 상관관계가 낮은 통화로 구성됩니다. 두 그룹의 지수는 평균 롱 포지션을 나타냅니다. 첫 번째 그룹의 포지션과 두 번째 그룹의 숏 포지션. 가격 변동과 BTC와의 상관관계를 계산할 수 있습니다. 코드와 결과는 다음과 같습니다.

(df_norm[corr_symbols[-40:]].mean(axis=1)-df_norm[corr_symbols[:40]].mean(axis=1)).plot(figsize=(15,6),grid=True);

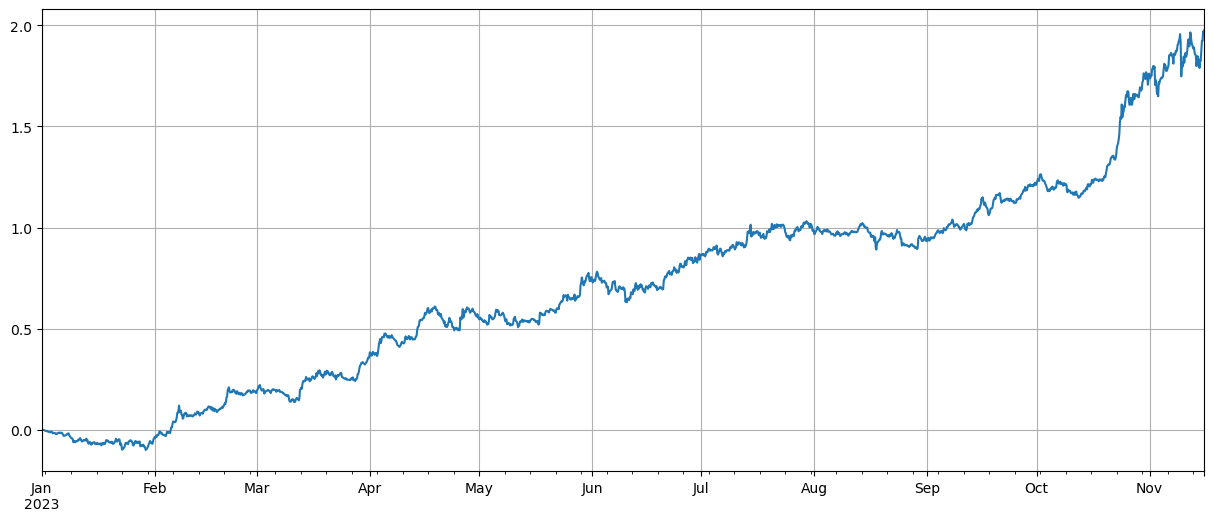
결과에 따르면, BTC 가격과 상관관계가 강한 통화일수록 성장이 더 좋으며, 상관관계가 낮은 통화를 매도하는 것도 좋은 헤지 역할을 합니다. 여기서 부정확한 부분은 미래 데이터를 사용하여 상관관계를 계산한다는 것입니다. 다음으로, 데이터는 두 그룹으로 나뉩니다. 하나는 상관관계를 계산하기 위한 것이고 다른 하나는 헤지 후 수익을 계산하기 위한 것입니다. 결과는 아래 그림에 나와 있습니다. 결론은 여전히 ​​같다.

시장 선두주자로서 비트코인과 이더리움의 가격 움직임은 종종 전체 시장에 큰 영향을 미칩니다. 비트코인 가격이 상승하면 시장 심리는 대체로 낙관적으로 변하고 많은 투자자가 시장 추세를 따르는 경향이 있습니다. 투자자들은 이를 전체 시장이 상승하고 있다는 신호로 보고 다른 통화를 매수하기 시작할 수도 있습니다. 주요 통화와 높은 상관관계를 갖는 코인은 시장 참여자들의 집단적 행동으로 인해 비슷한 가격 상승을 경험할 수 있습니다. 이 시점에서 가격 추세에 대한 시장의 예측은 때로는 스스로 실현되는 예언이 될 수 있습니다. 비트코인과 음의 상관관계를 가진 통화는 독특합니다. 기본이 악화되었거나 더 이상 주류 투자자의 시야에 들지 않을 수 있습니다. 심지어 비트코인에 대한 피를 빨아들이는 시장이 있을 수도 있습니다. 시장이 비트코인을 버렸습니다. 그들은 수익을 낼 수 있는 코인을 쫓아가세요.

corr_symbols = (df_norm.iloc[:1500].corrwith(df_norm.BTC.iloc[:1500])-df_norm.iloc[:1500].corrwith(total_index[:1500])).sort_values().index 

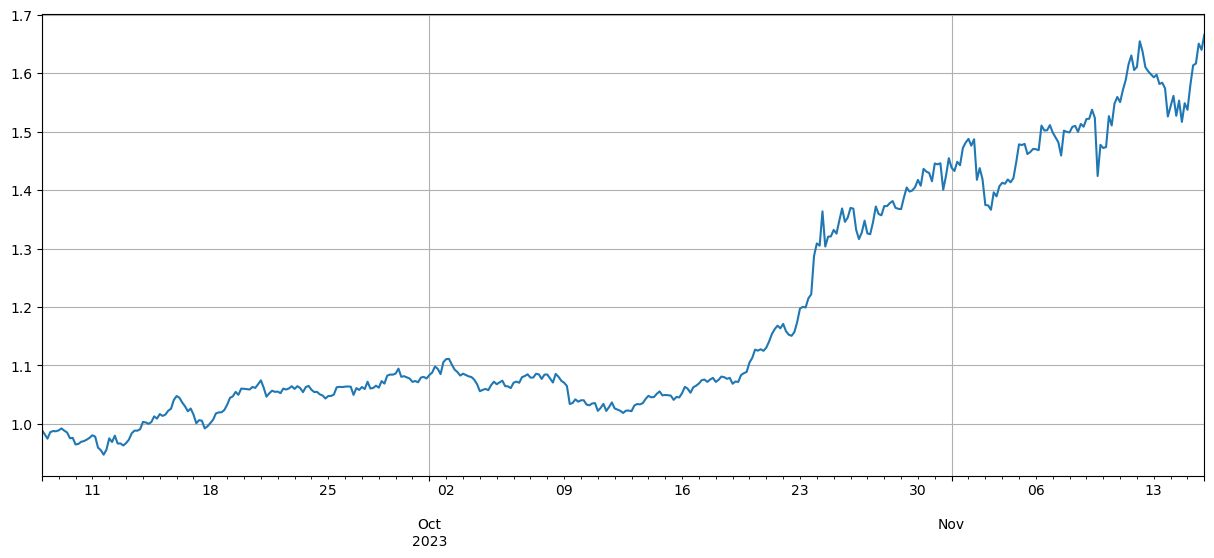
요약하다

이 논문에서는 피어슨 상관계수를 사용하여 통화 간의 상관관계의 정도를 밝혀냈습니다. 이 기사에서는 통화 간 상관관계를 계산하는 데 필요한 데이터를 얻고, 이 데이터를 사용하여 시장 동향을 평가하는 방법을 보여줍니다. 이는 디지털 화폐 시장의 가격 변동 동기화가 시장 심리와 전략을 반영하는 것일 뿐만 아니라 과학적 방법을 통해 정량화되고 예측될 수도 있음을 보여줍니다. 이는 특히 양적 거래 전략을 설계하는 데 중요합니다.

이 글에서 제시한 아이디어는 확장될 수 있는 부분이 많습니다. 예를 들어, 롤링 상관관계를 계산하거나, 증가와 감소 시의 상관관계를 별도로 계산하는 등, 정보를 더욱 효과적으로 분석하는 데 활용할 수 있습니다.