베이어스: 확률을 해독하는 비밀, 결정의 수학적인 지혜를 탐구하는 것

베이어스 통계학은 수학 분야의 강력한 대학 학문이며, 금융, 의학 연구, 정보 기술 등 많은 분야에서 광범위한 응용 분야가 있습니다. 이는 이전 신념을 증거와 결합하여 새로운 추후 신념을 도출하여 더 현명한 결정을 내릴 수 있도록 허용합니다.

이 기사에서는 이 분야를 창업한 주요 수학자들에 대해 간략하게 소개합니다.

베이스 이전 베이어스 통계를 더 잘 이해하기 위해서는 18세기에 다시 돌아가서 수학자 드 모이브레와 그의 논문?? 기회의 원리?? 를 참조해야 한다.[1]

그의 논문에서, 데 모이브레는 그의 시대의 확률과 도박과 관련된 많은 문제를 해결했다. 당신이 알고 있을 수 있듯이, 그의 문제 중 하나에 대한 해결책은 정규 분포의 기원에 이르렀지만 그것은 다른 이야기이다.

그의 논문에는 가장 간단한 질문이 있습니다.

은 공정한 동전을 3번 연속 던지며 3번의 긍정적인 확률을 얻습니다.

확률의 원칙에 대한 문제를 읽으면 대부분의 문제들이 하나의 가설로 시작하여 주어진 사건의 확률을 계산하는 것을 볼 수 있다. 예를 들어, 위의 문제에서, 동전이 공평하다고 가정하고 따라서 던지기에 긍정적 인 확률을 얻는 확률은 0.5이다.

오늘날 수학적으로 표현하면:

𝑃(𝑋|𝜃)

하지만 만약 우리가 이 동전이 공평한지 모른다면요?𝜃이봐요.

토마스 베이스와 리처드 프라이스

거의 50년 후인 1763년, 의 해결책 원칙에 대한 문제들에 대한 논문은 [2]이 런던의 로열 소사이어티의 철학 거래판에 발표되었다.

문서의 첫 몇 페이지에는 수학자 리처드 프라이스가 그의 친구 토마스 베이즈가 죽기 전 몇 년 전에 쓴 논문을 요약한 글이 있다. 소개에서 프라이스는 토마스 베이즈가 한 몇 가지 발견의 중요성을 설명하고 있다.

사실, 그는 특정 문제에 대해 언급했습니다.

은 알려지지 않은 사건의 발생과 실패의 수를 알고, 그 발생의 확률을 임의의 두 개의 이름의 확률 차원 사이에 있는 기회를 찾는다.

다른 말로 하면, 어떤 사건을 관찰한 후, 우리는 모르는 변수를 찾습니다.θ두 가지 확률 차원 사이의 확률은 얼마입니까? 이것은 실제로 역사에서 통계 추론과 관련된 첫 번째 문제 중 하나이며 역 확률이라는 이름을 얻었습니다. 수학 용어로:

𝑃( 𝜃 | 𝑋）

이것은 물론 오늘날 우리가 베이스 정리를 부르는 후속분포입니다.

원인은 없는 이유

이 두 장교를 알게 된 후,토마스 베이스그리고리처드 프라이스이 연구의 동기는 사실 매우 흥미롭습니다. 하지만 이를 위해 우리는 일시적으로 통계학에 대한 지식을 내려놓아야 합니다.

우리는 18세기에 살고 있으며 확률은 수학자들에 대한 관심의 영역이 되고 있다. 데모퍼나 베르누리 같은 수학자들에 의해 몇몇 사건들이 어느 정도 무작위로 발생하지만 여전히 고정된 규칙에 의해 지배된다는 것이 밝혀졌다. 예를 들어, 만약 당신이 여러 번 주사위를 던지면, 1/6의 시간이면 6에 머물게 된다. 이것은 마치 숨겨진 규칙이 기회의 운명을 결정하는 것과 같다.

이제, 여러분이 이 시대를 살아가는 수학자이자 신성한 신자라고 상상해보세요. 여러분은 숨겨진 법칙과 하나님과의 관계를 이해하는데 관심이 있을지도 모릅니다.

이것은 실제로 바이즈와 프라이스가 스스로 질문한 문제이다. 그들은 이 문제를 해결하기 위한 해결책을 직접적으로 적용하고자 하는데, 이는 세계가 지능과 지성의 결과일 수밖에 없다는 것을 증명하기 위한 것이다; 따라서 궁극적인 이유에 의해 신의 존재에 대한 증거를 제시하기 위한 것이다[2] - 즉, 인과없는 이유이다.

라프라스

놀랍게도, 약 2년 후인 1774년, 명백히 토마스 베이스의 논문을 읽지 않은 프랑스의 수학자 라프라스는 사건의 확률에 의해 사건의 이유를 파고드는 논문을 썼습니다.[3] 이것은 역 확률 문제에 관한 논문입니다. 첫 페이지에서 읽을 수 있습니다.

주요 원칙:

만약 하나의 사건이 n개의 다른 원인으로 인해 발생할 수 있다면, 주어진 사건의 이러한 원인들의 확률은 서로의 비율로 주어진 원인들의 사건의 확률과 같을 것이고, 이러한 원인들 각각의 존재 확률은 주어진 사건의 원인들의 확률과 같을 것이며, 주어진 이유들 중 각각의 사건의 확률의 합을 더한 것이다.

이것은 오늘날 우리가 알고 있는 바에이즈 정립입니다.

​

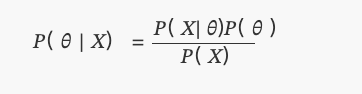
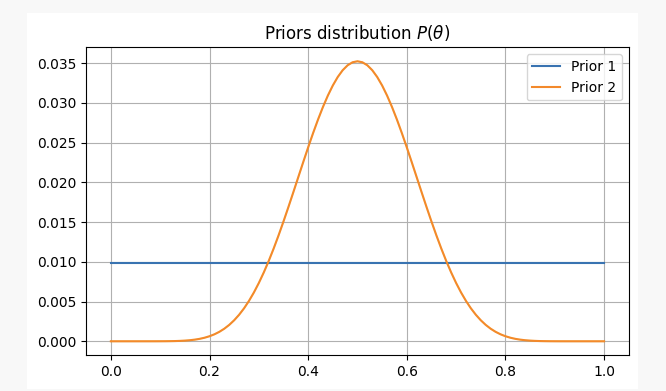
그 중P(θ)이 모든 것은 평평한 분포입니다.

동전 실험

우리는 파이썬과 PyMC 라이브러리를 사용하여 베이어스 통계를 현재로 가져와 간단한 실험을 할 것입니다.

만약 친구가 당신에게 동전을 주면, 그것이 공평한 동전이라고 생각하는지 물어봐요. 그가 시급하기 때문에, 그는 당신에게 10번만 동전을 던질 수 있다고 말합니다.p이 확률은 동전 던지기에 긍정적일 확률입니다p가장 가능성이 높은 값입니다.

(주의: 우리는 변수를 말하는 것이 아닙니다.p이 변수는 임의의 변수이고, 이 변수는 고정된 변수이고, 우리는 그것이 가장 가능성이 높은 값들 사이에서 있는지 알고 싶어한다.

이 문제에 대해 다른 시각을 가지기 위해 우리는 두 가지 다른 선입견을 가지고 문제를 해결합니다.

• 1, 동전의 공정성에 대한 사전 정보가 없으므로p이 경우 우리는 정보 없는 전자를 사용할 것입니다. 왜냐하면 당신은 당신의 신념에 정보를 추가하지 않았기 때문입니다.

• 두 번째, 경험으로 알고 있듯이, 동전이 불공평할 수도 있지만, 매우 불공평하게 만드는 것은 어렵습니다.p0.3보다 낮거나 0.7보다 높지 않을 가능성이 높습니다. 이 경우 우리는 정보 전자를 사용할 것입니다.

이 두 가지 경우에 대한 우리의 사전 믿음은 다음과 같습니다.

동전을 10번 던지면 두번 긍정적인 결과를 얻습니다.p？

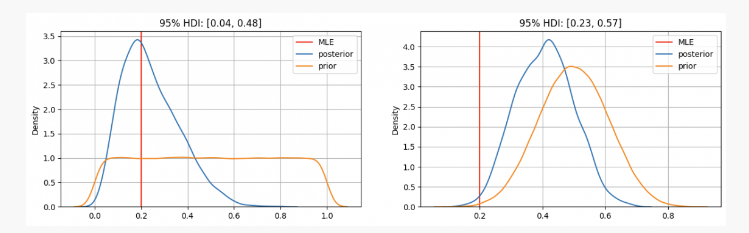
이 경우, 이 경우, 이 경우,p전후 분포는 최대 유사 추정치 (MLE) 에 집중됩니다.p=0.2, 이는 주파수 학파 방법을 사용하는 것과 유사한 방법이다. 진실된 알 수없는 매개 변수는 0.04과 0.48 사이의 95% 신뢰 범위 내에 위치할 것이다.

다른 한편으로, 높은 신뢰도와 함께p0.3과 0.7 사이의 경우, 우리는 후속값 분포가 0.4 정도라고 볼 수 있으며, 이는 우리의 MLE가 제공하는 값보다 훨씬 높습니다. 이 경우, 진정한 미지의 매개 변수는 95%의 신뢰 범위 안에 있고, 0.23과 0.57 사이에 있습니다.

따라서, 첫 번째 경우, 당신은 당신의 친구에게 당신이 이 동전이 공정하지 않다고 확신한다고 말할 것입니다. 그러나 다른 경우, 당신은 당신에게 이 동전이 공정인지 확신할 수 없다고 말할 것입니다.

당신이 볼 수 있듯이, 같은 증거가 있는 상황에서도 (10번의 투사 중 2번은 긍정적으로) 다른 전제적 신념 아래에서 결과가 달라질 수 있다. 이것은 바이에스 통계학의 장점이며, 과학적 방법과 유사하게, 그것은 우리가 전제적 신념을 새로운 관찰과 증거와 결합하여 우리의 신념을 갱신할 수 있도록 허용한다.

END

오늘 기사에서는 베이어스 통계학의 기원과 그 주요 기여자를 살펴볼 것입니다. 그 후에도 이 분야에 많은 다른 중요한 기여자들이 (제프레이스, 콕스, 샤논 등) 존재했습니다.转载自quantdare.com。