FMEX 정렬은 최적의 주문 수량 최적화를 실현합니다.
 0
0
 2177
2177

FMEX의 붕괴는 많은 사람들에게 큰 어려움을 줬지만, 최근에 재시작 계획을 내놓고 원래 채굴과 유사한 규칙을 제정해 부채를 탕감했습니다. 거래 마이닝에 대한 분석 기사가 제공되었습니다: https://www.fmz.com/bbs-topic/5834. 정렬 채굴에도 최적화의 여지가 있습니다. 사람들은 같은 구덩이에 두 번 빠져서는 안 되지만, FMEX에 대한 청구권이 있는 사람들은 그것을 참조하고 싶어할 수 있습니다. FMZ 정량적 플랫폼에서 실행할 수 있는 구체적인 실시간 전략도 공개될 수 있습니다.
FMEX 정렬 잠금 해제 규칙
매일 5분을 정렬 잠금 해제 주기로 정의하고, 각 주기에는 그날 거래 쌍의 정렬 잠금 해제 할당량의 1/288이 할당됩니다. 각 사이클에서 거래 쌍의 매수 및 매도 주문의 스냅샷을 찍기 위해 무작위 시간 지점이 선택됩니다. 여기서:
- 구매 1 유저 주문금액 비중에 따라 잠금해제 기간의 반환금액의 1/4이 이 랭킹에 할당됩니다.
- 판매 1 유저 주문금액 비중에 따라 잠금해제 기간의 반환금액의 1/4이 이 랭킹에 할당됩니다.
- 2개 구매~5개 구매의 4단계에 대해, 잠금 해제 기간의 반환 금액의 1/40이 각 단계에서 사용자의 주문 금액 비중에 따라 할당됩니다.
- 매도2~매도5 4단계 주문에 대해서는, 각 단계의 사용자 주문금액 비중에 따라 랭킹 잠금해제 기간의 반환금액의 1/40이 할당됩니다.
- 매수 6에서 매수 10까지 5개 주문에 대해 잠금 해제 기간의 반환 금액의 1/50이 각 주문에서 주문 금액의 비중에 따라 할당됩니다.
- 6~10까지의 5개 주문에 대해서는 잠금 해제 기간의 반환 금액의 1/50이 각 주문에서 주문 금액이 차지하는 비율에 따라 각 주문에 할당됩니다.
- 매수 11에서 매수 15까지의 5개 주문에 대해 잠금 해제 기간의 반환 금액의 1/100이 각 주문에서 주문 금액의 비중에 따라 각 주문에 할당됩니다.
- 매도 11호부터 매도 15호까지의 5개 주문에 대해 잠금 해제 기간의 반환 금액의 1/100이 각 주문의 주문 금액 비중에 따라 각 주문에 할당됩니다.
같은 날 특정 거래 쌍에 대한 사용자의 순위 잠금 해제로 인한 총 수익은 거래 쌍의 각 주기에서 순위 잠금 해제로 인해 사용자에게 반환된 금액의 합계입니다.
혜택을 잠금 해제하기 위한 정렬
첫째, 정렬 및 잠금 해제의 총 수입은 다음과 같습니다.
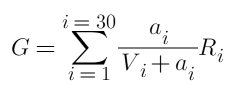
여기서 i는 포지션 중 하나를 나타내며, 양 당사자 모두 총 30개의 포지션이 있습니다. a는 보류 중인 주문 수량, R은 잠금 해제 반환 금액, V는 기존 주문의 총 수입니다.
거래 잠금 해제와 달리 주문을 하는 데는 비용이 없습니다. 여기서 R은 상대적인 크기만 고려하면 되고 USDT로 표시된 절대 금액은 고려할 필요가 없습니다. 보류 중인 주문의 총 수를 결정하면, 문제는 이익 G를 극대화하기 위해 주문을 다양한 포지션에 어떻게 할당할 것인가가 됩니다. 단순히 주문 수량이 가장 적은 위치를 찾아 모든 주문을 거기에 하는 것은 분명히 최적의 해결책이 아닙니다. 예를 들어, 10개의 기존 주문이 있는 3개의 포지션이 있고, 그들의 R은 동일합니다. 우리는 총 주문량을 30으로 설정합니다. 주문을 하기 위해 하나의 포지션만 선택하면 최종 총 이익은 0.75R입니다. 10, 최종 이익은 1.5R인데, 이는 때로는 분산 주문의 이익이 더 좋다는 것을 보여줍니다. 그러면 자금을 어떻게 배분하시나요?
정렬 잠금 해제 최적화
마지막으로, 최적화 목표와 제약 사항은 다음과 같습니다.
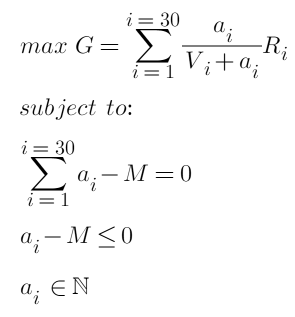
여기서 M은 총 주문 수량입니다. 이것은 부등식을 포함하는 이차 볼록 최적화 문제로, KTT 조건을 만족하고 정수 해를 가집니다. 해당 패키지와 볼록 최적화 솔버를 사용하면 결과를 직접 얻고 각 포지션에 대한 최적의 주문 수량을 반환할 수 있어야 합니다. 하지만 이것은 분명히 우리가 원하는 답이 아닙니다. 우리는 문제를 단순화하고 구체적인 해결책 단계를 얻어야 합니다.
간단한 예로 시작해 보겠습니다.
두 계층만 고려합니다. 현재 주문량은 10과 20입니다(각각 1계층과 2계층이라고 함). 잠금 해제 할당량은 모두 R입니다. 전략 예비 주문의 총 수는 30입니다. 어떻게 할당해야 합니까? 자금 잠금 해제 한도가 최대화되었습니까? 이 질문은 간단해 보이지만 계산 없이 올바른 결론을 내리기는 어렵습니다. 독자는 먼저 스스로 답을 생각해 보는 것이 좋습니다.
시나리오 1:
최소 주문 위치를 찾고 거기에 모든 주문을 하면 총 이익은 G=30/(30+10)=0.75R이 됩니다. 이것은 생각해 볼 수 있는 가장 쉬운 해결책이기도 합니다.
시나리오 2:
1위안은 매번 할당되며, 가장 큰 수익을 낼 수 있는 곳, 즉 보류 주문 수가 가장 적은 곳에 할당됩니다. 그러면 첫 번째 위안은 첫 번째 계층에 할당되고, 첫 번째 계층의 주문량은 10+1이 됩니다. 두 번째 위안도 첫 번째 계층에 할당되고… 이런 식으로 총 10 위안이 될 때까지 계속됩니다. 1단계에 할당됩니다. 이때, 1개가 무작위로 선택되고, 1단계의 보류 주문 총 수가 20개를 초과하면 2단계에 할당됩니다. 최종 결과는 1차에 20위안, 2차에 10위안이 할당되어, 두 회사의 최종 주문은 모두 30입니다. 총 이익 G=20⁄30+10⁄30=R. 이 해결책은 해결책 1보다 훨씬 뛰어나고, 계산하기도 더 쉽습니다.
해결책 3:
첫 번째 계층은 a가 할당되고 두 번째 계층은 30-a라고 가정할 수 있습니다. 그런 다음 방정식을 직접 나열하고 그 미분을 0으로 찾을 수 있습니다(여기에는 프로세스가 나열되지 않으며 거래 잠금 해제에 대한 기사와 유사합니다). ), 최종 결과를 계산합니다. 공식은 다음과 같습니다.
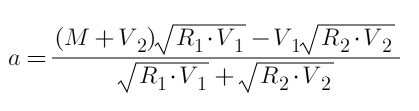
정수를 대입하면 a=15가 됩니다. 총 이익 G=15⁄25+15⁄35=1.0286R, 이는 옵션 2보다 더 좋습니다. 이는 공식에서 직접 도출되었으므로 최적의 솔루션입니다. 독자는 확인할 수 있습니다.
결과는 예상과 다를 수 있습니다. Plan 2의 각 달러 할당이 현재 상황에서 최적의 솔루션이라는 것은 분명합니다. 전체적으로 최적의 솔루션이 아닌 이유는 무엇입니까? 이런 상황은 매우 흔합니다. 지역적 최적은 반드시 전체적 최적은 아닙니다. 왜냐하면 할당 전에 주문은 이미 자금을 투자했고, 전체적 효율성은 침몰 비용을 고려해야 하기 때문입니다. 최적화의 각 단계에서 우리의 목표는 단일한 이점을 극대화하는 것이 아니라 전반적인 효율성을 극대화하는 것입니다.
특정 최적화 계획
마침내 우리는 실제로 실행 가능한 작업을 시작했습니다. 매번 1위안을 할당하여 문제를 단순화해 보겠습니다. 먼저 효율성을 측정해 보겠습니다. 파생 상품은 G에 대한 각 a의 기여도를 반영할 수 있습니다. 이 기여도는 단일 분포의 이익보다는 누적 비용을 고려합니다. 값이 클수록 최종 이익에 대한 전반적인 기여도가 커집니다. . 분명히 함수의 그래프에 따르면 a=1일 때 존재에서 비존재로 효율성이 가장 높고, 그 이후로는 점차 감소합니다.
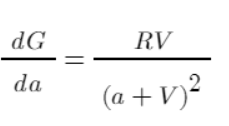
위의 간단한 예를 예로 들면, 우리는 자금 배분의 효율성을 계산하고 이를 표로 나열할 수 있습니다.
| 자금 | 1 | 2 |
|---|---|---|
| 1 | 0.0826 | 0.0454 |
| 2 | 0.069 | 0.0413 |
| 3 | 0.0592 | 0.0378 |
| 4 | 0.051 | 0.0347 |
| 5 | 0.0444 | 0.032 |
| … | … | … |
|12 | 0.0207 |0.0195| |13 | 0.0189 |0.0184| |14 | 0.0174 |0.0173| |15 | 0.016 |0.0163| |16 | 0.0148 |0.0154| |17 | 0.0137 |0.0146| |18 | 0.0128 |0.0139|
표에 따르면 1위안은 1등급에 배정되고, 2위안은 1등급에 배정되고… 5위안은 2등급에 배정되고… 이런 식으로 계속되어 최종적으로 15위안이 배정됩니다. 첫 번째 계층은 15위안이고 두 번째 계층은 15위안입니다. 위안은 방정식에 근거하여 계산한 최적의 솔루션입니다. 특히 30단 기어의 경우 알고리즘은 동일하며 구체적인 단계는 다음과 같습니다.
- 1. 먼저 모든 기어를 확인합니다. V=0이면 a=1이고 더 이상 자금이 할당되지 않습니다.
- 2. 전체 자금을 N개 부분으로 분배하고, 매번 분배할 기어를 선택합니다.
- 3. 각 기어의 효율성을 계산합니다 = RV/pow(a+V,2), 여기서 a는 해당 포지션에 할당된 누적 자금 + 이번에 할당된 자금을 나타냅니다.
- 4. 가장 효율적인 장비에 자금을 할당하고, 효율성이 같으면 무작위로 하나를 선택합니다.
- 5. 자금이 할당될 때까지 3-4를 반복합니다.
총 주문량이 많으면 한 번에 각 달러를 할당하는 것은 너무 비효율적입니다. 자금을 100개 부분으로 나누고 한 번에 한 부분씩 할당할 수 있습니다. 간단한 계산과 정렬이기 때문에 알고리즘은 매우 효율적인. 구체적으로 실행 수준에서는 여전히 최적화의 여지가 있는데, 예를 들어 주문을 100개로 나누어 매번 조정할 때 모든 주문을 취소하는 대신 주문만 재할당하면 되도록 하는 것입니다. R 값을 직접 설정하고 시장에서 멀리 떨어진 사람들에게 더 많은 가중치를 줄 수도 있습니다. 정렬 잠금 해제와 보류 주문 잠금 해제 사이에 중복이 있는 경우, 둘을 함께 고려할 수 있습니다.
이 기사는 FMZ Quantitative Platform의 원본 기사입니다. 전송할 때 출처를 표시하세요: https://www.fmz.com/bbs-topic-new/5843