리소스 로딩... 로딩...
  1. 소화
  2. 토론
  3. 데이터 기반 기술에 기반한 쌍 거래

데이터 기반 기술에 기반한 쌍 거래

저자:FMZ~리디아, 창작: 2023-01-05 09:10:25, 업데이트: 2024-12-19 00:27:10

img

데이터 기반 기술에 기반한 쌍 거래

페어 트레이딩은 수학적 분석에 기반한 트레이딩 전략을 수립하는 좋은 예입니다. 이 기사에서는 페어 트레이딩 전략을 만들고 자동화하는 데 데이터를 사용하는 방법을 보여줍니다.

기본 원칙

예를 들어, 두 회사가 같은 제품을 생산하는 경우, 예를 들어 펩시콜라와 코카콜라가 같은 제품을 생산하는 경우, 두 회사의 가격 비율 또는 기본 스프레드 (가격 차이로도 알려져 있습니다) 가 시간이 지남에 따라 변하지 않도록 유지되기를 바랍니다. 그러나, 투자 목표의 큰 구매/판매 주문과 회사의 중요한 소식에 대한 반응과 같은 수요와 공급의 일시적인 변화로 인해 두 쌍 사이의 가격 차이는 시간이 지남에 따라 다를 수 있습니다. 이 경우, 한 투자 대상은 서로 상대적으로 상승하고 다른 하나는 감소합니다. 이 불협의가 시간이 지남에 따라 정상으로 돌아가는 것을 원한다면, 거래 기회 (또는 중재 기회) 를 찾을 수 있습니다. 이러한 중재 기회는 디지털 통화 시장이나 국내 상품 선물 시장에서 어디에서나 찾을 수 있습니다. 예를 들어 BTC와 안전 하번 자산의 관계에 대한 관계; 소아 쌀, 소아 기름과 소아 쌀의 미래에셋 품종.

일시적인 가격차가 있을 때, 당신은 뛰어난 성능의 투자 대상을 판매하고 낮은 성능의 투자 대상을 구매할 것이다. 당신은 두 투자 대상의 이익 마진이 결국 뛰어난 성능의 투자 대상의 하락이나 낮은 성능의 투자 대상의 상승 또는 둘 다로 떨어질 것이라고 확신한다. 당신의 거래는 이러한 모든 비슷한 상황에서 돈을 벌 것이다. 만약 투자 대상이 서로 사이의 가격 차이를 변화시키지 않고 함께 상승하거나 하락한다면, 당신은 돈을 벌거나 잃지 않을 것이다.

따라서 쌍 거래는 시장 중립적인 거래 전략으로 거래자가 거의 모든 시장 조건에서 이익을 얻을 수 있습니다. 상승 추세, 하락 추세 또는 수평 통합.

개념 설명: 두 가상의 투자 목표

  • FMZ 퀀트 플랫폼에 우리의 연구 환경을 구축

우선, 원활한 작업을 위해, 우리는 우리의 연구 환경을 구축해야합니다. 이 기사에서는 FMZ 퀀트 플랫폼을 사용합니다 (FMZ.COM) 를 구축하기 위해 연구 환경을 구축했습니다. 주로 편리하고 빠른 API 인터페이스와 이 플랫폼의 잘 포장된 Docker 시스템을 나중에 사용할 수 있습니다.

FMZ 퀀트 플랫폼의 공식 명칭에서 이 도커 시스템은 도커 시스템이라고 불린다.

도커와 로봇을 어떻게 배포해야 하는지에 대한 제 이전 기사를 참조하시기 바랍니다:https://www.fmz.com/bbs-topic/9864.

독자들이 자신의 클라우드 컴퓨팅 서버를 구입하여 도커를 배포하고 싶다면 이 기사를 참조할 수 있습니다.https://www.fmz.com/digest-topic/5711.

클라우드 컴퓨팅 서버와 도커 시스템을 성공적으로 배포한 후, 다음으로 우리는 파이썬의 현재 가장 큰 유물을 설치합니다: 아나콘다

이 문서에서 요구되는 모든 관련 프로그램 환경 ( 의존성 라이브러리, 버전 관리 등) 을 구현하기 위해 가장 간단한 방법은 아나콘다를 사용하는 것입니다. 그것은 패키지 된 파이썬 데이터 과학 생태계 및 의존성 라이브러리 관리자입니다.

아나콘다의 설치 방법에 대해서는 아나콘다의 공식 가이드를 참조하십시오.https://www.anaconda.com/distribution/.

이 문서에서는 또한 파이썬 과학 컴퓨팅에서 두 가지 인기 있고 중요한 라이브러리인 numpy와 panda를 사용할 것입니다.

위의 기본 작업은 아나콘다 환경 및 피 및 판다 라이브러리를 설정하는 방법에 대해 소개하는 이전 기사를 참조 할 수 있습니다. 자세한 내용은 참조하십시오:https://www.fmz.com/bbs-topic/9863.

다음으로, 두 가지 가상의 투자 목표를 구현하기 위해 코드를 사용해보자:

import numpy as np
import pandas as pd

import statsmodels
from statsmodels.tsa.stattools import coint
# just set the seed for the random number generator
np.random.seed(107)

import matplotlib.pyplot as plt

네, 우리는 또한 matplotlib을 사용할 것입니다. 파이썬에서 매우 유명한 차트 라이브러리입니다.

가설적인 투자 목표 X를 생성하고 정상적인 분포를 통해 일일 수익을 시뮬레이션하고 그래프화합니다. 그러면 우리는 일일 X 값을 얻기 위해 누적 합을 수행합니다.

# Generate daily returns
Xreturns = np.random.normal(0, 1, 100) 
# sum them and shift all the prices up
X = pd.Series(np.cumsum(
    Xreturns), name='X') 
    + 50
X.plot(figsize=(15,7))
plt.show()

img

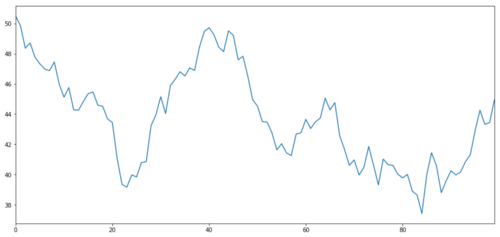
투자 대상의 X는 정상적인 분포를 통해 일일 수익을 그리기 위해 시뮬레이션됩니다.

이제 우리는 Y를 생성합니다. Y가 X와 밀접하게 통합되어 있기 때문에 Y의 값은 X의 변화와 매우 비슷해야 합니다. 우리는 X를 가져다가

noise = np.random.normal(0, 1, 100)
Y = X + 5 + noise
Y.name = 'Y'
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.show()

img

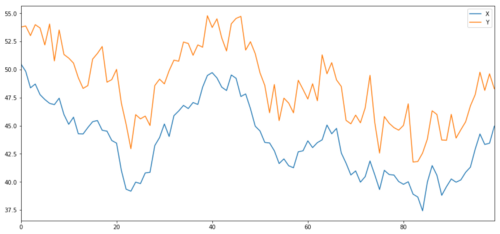
코인테그레이션 투자 대상의 X와 Y

통합

공분화는 상관관계에 매우 유사하므로 두 데이터 시리즈 사이의 비율이 평균 값에 가깝게 변한다는 것을 의미합니다. Y와 X 시리즈는 다음과 같습니다.

Y = X + e

여기서 은 일정한 비율이고 e는 소음입니다.

두 개의 시간 계열 사이에 거래하는 쌍의 경우, 시간의 흐름에 따라 비율의 예상 값은 평균 값에 동원되어야 합니다. 즉, 그들은 공동 통합되어야 합니다. 위에서 만든 시간 계열은 공동 통합됩니다. 이제 그 사이의 비율을 그래프화하여 그것이 어떻게 보이는지 볼 수 있습니다.

(Y/X).plot(figsize=(15,7)) 
plt.axhline((Y/X).mean(), color='red', linestyle='--') 
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()

img

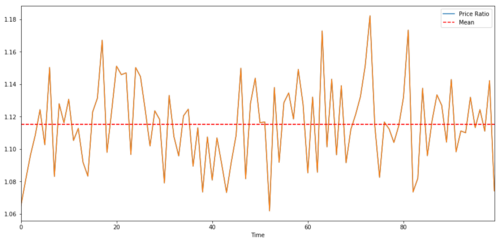
두 개의 통합된 투자 목표 가격의 비율과 평균 값

동결합 테스트

편리한 테스트 방법은 statsmodels.tsa.stattools를 사용하는 것입니다. 우리는 가능한 한 공동 통합 된 두 개의 데이터 시리즈를 인위적으로 생성했기 때문에 매우 낮은 p 값을 볼 수 있습니다.

# compute the p-value of the cointegration test
# will inform us as to whether the ratio between the 2 timeseries is stationary
# around its mean
score, pvalue, _ = coint(X,Y)
print pvalue

결과는 1.81864477307e-17입니다.

참고: 상관관계 및 공동 통합

상관관계와 공동 통합은 이론적으로 비슷하지만 같은 것은 아닙니다. 관련하지만 공동 통합되지 않은 데이터 시리즈의 예를 보겠습니다. 그리고 반대로. 먼저, 방금 생성한 일련의 상관관계를 확인해보겠습니다.

X.corr(Y)

결과는: 0.951

우리가 예상했듯이, 이것은 매우 높습니다. 하지만 서로 연관되어 있지만 공동 통합되지 않은 두 개의 시리즈는 어떨까요? 간단한 예로는 두 개의 오차 데이터의 일련입니다.

ret1 = np.random.normal(1, 1, 100)
ret2 = np.random.normal(2, 1, 100)

s1 = pd.Series( np.cumsum(ret1), name='X')
s2 = pd.Series( np.cumsum(ret2), name='Y')

pd.concat([s1, s2], axis=1 ).plot(figsize=(15,7))
plt.show()
print 'Correlation: ' + str(X_diverging.corr(Y_diverging))
score, pvalue, _ = coint(X_diverging,Y_diverging)
print 'Cointegration test p-value: ' + str(pvalue)

img

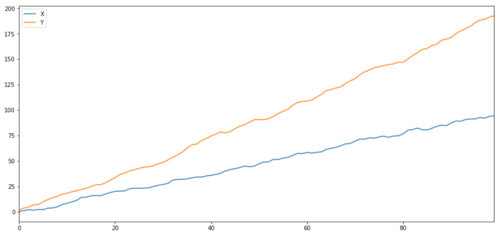
두 개의 관련 시리즈 (함께 통합되지 않은)

상관률: 0.998 P 값: 0.258

상관관계가 없는 공동합성의 간단한 예는 정상적인 분포 염기서열과 제곱파이다.

Y2 = pd.Series(np.random.normal(0, 1, 800), name='Y2') + 20
Y3 = Y2.copy()
Y3[0:100] = 30

Y3[100:200] = 10
Y3[200:300] = 30
Y3[300:400] = 10
Y3[400:500] = 30
Y3[500:600] = 10
Y3[600:700] = 30
Y3[700:800] = 10
Y2.plot(figsize=(15,7))
Y3.plot()
plt.ylim([0, 40])
plt.show()
# correlation is nearly zero
print 'Correlation: ' + str(Y2.corr(Y3))
score, pvalue, _ = coint(Y2,Y3)
print 'Cointegration test p-value: ' + str(pvalue)

img

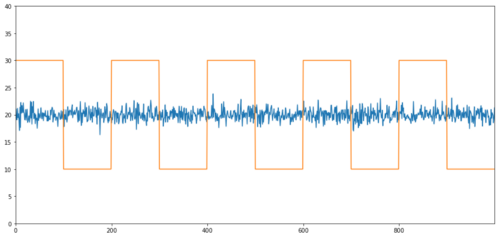
상관관계: 0.007546 P 값: 0.0

상관관계는 매우 낮지만, p값은 완벽한 통합을 보여줍니다!

쌍 거래는 어떻게 해야 할까요?

두 개의 공동 통합된 시간 계열 (위와 같은 X 및 Y) 이 서로 마주보고 서로 벗어나기 때문에 때로는 기본 스프레드가 높거나 낮습니다. 우리는 한 가지 투자 대상을 구입하고 다른 것을 판매함으로써 쌍 거래를 수행합니다. 이렇게 두 가지 투자 목표가 함께 떨어지거나 상승하면 돈을 벌거나 돈을 잃지 않습니다. 즉, 우리는 시장에서 중립적입니다.

위와 같이, X와 Y의 Y = X + e, 그래서 비율 (Y/X) 는 평균 값 주위를 움직입니다. 우리는 평균 값 반전의 비율을 통해 돈을 벌습니다. 이를 위해 X와 Y가 멀리 떨어져있는 경우, 즉 의 값이 너무 높거나 너무 낮다는 경우에 주의를 기울일 것입니다.

  • 긴 비율: 이것은 비율이 매우 작고 증가할 것으로 예상되는 경우입니다. 위의 예제에서, 우리는 긴 Y로 이동하고 짧은 X로 포지션을 개척합니다.

  • 짧은 비율: 이것은 비율이 매우 크고 감소할 것으로 예상되는 경우입니다. 위의 예제에서 우리는 Y를 짧게하고 X를 길게하여 포지션을 개척합니다.

우리는 항상 '헤지 포지션'을 가지고 있다는 것을 유의하십시오. 거래 대상이 손실 가치를 구입하면 짧은 포지션은 돈을 벌고 반대로, 그래서 우리는 전체 시장 추세에 면역됩니다.

만약 거래 대상의 X와 Y가 서로 상대적으로 움직이면 우리는 돈을 벌거나 돈을 잃게 됩니다.

비슷한 동작을 가진 거래 대상을 찾기 위해 데이터를 사용

가장 좋은 방법은 협동 통합이 될 수 있다고 의심하는 거래 대상에서 시작하여 통계 테스트를 수행하는 것입니다. 모든 거래 쌍에 통계 테스트를 수행하면다중 비교 편향.

다중 비교 편향많은 테스트를 실행할 때 중요한 p값을 잘못 생성할 확률이 증가하기 때문에 많은 수의 테스트를 실행해야 합니다. 무작위 데이터에 100개의 테스트를 실행하면 0.05 이하의 5p값을 볼 수 있습니다. n (n-1)/2의 비교를 수행하면 많은 잘못된 p값을 볼 수 있습니다. 이 상황을 피하기 위해 몇 개의 거래 쌍을 선택하고 그들이 코인테그레이션이 될 수 있음을 결정하고 개별적으로 테스트하십시오. 이것은 크게 감소합니다.다중 비교 편향.

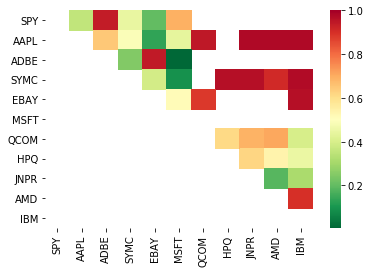
따라서, 협동 통합을 보여주는 몇 가지 거래 목표를 찾으려고 하자. 예를 들어 S&P 500 지수에서 큰 미국 기술 주식의 바구니를 보자. 이러한 거래 목표는 유사한 시장 부문에서 운영되며 협동 통합 가격을 가지고 있습니다. 우리는 거래 객체의 목록을 스캔하고 모든 쌍 사이의 협동 통합을 테스트합니다.

복귀된 코인테그레이션 테스트 스코어 매트릭스, p값 매트릭스 및 p값이 0.05보다 작은 모든 쌍이 방법은 복수의 비교 편견에 취약하기 때문에 실제로 두 번째 검사를 수행해야 합니다.이 기사 에서는 설명 을 편리 하게 하기 위해 이 예 에서 이 점 을 무시 하기 를 택 합니다.

def find_cointegrated_pairs(data):
    n = data.shape[1]
    score_matrix = np.zeros((n, n))
    pvalue_matrix = np.ones((n, n))
    keys = data.keys()
    pairs = []
    for i in range(n):
        for j in range(i+1, n):
            S1 = data[keys[i]]
            S2 = data[keys[j]]
            result = coint(S1, S2)
            score = result[0]
            pvalue = result[1]
            score_matrix[i, j] = score
            pvalue_matrix[i, j] = pvalue
            if pvalue < 0.02:
                pairs.append((keys[i], keys[j]))
    return score_matrix, pvalue_matrix, pairs

참고: 우리는 시장 벤치마크 (SPX) 를 데이터에 포함했습니다. 시장은 많은 거래 대상의 흐름을 주도했습니다. 일반적으로 결합 된 것처럼 보이는 두 개의 거래 대상을 찾을 수 있습니다. 그러나 실제로는 서로 통합되지 않고 시장과 결합합니다. 이것은 혼란 변수라고합니다. 당신이 발견하는 모든 관계에서 시장 참여를 확인하는 것이 중요합니다.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2007/12/01'
endDateStr = '2017/12/01'
cachedFolderName = 'yahooData/'
dataSetId = 'testPairsTrading'
instrumentIds = ['SPY','AAPL','ADBE','SYMC','EBAY','MSFT','QCOM',
                 'HPQ','JNPR','AMD','IBM']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
data = ds.getBookDataByFeature()['Adj Close']
data.head(3)

img

이제 우리의 방법을 사용하여 통합된 거래 쌍을 찾으려고 노력하겠습니다.

# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds, 
                yticklabels=instrumentIds, cmap=’RdYlGn_r’, 
                mask = (pvalues >= 0.98))
plt.show()
print pairs

[('ADBE', 'MSFT')]

img

ADBE과 MSFT이 통합된 것 같습니다. 가격을 살펴보면 정말 의미가 있는지 확인해 볼 수 있습니다.

S1 = data['ADBE']
S2 = data['MSFT']
score, pvalue, _ = coint(S1, S2)
print(pvalue)
ratios = S1 / S2
ratios.plot()
plt.axhline(ratios.mean())
plt.legend([' Ratio'])
plt.show()

img

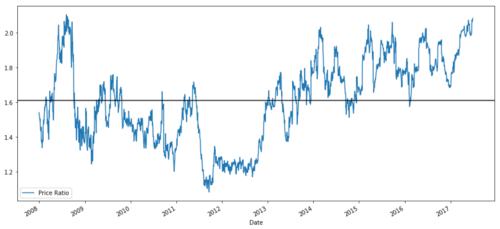
2008년부터 2017년까지 MSFT와 ADBE의 가격비율 차트

이 비율은 안정적인 평균처럼 보입니다. 절대 비율은 통계적으로 유용하지 않습니다. Z 점수로 취급함으로써 신호를 표준화하는 것이 더 유용합니다. Z 점수는 다음과 같이 정의됩니다.

Z 점수 (값) = (값 평균) / 표준편차

경고

사실, 우리는 일반적으로 데이터가 정상적으로 분포되어 있다는 전제에서 데이터를 확장하려고 노력합니다. 그러나 많은 금융 데이터가 정상적으로 분포되어 있지 않으므로 통계를 생성 할 때 정상성이나 특정 분포를 단순히 가정하지 않도록 매우 조심해야합니다. 비율의 진정한 분포는 지방 꼬리 효과를 가질 수 있으며 극단적인 경향이있는 데이터는 모델을 혼란스럽게하고 엄청난 손실을 초래합니다.

def zscore(series):
    return (series - series.mean()) / np.std(series)

zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()

img

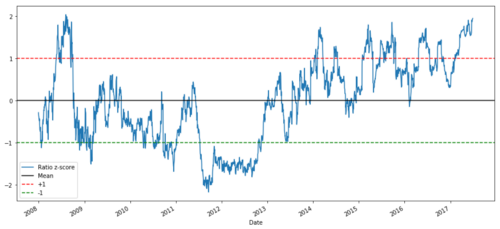
2008년부터 2017년까지 MSFT와 ADBE 사이의 Z 가격 비율

이제 평균값에 가까운 비율의 움직임을 더 쉽게 관찰할 수 있습니다. 하지만 때로는 평균값과 큰 차이를 쉽게 볼 수 있습니다. 이것을 활용할 수 있습니다.

이제 우리는 쌍 거래 전략의 기본 지식을 논의하고 역사적 가격에 따라 공동 통합의 주제를 결정 한 후에 거래 신호를 개발하려고 노력하겠습니다. 먼저 데이터 기술을 사용하여 거래 신호를 개발하는 단계를 검토해 보겠습니다.

  • 신뢰성 있는 데이터를 수집하고 데이터를 정화합니다.

  • 거래 신호/논리를 식별하기 위해 데이터에서 함수를 생성합니다.

  • 함수는 이동 평균 또는 가격 데이터, 상관관계 또는 더 복잡한 신호의 비율이 될 수 있습니다. 새로운 함수를 만들기 위해 결합하십시오.

  • 이 함수를 사용하여 거래 신호를 생성합니다. 즉 어떤 신호가 구매, 판매 또는 쇼트 포지션인지 관찰합니다.

다행히 FMZ Quant 플랫폼이 있습니다 (fmz.com), 이는 우리에게 위 네 가지 측면을 완성시켰고, 이는 전략 개발자들에게 큰 축복입니다. 우리는 우리의 에너지와 시간을 전략 논리 설계와 기능 확장에 할애 할 수 있습니다.

FMZ 퀀트 플랫폼에는 다양한 주류 거래소에 대한 캡슐화된 인터페이스가 있습니다. 우리가 해야 할 일은 이러한 API 인터페이스를 호출하는 것입니다. 기본 구현 논리의 나머지 부분은 전문 팀에 의해 완료되었습니다.

논리를 완성하고 원리를 설명하기 위해 이 문서에서는 이러한 기본 논리를 상세히 소개할 것입니다. 그러나 실제 동작에서 독자들은 위의 네 가지 측면을 완료하기 위해 FMZ Quant API 인터페이스를 직접 호출할 수 있습니다.

시작하자:

1단계: 질문 을 설정 하십시오

여기서 우리는 이 비율이 다음 순간에 구매할 것인지 판매할 것인지 알 수 있는 신호를 만들려고 합니다. 즉, 우리의 예측 변수 Y:

Y = 비율은 구매 (1) 또는 판매 (-1) 입니다.

Y(t)= Sign(Ratio(t+1) Ratio(t))

우리는 실제 거래 목표 가격을 예측할 필요가 없거나 비율의 실제 값을 예측할 필요가 없다는 것을 참고하십시오 (우리가 할 수 있지만), 다음 단계에서는 비율 방향만 예측합니다.

단계 2: 신뢰성 있고 정확한 데이터를 수집

FMZ Quant는 당신의 친구입니다! 당신은 단지 거래되는 거래 객체와 사용해야 하는 데이터 소스를 지정해야 합니다. 그리고 그것은 필요한 데이터를 추출하고 배당과 거래 객체 분할을 위해 청소합니다. 그래서 여기 데이터는 매우 깨끗합니다.

지난 10년간의 거래일 (약 2500개의 데이터 포인트) 에 대해, 우리는 야후 파이낸스를 사용하여 다음과 같은 데이터를 얻었습니다. 오픈 가격, 종료 가격, 최고 가격, 최저 가격 및 거래량.

단계 3: 데이터를 분할합니다.

모델의 정확성을 테스트하는 매우 중요한 단계를 잊지 마십시오. 우리는 교육 / 검증 / 테스트 분할에 다음과 같은 데이터를 사용합니다.

  • 교육 7년 ~ 70%

  • 테스트 ~ 3년 30%

ratios = data['ADBE'] / data['MSFT']
print(len(ratios))
train = ratios[:1762]
test = ratios[1762:]

이상적으로는 검증 집합도 만들어야 하지만 지금은 그렇게 하지 않을 겁니다.

단계 4: 특징 엔지니어링

관련 함수는 무엇입니까? 우리는 비율 변화의 방향을 예측하고 싶습니다. 우리는 우리의 두 거래 목표가 통합되어 있음을 보았습니다. 따라서이 비율은 이동하고 평균 값으로 돌아갈 경향이 있습니다. 우리의 특성이 평균 비율의 몇 가지 척도가어야하며 현재 가치와 평균 가치 사이의 차이는 우리의 거래 신호를 생성 할 수 있습니다.

우리는 다음과 같은 함수를 사용합니다.

  • 60일 이동평균 비율: 롤링 평균을 측정합니다.

  • 5일 이동평균 비율: 평균의 현재 값을 측정합니다.

  • 60일 표준편차

  • Z 점수: (5d MA - 60d MA) / 60d SD.

ratios_mavg5 = train.rolling(window=5,
                               center=False).mean()
ratios_mavg60 = train.rolling(window=60,
                               center=False).mean()
std_60 = train.rolling(window=60,
                        center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()

img

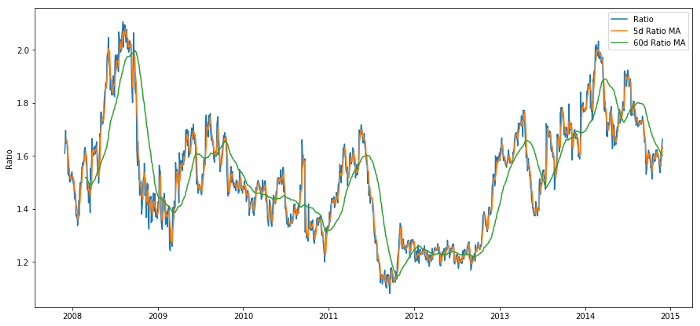
60d와 5d MA 사이의 가격 비율

plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()

img

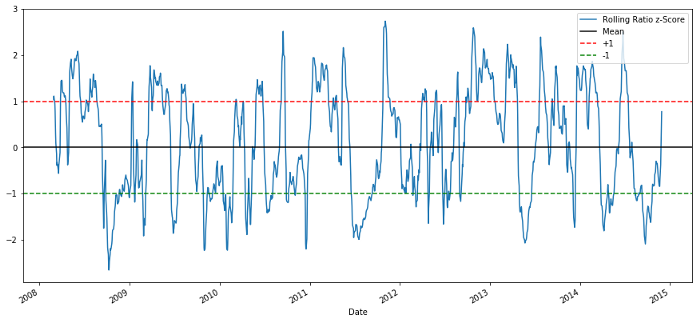
60-5 Z 점수 가격 비율

롤링 평균 값의 Z 점수는 비율의 평균 값 회귀 특성을 나타냅니다!

단계 5: 모델 선택

z 점수 차트를 보면 z 점수가 너무 높거나 너무 낮으면 다시 돌아오는 것을 볼 수 있습니다. 너무 높고 너무 낮다는 것을 정의하기 위해 +1/- 1을 임계값으로 사용해보죠. 그리고 다음 모델을 사용하여 거래 신호를 생성할 수 있습니다.

  • z가 -1.0보다 작을 때, 비율은 (1) 를 구매해야 합니다. z가 0으로 돌아갈 것으로 예상하기 때문에, 비율은 증가합니다.

  • z가 1.0보다 높을 때, 비율은 판매 (- 1) 입니다. z가 0으로 돌아갈 것으로 예상하기 때문에 비율은 감소합니다.

단계 6: 훈련, 검증 및 최적화

마지막으로, 실제 데이터에 우리의 모델의 실제 영향을 살펴보자. 실제 비율에 이 신호의 성능을 살펴보자.

# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color=’g’, linestyle=’None’, marker=’^’)
sell[60:].plot(color=’r’, linestyle=’None’, marker=’^’)
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend([‘Ratio’, ‘Buy Signal’, ‘Sell Signal’])
plt.show()

img

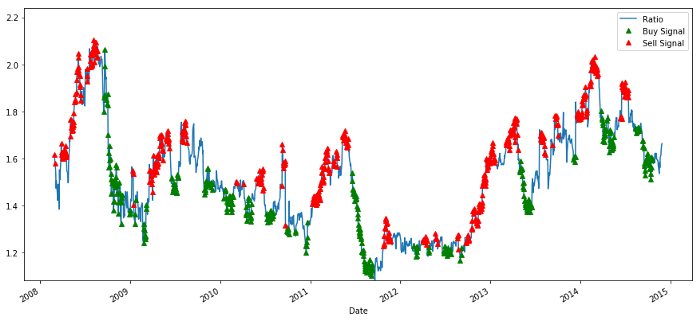
구매 및 판매 가격 비율 신호

신호는 합리적으로 보인다. 우리는 높은 또는 증가 (붉은 점) 을 판매하고 낮은 (녹색 점) 및 감소 할 때 다시 구입하는 것처럼 보입니다. 이것은 우리의 거래의 실제 주제에 대해 무엇을 의미합니까? 보자:

# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1 = data['ADBE'].iloc[:1762]
S2 = data['MSFT'].iloc[:1762]
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2 
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['ADBE','MSFT', 'Buy Signal', 'Sell Signal'])
plt.show()

img

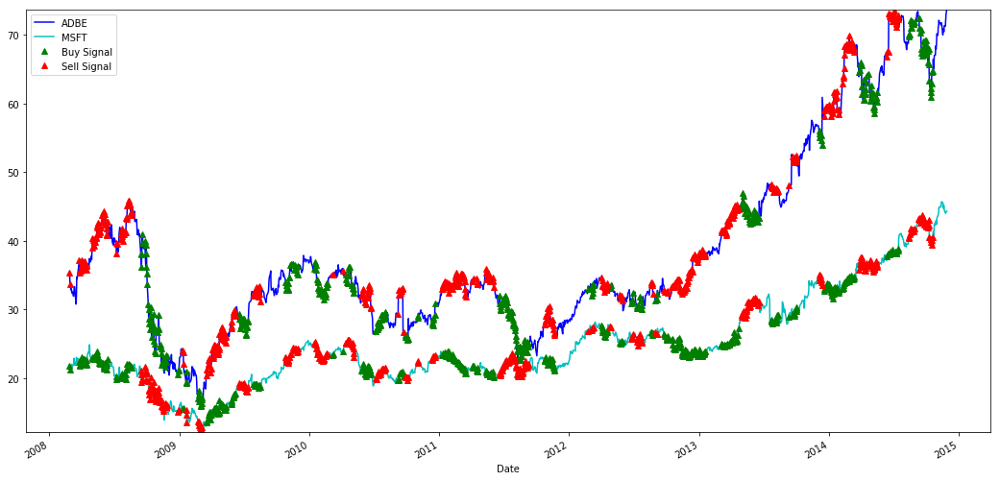
MSFT 및 ADBE 주식 구매 및 판매 신호

가끔은 단발, 가끔은 장발, 가끔은 둘 다로 수익을 올리는 것에 주의를 기울여 주십시오.

우리는 훈련 데이터의 신호에 만족합니다. 이 신호가 어떤 종류의 이익을 창출 할 수 있는지 보자. 비율이 낮을 때, 우리는 간단한 백 테스터를 만들 수 있습니다. 비율을 구입하고 (ADBE 주식 1 개 구입하고 MSFT 주식 x 판매 비율) 비율을 판매하고 (ADBE 주식 1 개 판매하고 MSFT 주식 x 구매 비율) 비율이 높을 때 이러한 비율의 PnL 거래를 계산합니다.

# Trade using a simple strategy
def trade(S1, S2, window1, window2):
    
    # If window length is 0, algorithm doesn't make sense, so exit
    if (window1 == 0) or (window2 == 0):
        return 0
    
    # Compute rolling mean and rolling standard deviation
    ratios = S1/S2
    ma1 = ratios.rolling(window=window1,
                               center=False).mean()
    ma2 = ratios.rolling(window=window2,
                               center=False).mean()
    std = ratios.rolling(window=window2,
                        center=False).std()
    zscore = (ma1 - ma2)/std
    
    # Simulate trading
    # Start with no money and no positions
    money = 0
    countS1 = 0
    countS2 = 0
    for i in range(len(ratios)):
        # Sell short if the z-score is > 1
        if zscore[i] > 1:
            money += S1[i] - S2[i] * ratios[i]
            countS1 -= 1
            countS2 += ratios[i]
            print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
        # Buy long if the z-score is < 1
        elif zscore[i] < -1:
            money -= S1[i] - S2[i] * ratios[i]
            countS1 += 1
            countS2 -= ratios[i]
            print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
        # Clear positions if the z-score between -.5 and .5
        elif abs(zscore[i]) < 0.75:
            money += S1[i] * countS1 + S2[i] * countS2
            countS1 = 0
            countS2 = 0
            print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
            
            
    return money
trade(data['ADBE'].iloc[:1763], data['MSFT'].iloc[:1763], 60, 5)

결과는 1783.375입니다.

그래서 이 전략은 수익성이 있는 것 같습니다. 이제, 우리는 이동 평균 시간 창을 변경하여, 구매/판매 및 폐쇄 포지션의 문턱을 변경하여, 그리고 검증 데이터의 성능 향상을 확인함으로써 더 이상 최적화 할 수 있습니다.

우리는 또한 더 복잡한 모델을 시도할 수 있습니다. 예를 들어, 로지스틱 회귀와 SVM, 1/-1을 예측하기 위해서요.

이제 이 모델을 발전시켜 봅시다.

단계 7: 테스트 데이터를 백테스트합니다

여기서도 FMZ 퀀트 플랫폼은 고성능 QPS/TPS 백테스팅 엔진을 채택하여 역사적 환경을 진정으로 재현하고 일반적인 양적 백테스팅 함정을 제거하고 전략의 결함을 적시에 발견하여 실제 봇 투자를 더 잘 도울 수 있습니다.

원리를 설명하기 위해, 이 기사는 여전히 근본적인 논리를 보여주는 것을 선택합니다. 실제 적용에서, 우리는 독자들이 FMZ 퀀트 플랫폼을 사용하는 것을 권장합니다. 시간을 절약하는 것 외에도 오류 관용율을 향상시키는 것이 중요합니다.

백테스팅은 간단합니다. 위의 함수를 사용하여 테스트 데이터의 PnL을 볼 수 있습니다.

trade(data['ADBE'].iloc[1762:], data['MSFT'].iloc[1762:], 60, 5)

결과는 5262,868입니다.

이 모델은 훌륭한 일을 했습니다. 우리의 첫 번째 간단한 쌍 거래 모델이 되었습니다.

너무 잘 맞지 않도록 합니다.

토론을 마무리하기 전에, 나는 특히 과잉 적합성에 대해 논의하고 싶습니다. 과잉 적합성은 거래 전략에서 가장 위험한 함정입니다. 과잉 적합 알고리즘은 백테스트에서 매우 잘 수행 할 수 있지만 새로운 보이지 않는 데이터에서 실패 할 수 있습니다. 이는 데이터의 어떤 추세를 실제로 드러내지 않으며 실제 예측 능력이 없다는 것을 의미합니다. 간단한 예를 들어 보겠습니다.

우리의 모델에서, 우리는 롤링 매개 변수를 사용하여 시간 창 길이를 추정하고 최적화합니다. 우리는 모든 가능성에 대해 간단하게 반복하고 합리적인 시간 창을 결정하고 모델의 최상의 성능에 따라 시간 길이를 선택 할 수 있습니다. 훈련 데이터의 pnl에 따라 시간 창 길이를 점수하기 위해 간단한 루프를 작성하고 최상의 루프를 찾을 수 있습니다.

# Find the window length 0-254 
# that gives the highest returns using this strategy
length_scores = [trade(data['ADBE'].iloc[:1762], 
                data['MSFT'].iloc[:1762], l, 5) 
                for l in range(255)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)

('Best window length:', 40)

이제 우리는 테스트 데이터에 대한 모델의 성능을 조사하고, 우리는 이 시간 창 길이가 최적과는 거리가 멀다는 것을 발견합니다. 이것은 우리의 원래 선택이 표본 데이터에 명확하게 부합했기 때문입니다.

# Find the returns for test data
# using what we think is the best window length
length_scores2 = [trade(data['ADBE'].iloc[1762:], 
                  data['MSFT'].iloc[1762:],l,5) 
                  for l in range(255)]
print (best_length, 'day window:', length_scores2[best_length])
# Find the best window length based on this dataset, 
# and the returns using this window length
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])

(40, 'day window:', 1252233.1395)
(15, 'day window:', 1449116.4522)

우리에게 적합한 표본 데이터가 항상 좋은 결과를 가져올 수 없다는 것은 분명합니다. 테스트를 위해 두 데이터 세트에서 계산된 길이 점수를 그래프로 그려 봅시다.

plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()

img

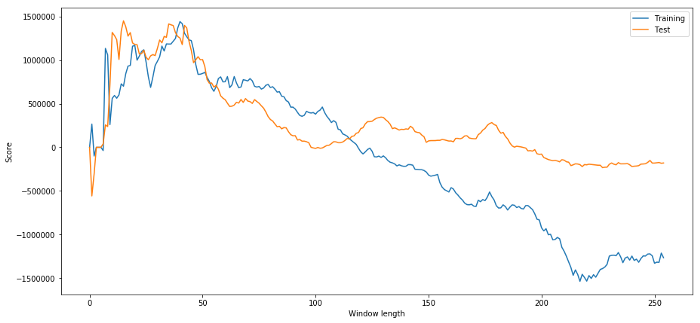
우리는 20~50 사이가 시간 창에 좋은 선택이라는 것을 알 수 있습니다.

과도한 적합성을 피하기 위해 경제 추론 또는 알고리즘의 본질을 사용하여 시간 창의 길이를 선택할 수 있습니다. 또한 길이를 지정 할 필요가 없는 칼만 필터를 사용할 수 있습니다. 이 접근법은 나중에 다른 기사에서 설명 될 것입니다.

다음 단계

이 기사에서는 거래 전략을 개발하는 과정을 보여주기 위해 몇 가지 간단한 소개 방법을 제안합니다. 실제로는 더 복잡한 통계를 사용해야합니다. 다음 옵션을 고려할 수 있습니다:

  • 허스트 지수;

  • 오른슈타인-울렌베크 공정에서 추론된 평균 회귀의 반감기

  • 칼만 필터

관련
더 많은

2019 FMZ - 모든 권리 보호