긴 짧은 포지션에 대한 균형 잡힌 주식 전략과 체계적인 조화를 달성

긴 짧은 포지션에 대한 균형 잡힌 주식 전략과 체계적인 조화를 달성

이전 기사에서 (https://www.fmz.com/bbs-topic/9862), 우리는 쌍 거래 전략을 소개하고 데이터와 수학적 분석을 사용하여 거래 전략을 만들고 자동화하는 방법을 보여주었습니다.

긴 짧은 포지션 균형 주식 전략은 거래 대상의 바구니에 적용되는 쌍 거래 전략의 자연스러운 확장입니다. 디지털 통화 시장과 상품 선물 시장과 같은 많은 종류와 상호 관계를 가진 거래 시장에 특히 적합합니다.

기본 원칙

롱 쇼트 포지션 균형 주식 전략은 거래 목표의 바구니를 동시에 길게하고 짧게하는 것입니다. 페어 거래와 마찬가지로 어느 투자 목표가 저렴하고 어느 투자 목표가 비싸지를 결정합니다. 차이점은 롱 쇼트 포지션 균형 주식 전략이 어느 투자 목표가 상대적으로 저렴하거나 비싸지 않은지 결정하기 위해 모든 투자 목표를 주식 선택 풀에 배치한다는 것입니다. 그 다음 순위에 따라 상위 n 투자 목표를 길게하고 아래 n 투자 목표를 동일한 금액으로 짧게합니다. (장 포지션의 총 가치 = 짧은 포지션의 총 가치).

쌍 거래는 시장 중립 전략이라고 말한 것을 기억하십니까? 긴 짧은 포지션 균형 주식 전략에도 마찬가지입니다. 긴 포지션과 짧은 포지션의 동일한 양이 전략이 시장 중립 (시장 변동에 영향을 받지 않습니다) 로 유지되도록 보장하기 때문입니다. 전략은 또한 통계적으로 견고합니다; 투자 목표를 순위화하고 긴 포지션을 보유함으로써 순위 모델에서 여러 번 포지션을 열 수 있습니다. 한 번 위험 오픈 포지션이 아닙니다. 당신은 순전히 순위 스키마의 품질에 베팅합니다.

순위계획은 어떤가요?

순위 체계는 예상된 성과에 따라 각 투자 대상에 우선 순위를 부여할 수 있는 모델이다. 요인은 가치 요인, 기술적 지표, 가격 모델 또는 위의 모든 요인의 조합이 될 수 있다. 예를 들어, 동력 지표를 사용하여 일련의 트렌드 추적 투자 목표를 순위 지정할 수 있다. 가장 높은 동력을 가진 투자 목표가 계속해서 좋은 성과를 거두며 가장 높은 순위를 얻을 것으로 예상된다. 가장 낮은 동력을 가진 투자 대상은 최악의 성과와 가장 낮은 수익을 가지고 있다.

이 전략의 성공은 거의 전적으로 사용 된 순위 체계에 달려 있습니다. 즉, 순위 체계는 높은 성능 투자 목표와 낮은 성능 투자 목표를 분리 할 수 있습니다. 따라서 장기 및 짧은 포지션 투자 목표의 전략의 수익을 더 잘 실현 할 수 있습니다. 따라서 순위 시스템을 개발하는 것이 매우 중요합니다.

어떻게 순위계획을 만들까요?

일단 순위제를 결정하면, 우리는 그로부터 이익을 얻을 수 있기를 희망합니다. 우리는 상위 투자 목표를 길게하고 최하위 투자 목표를 짧게하기 위해 동일한 자본을 투자함으로써 이것을합니다. 이것은 전략이 순위 품질에 비례하여 수익을 창출 할 것이며, 그것은 "시장 중립"일 것입니다.

모든 투자 목표 m를 순위 지정하고 있으며 투자에 필요한 달러가 n 개이며 총 2p (m>2p) 포지션을 보유하기를 원한다고 가정합니다. 투자 대상 순위 1이 최악의 성과를 낼 것으로 예상되는 경우 투자 대상 순위 m가 가장 좋은 성과를 낼 것으로 예상됩니다.

• 투자 대상을 이렇게 순위 지정합니다: 1,...,p 위치, 2/2p USD의 투자 목표를 단축합니다.

• 투자 대상을 이렇게 순위 지정합니다: m-p,...,m 위치, n/2p USD의 투자 목표를 길게 이동합니다.

참고: 가격 변동으로 인해 발생하는 투자 대상 물가의 값이 항상 n/2p를 균등하게 나눌 수 없으며 일부 투자 대상 물품은 정수로 구입해야하기 때문에 가능한 한이 숫자에 가깝게 접근해야하는 몇 가지 부정확한 알고리즘이있을 것입니다. n=100000과 p=500을 실행하는 전략에서 우리는 다음과 같이 볼 수 있습니다.

n/2p = 100000/1000 = 100

이것은 100 이상의 가격 (상품 선물 시장과 같이) 을 가진 점수에 큰 문제를 일으킬 것입니다. 왜냐하면 분량 가격으로 위치를 열 수 없기 때문입니다 (이 문제는 디지털 통화 시장에서 존재하지 않습니다). 분량 가격 거래를 줄이거나 자본을 증가시킴으로써이 상황을 완화합니다.

가상의 예를 들어보죠.

• FMZ 퀀트 플랫폼에 우리의 연구 환경을 구축

우선, 원활한 작업을 위해, 우리는 우리의 연구 환경을 구축해야합니다. 이 기사에서는 FMZ 퀀트 플랫폼을 사용합니다 (FMZ.COM) 를 구축하기 위해 연구 환경을 구축했습니다. 주로 편리하고 빠른 API 인터페이스와 이 플랫폼의 잘 포장된 Docker 시스템을 나중에 사용할 수 있습니다.

FMZ 퀀트 플랫폼의 공식 명칭에서 이 도커 시스템은 도커 시스템이라고 불린다.

도커와 로봇을 어떻게 배포해야 하는지에 대한 제 이전 기사를 참조하시기 바랍니다:https://www.fmz.com/bbs-topic/9864.

독자들이 자신의 클라우드 컴퓨팅 서버를 구입하여 도커를 배포하고 싶다면 이 기사를 참조할 수 있습니다.https://www.fmz.com/digest-topic/5711.

클라우드 컴퓨팅 서버와 도커 시스템을 성공적으로 배포한 후, 다음으로 우리는 파이썬의 현재 가장 큰 유물을 설치합니다: 아나콘다

이 문서에서 요구되는 모든 관련 프로그램 환경 ( 의존성 라이브러리, 버전 관리 등) 을 구현하기 위해 가장 간단한 방법은 아나콘다를 사용하는 것입니다. 그것은 패키지 된 파이썬 데이터 과학 생태계 및 의존성 라이브러리 관리자입니다.

아나콘다의 설치 방법에 대해서는 아나콘다의 공식 가이드를 참조하십시오.https://www.anaconda.com/distribution/.

이 문서에서는 또한 파이썬 과학 컴퓨팅에서 두 가지 인기 있고 중요한 라이브러리인 numpy와 panda를 사용할 것입니다.

위의 기본 작업은 아나콘다 환경 및 피 및 판다 라이브러리를 설정하는 방법에 대해 소개하는 이전 기사를 참조 할 수 있습니다. 자세한 내용은 참조하십시오:https://www.fmz.com/digest-topic/9863.

우리는 임의의 투자 목표와 임의의 요인을 생성하여 순위를 매깁니다. 우리의 미래 수익이 실제로 이러한 요인 값에 의존한다고 가정해 봅시다.

import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
## PROBLEM SETUP ##
# Generate stocks and a random factor value for them
stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)
# Generate future returns for these are dependent on our factor values
future_returns = current_factor_values + np.random.normal(0, 1, 10000)
# Put both the factor values and returns into one dataframe
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

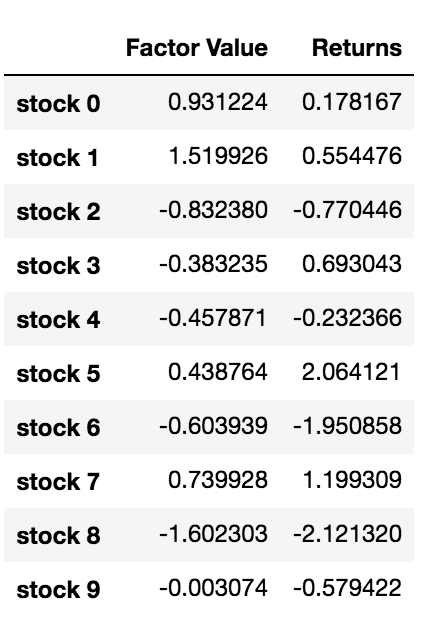
이제 우리는 요인 값과 수익을 가지고 있습니다. 만약 우리가 요인 값에 따라 투자 목표를 순위화하고,

# Rank stocks
ranked_data = data.sort_values('Factor Value')
# Compute the returns of each basket with a basket size 500, so total (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)
for i in range(number_of_baskets):
    start = i * 500
    end = i * 500 + 500 
    basket_returns[i] = ranked_data[start:end]['Returns'].mean()
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

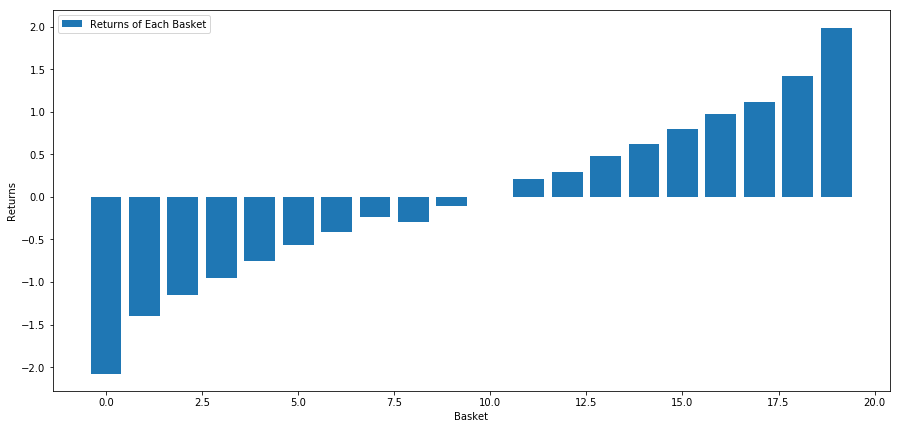
우리의 전략은 투자 대상 풀의 첫 번째 순위 바구니를 길게하고 10 순위 바구니를 짧게하는 것입니다. 이 전략의 수익은 다음과 같습니다.

basket_returns[number_of_baskets-1] - basket_returns[0]

결과는 4.172입니다.

우리의 순위 모델에 돈을 투자해 높은 성과를 내는 투자 목표와 낮은 성과를 내는 투자 목표를 분리할 수 있도록 말이죠.

이 문서의 나머지 부분에서는 순위 제도를 평가하는 방법에 대해 논의 할 것입니다. 순위 기반의 중재의 장점은 시장 장애에 영향을받지 않고 시장 장애가 사용될 수 있다는 것입니다.

실제 세계의 예를 생각해 봅시다.

우리는 S&P 500 지표에 있는 32개의 다른 업종의 주식들에 대한 데이터를 로드해서 순위를 매기려고 했습니다.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
                'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
                'HD','LOW','KO','LLY','MCD','MET','NEM',
                'PEP','PG','M','SWN','T','TGT',
                'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
price = 'adjClose'

한 달 동안 표준화 된 추진력 지표를 순위 기준으로 사용해보자.

## Define normalized momentum
def momentum(dataDf, period):
    return dataDf.sub(dataDf.shift(period), fill_value=0) / dataDf.iloc[-1]
## Load relevant prices in a dataframe
data = ds.getBookDataByFeature()['Adj Close']
#Let's load momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

이제 우리는 주식의 행동을 분석하고 우리가 선택한 순위 요인에서 시장에서 주식이 어떻게 작동하는지 볼 것입니다.

데이터를 분석합니다.

주식 행동

선택된 주식 바구니가 순위 모델에서 어떻게 작동하는지 살펴보자. 이를 위해 모든 주식의 주간 포워드 수익을 계산해 보자. 그러면 각 주식의 1주간의 포워드 수익과 전 30일의 동력 사이의 상관관계를 볼 수 있다. 긍정적인 상관관계를 보이는 주식은 트렌드 추종자이고, 부정적인 상관관계를 보이는 주식은 평균 반전이다.

# Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = True)
# Calculate correlations between momentum and returns
correlations = pd.DataFrame(index = returns.columns, columns = ['Scores', 'pvalues'])
mscores = mscores[mscores.index.isin(returns.index)]
for i in correlations.index:
    score, pvalue = stats.spearmanr(mscores[i], returns[i])
    correlations[‘pvalues’].loc[i] = pvalue
    correlations[‘Scores’].loc[i] = score
correlations.dropna(inplace = True)
correlations.sort_values('Scores', inplace=True)
l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations['Scores'])
plt.xlabel('Stocks')
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.legend(['Correlation over All Data'])
plt.ylabel('Correlation between %s day Momentum Scores and %s-day forward returns by Stock'%(day,forward_return_day));
plt.show()

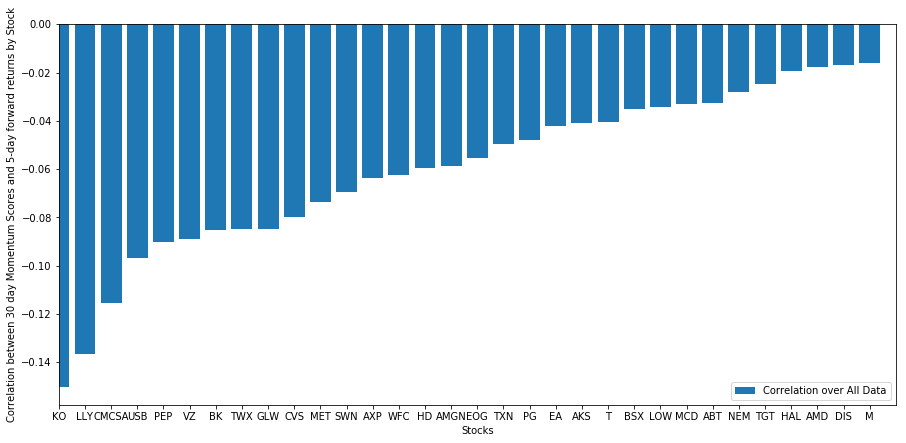
모든 주식들은 어느 정도 평균 회귀를 가지고 있습니다! (우리가 선택한 우주는 분명히 이렇게 작동합니다.) 이것이 우리에게 주식들이 모멘텀 분석에서 상위권을 차지한다면 다음 주에 저조한 성과를 기대해야한다는 것을 알려줍니다.

모멘텀 분석 점수 순위와 수익 사이의 상관관계

다음으로, 우리는 우리의 순위 점수와 시장의 전체 전향 수익률 사이의 상관관계를 볼 필요가 있습니다. 즉 예측된 수익률과 우리의 순위 요인 사이의 관계입니다. 더 높은 상관관계 수준은 더 낮은 상대적 수익률을 예측할 수 있습니까? 또는 그 반대의 경우?

이 목적을 위해, 우리는 모든 주식의 30일 동력과 1주 전속 수익 사이의 일일 상관관계를 계산합니다.

correl_scores = pd.DataFrame(index = returns.index.intersection(mscores.index), columns = ['Scores', 'pvalues'])
for i in correl_scores.index:
    score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
    correl_scores['pvalues'].loc[i] = pvalue
    correl_scores['Scores'].loc[i] = score
correl_scores.dropna(inplace = True)
l = correl_scores.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correl_scores['Scores'])
plt.hlines(np.mean(correl_scores['Scores']), 1,l+1, colors='r', linestyles='dashed')
plt.xlabel('Day')
plt.xlim((1, l+1))
plt.legend(['Mean Correlation over All Data', 'Daily Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

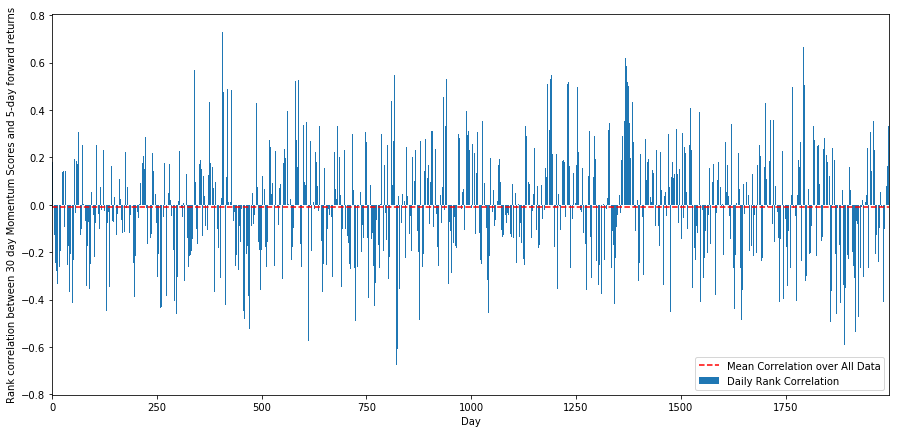
일일 상관관계는 매우 복잡하지만 매우 가벼운 상관관계를 보여줍니다 (모든 주가가 평균으로 돌아갈 것이라고 말했기 때문에 예상됩니다). 우리는 또한 1 개월의 전속 수익의 평균 월간 상관관계를 살펴야합니다.

monthly_mean_correl =correl_scores['Scores'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colors='r', linestyles='dashed')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

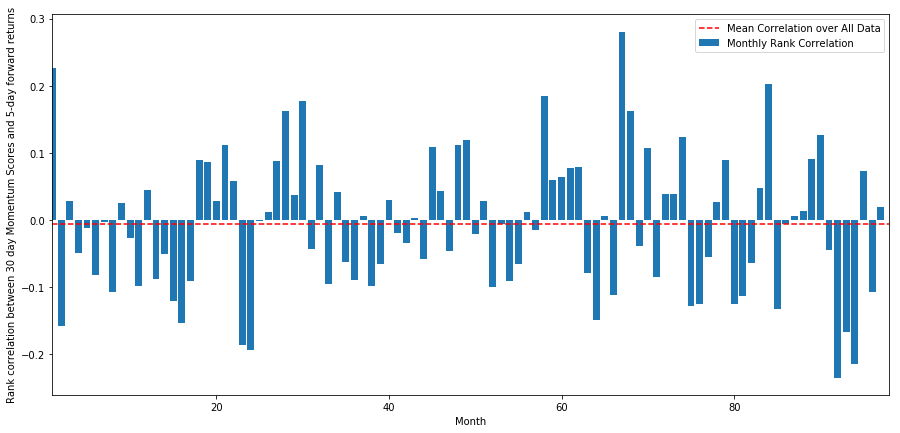
평균 상관관계가 다시 약간 부정적이라는 것을 볼 수 있습니다. 하지만 그것은 또한 매달 크게 변합니다.

주식 카스켓의 평균 수익률

우리는 순위에서 가져온 주식 바구니의 수익률을 계산했습니다. 모든 주식을 순위화하고 n 그룹으로 나누면 각 그룹의 평균 수익률은 무엇입니까?

첫 번째 단계는 매월 주어진 각 바구니의 평균 수익률과 순위 요인을 제공하는 함수를 만드는 것입니다.

def compute_basket_returns(factor, forward_returns, number_of_baskets, index):
data = pd.concat([factor.loc[index],forward_returns.loc[index]], axis=1)
    # Rank the equities on the factor values
    data.columns = ['Factor Value', 'Forward Returns']
    data.sort_values('Factor Value', inplace=True)
    # How many equities per basket
    equities_per_basket = np.floor(len(data.index) / number_of_baskets)
basket_returns = np.zeros(number_of_baskets)
# Compute the returns of each basket
    for i in range(number_of_baskets):
        start = i * equities_per_basket
        if i == number_of_baskets - 1:
            # Handle having a few extra in the last basket when our number of equities doesn't divide well
            end = len(data.index) - 1
        else:
            end = i * equities_per_basket + equities_per_basket
        # Actually compute the mean returns for each basket
        #s = data.index.iloc[start]
        #e = data.index.iloc[end]
        basket_returns[i] = data.iloc[int(start):int(end)]['Forward Returns'].mean()
        
    return basket_returns

이 점수를 기준으로 주식을 순위를 매기는 것은 각 바구니의 평균 수익률을 계산하는 것입니다.

number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(float).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = True)
for m in forward_returns.index.intersection(resampled_scores.index):
    basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
    mean_basket_returns += basket_returns
mean_basket_returns /= l    
print(mean_basket_returns)
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

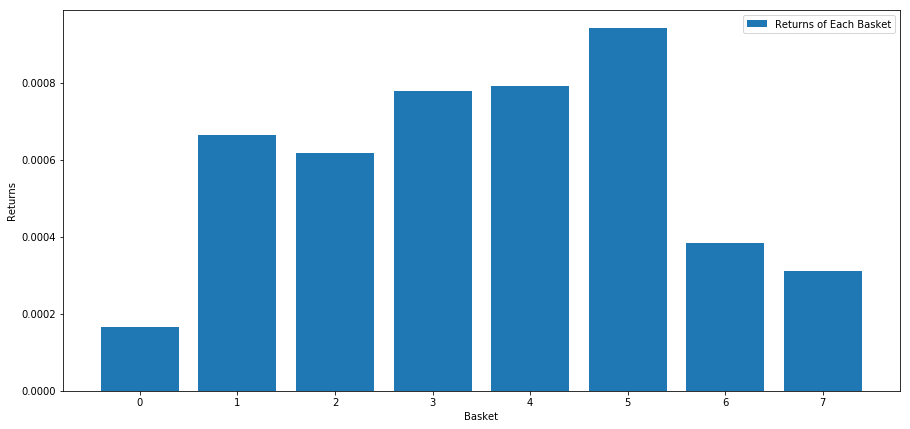
높은 성과를 내는 사람과 낮은 성과를 내는 사람을 구분할 수 있는 것 같습니다.

마진 (기반) 의 일관성

물론, 이것들은 단지 평균적인 관계입니다. 관계가 얼마나 일관성 있고 우리가 거래하기를 원하는지 이해하기 위해서는 시간이 지남에 따라 접근 방식과 태도를 변경해야합니다. 다음으로, 우리는 이전 2 년 동안의 월간 이자 마진 (기반) 을 살펴볼 것입니다. 우리는 더 많은 변화를 볼 수 있으며 이 추진 스코어가 거래 될 수 있는지 여부를 결정하기 위해 추가 분석을 수행 할 수 있습니다.

total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
    temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[month]]
    temp_scores = resampled_scores.loc[monthly_index[month-1]:monthly_index[month]]
    for m in temp_returns.index.intersection(temp_scores.index):
        basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
        mean_basket_returns += basket_returns
    
    strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
    
    mean_basket_returns /= temp_returns.index.intersection(temp_scores.index).size
    
    r = int(np.floor((month-1) / 6))
    c = (month-1) % 6
    axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
    axarr[r, c].xaxis.set_visible(False)
    axarr[r, c].set_title('Month ' + str(month))
plt.show()

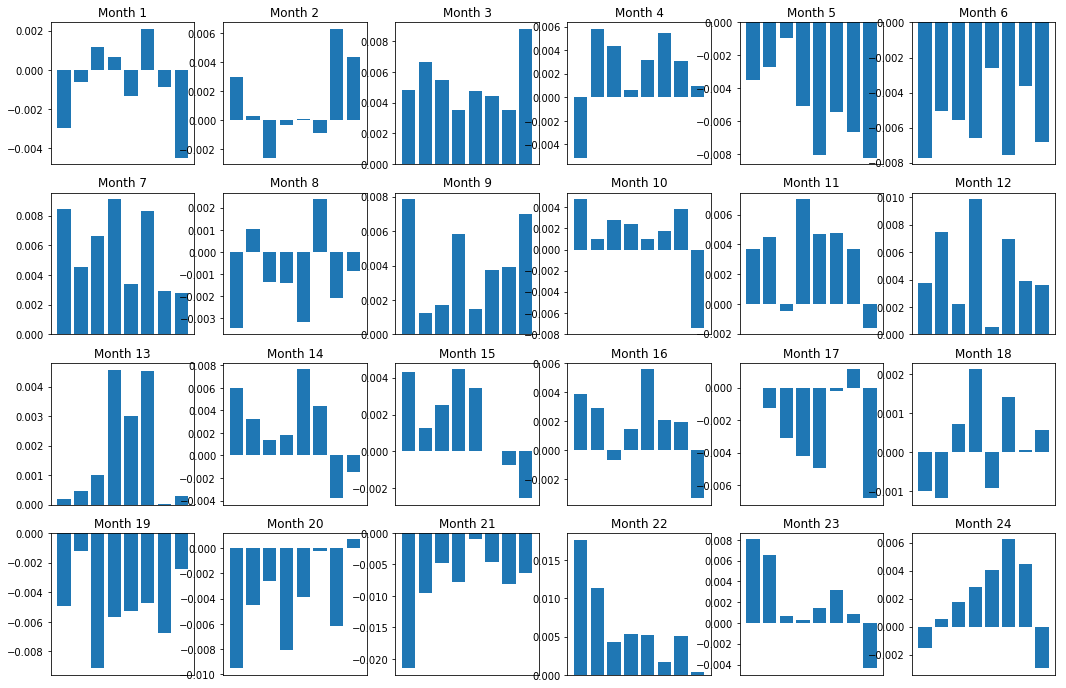
plt.figure(figsize=(15,7))
plt.plot(strategy_returns)
plt.ylabel('Returns')
plt.xlabel('Month')
plt.plot(strategy_returns.cumsum())
plt.legend(['Monthly Strategy Returns', 'Cumulative Strategy Returns'])
plt.show()

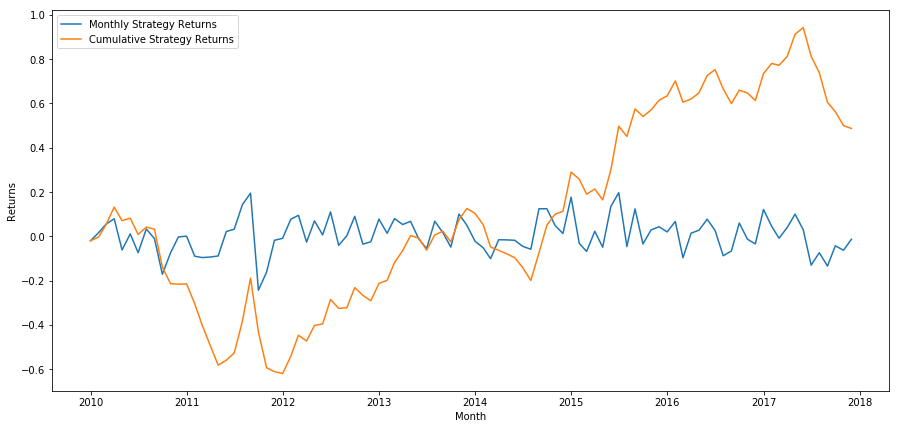
마지막으로, 우리가 마지막 바구니에 장과 첫 번째 바구니에 단장을 매월 한다면, 수익률을 살펴봅시다 (보증권당 동일한 자본 분배를 가정하면).

total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

연간 수익률: 5.03%

우리는 매우 약한 순위 체계가 있다는 것을 알 수 있습니다. 높은 성과를 내는 주식과 낮은 성과를 내는 주식을 가볍게 구별할 수 있습니다. 게다가 이 순위 체계는 일관성이 없으며 매달 크게 변합니다.

올바른 순위계획을 찾습니다.

롱 쇼트 밸런스 엑시티 전략을 실현하기 위해, 실제로, 당신은 순위 스키마를 결정하는 것 만이 필요합니다. 그 다음 모든 것이 기계적입니다. 일단 당신이 롱 쇼트 밸런스 엑시티 전략을 가지고 나면, 당신은 많은 변화없이 다른 순위 요인을 교환 할 수 있습니다. 그것은 모든 코드를 매번 조정하는 것에 대해 걱정하지 않고 빠르게 아이디어를 반복하는 매우 편리한 방법입니다.

순위 체계는 또한 거의 모든 모델에서 나올 수 있습니다. 그것은 반드시 가치 기반 인자 모델이 아닙니다. 그것은 한 달 전에 수익을 예측하고 이 수준에 따라 순위를 매기는 기계 학습 기술이 될 수 있습니다.

순위 체계의 선택 및 평가

순위 체계는 장기 단기 균형 주식 전략의 장점이자 가장 중요한 부분입니다. 좋은 순위 체계를 선택하는 것은 체계적인 프로젝트이며 쉬운 답은 없습니다.

좋은 출발점은 기존의 알려진 기술을 선택하고 더 높은 수익을 얻기 위해 약간 수정 할 수 있는지 확인하는 것입니다. 여기 우리는 몇 가지 출발점을 논의 할 것입니다.

• 클론 및 조정: 자주 논의되는 주제를 선택하고 이점을 얻기 위해 약간 수정 할 수 있는지 확인하십시오. 일반적으로 공개 가능한 요소는 시장에서 완전히 중재되었기 때문에 더 이상 거래 신호가 없습니다. 그러나 때로는 올바른 방향으로 이끌 것입니다.

• 가격 모델: 미래의 수익을 예측하는 모든 모델은 잠재적으로 거래 대상의 바구니를 순위 지정하는 데 사용할 수있는 요소가 될 수 있습니다. 복잡한 가격 모델을 가져다가 순위 계획으로 변환 할 수 있습니다.

• 가격 기반 요인 (기술 지표): 오늘날 논의 된 가격 기반 요인은 각 주식의 역사적 가격에 대한 정보를 얻고 요인 값을 생성하는 데 사용합니다. 예를 들어 이동 평균 지표, 추진력 지표 또는 변동성 지표가 될 수 있습니다.

• 회귀 및 추진력: 일부 요소는 가격이 한 방향으로 움직이면 계속 움직일 것이라고 믿으며 일부 요소는 정반대의 것으로 간주되는 것을 주목할 가치가 있습니다. 둘 다 다른 시간 지평과 자산에 대한 효과적인 모델이며 기본 행동이 추진력이나 회귀에 기반하는지 연구하는 것이 중요합니다.

• 기본 요인 (가치 기반): PE, 배당 등 기본 가치의 조합입니다. 기본 가치는 회사의 실제 세계 사실과 관련된 정보를 포함하고 있으므로 많은 측면에서 가격보다 강력 할 수 있습니다.

궁극적으로, 개발 예측자는 군비 경쟁이고, 당신은 한 발 앞서 유지하려고 노력합니다. 요인은 시장에서 중재되고 유용한 수명을 가지고 있습니다. 그래서 당신은 끊임없이 당신의 요인이 얼마나 많은 불황을 경험하고 어떤 새로운 요인이 그들을 대체하는 데 사용할 수 있는지 결정하기 위해 노력해야합니다.

기타 고려 사항

• 재균형 주파수

각 순위 시스템은 약간 다른 시간 프레임에서 수익을 예측합니다. 가격에 기반한 평균 회귀는 며칠 내에 예측 될 수 있으며, 가치에 기반한 인자 모델은 몇 달 내에 예측 될 수 있습니다. 모델이 예측해야하는 시간 범위를 결정하고 전략을 실행하기 전에 통계 검증을 수행하는 것이 중요합니다. 물론, 당신은 재균형 주파수를 최적화하려고 노력함으로써 과잉 적합성을 원하지 않습니다. 당신은 필연적으로 다른 주파수보다 더 나은 무작위 주파수를 찾을 것입니다. 순위 스키마 예측의 시간 범위를 결정 한 후에는 모델을 완전히 사용하기 위해 이 주파수에서 재균형을 시도하십시오.

• 자본 용량 및 거래 비용

각 전략은 최소 및 최대 자본량을 가지고 있으며 최소 한계는 일반적으로 거래 비용에 의해 결정됩니다.

너무 많은 주식을 거래하면 높은 거래 비용으로 이어질 것입니다. 1,000개의 주식을 구입하고 싶다면, 각 재균형에 수천 달러가 소요됩니다. 귀하의 자본 기반은 전략이 생성하는 수익의 작은 부분을 차지할 수 있도록 거래 비용이 충분히 높아야 합니다. 예를 들어, 귀하의 자본이 100,000 달러이고 전략이 매달 1% (1,000 달러) 를 벌면, 이러한 모든 수익은 거래 비용에 의해 소비됩니다. 1,000 개 이상의 주식을 벌기 위해 수백만 달러의 자본으로 전략을 실행해야합니다.

가장 낮은 자산 문턱은 주로 거래된 주식 수에 따라 다릅니다. 그러나 최대 용량도 매우 높습니다. 장기 단편 균형 주식 전략은 장점을 잃지 않고 수백 만 달러의 거래를 할 수 있습니다. 이것은 사실입니다. 이 전략은 비교적 평형화가 드물기 때문입니다. 총 자산이 거래된 주식 수로 나눌 때 각 주식의 달러 가치가 매우 낮을 것입니다. 거래량이 시장에 영향을 미칠지 걱정할 필요가 없습니다. 1,000 주식을 거래한다고 가정하십시오. 즉 100,000,000 달러입니다. 매달 전체 포트폴리오를 재균형하면 각 주식은 한 달에 100,000 달러만 거래 할 것입니다. 대부분의 증권에 중요한 시장이 될만큼 충분하지 않습니다.

관련

더 많은