Mata wang kripto adalah satu kelas aset baru, dan penyelidik baru sahaja mula memahami kekuatan asas di sebalik pergerakan harga mereka dengan lebih baik. Satu kertas penyelidikan baru menunjukkan bahawa harga Bitcoin dapat dimodelkan dengan Metcalfe’s Law.

Ringkasan:

Kami menggunakan contoh untuk menunjukkan bahawa harga jangka panjang Bitcoin adalah tidak rawak, dan dapat dimodelkan sebagai fungsi pertumbuhan jumlah pengguna n dari masa ke masa. Kami menggunakan data Facebook dan Bitcoin yang diperhatikan, kami menyimpulkan hubungan antara harga, jumlah pengguna, dan masa, dan menunjukkan bahawa nilai pasaran yang diperoleh mungkin mematuhi fungsi pertumbuhan sigmoid Gompertz. Fungsi ini digunakan secara sejarah untuk menggambarkan pertumbuhan organisma hidup seperti bakteria, tumor, dan virus, dan mungkin mempunyai aplikasi tertentu dalam bidang ekonomi rangkaian.

Pengutipan penting dalam kajian akademik:

Artikel ini memberikan penjelasan ringkas mengenai pembentukan harga dalam ekosistem cryptocurrency yang baru dan sering disalahpahami. Dengan Bitcoin sebagai contoh, kami memberikan bukti empirik yang meyakinkan bahawa pembentukan harga bukanlah hasil serentak dari pelaburan emosi, tetapi berdasarkan pada prinsip ekonomi nilai yang baru-baru ini mula diiktiraf: ekonomi rangkaian.

Pemeriksaan harga bitcoin memberikan beberapa pemerhatian yang menarik yang secara langsung membantah mitos bahawa nilai bitcoin adalah misteri. Pertama, seperti yang telah lama disokong oleh penyokong, nilai mata wang bergantung kepada penggunaan dan penerimaan mata wang tersebut.

Hukum Metcalfe adalah berdasarkan pada persembahan matematik yang menggambarkan hubungan antara n pengguna. Oleh itu, nilai rangkaian V adalah fungsi bilangan pengguna n. Asas matematik hukum Metcalfe adalah berdasarkan pada sambungan berpasangan (contohnya, telefon). Jika terdapat empat orang dalam rangkaian yang menggunakan telefon, mungkin terdapat 3 + 2 + 1 = 6 sambungan secara keseluruhan.

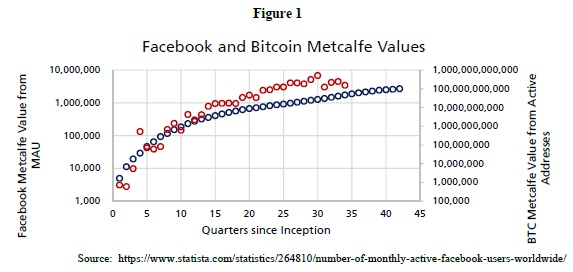
Facebook sangat sesuai untuk perbandingan dengan Bitcoin. Setiap siri data mempunyai panjang yang hampir sama (kira-kira 10 tahun). Kedua-duanya agak inovatif, walaupun tidak sepenuhnya asli (Digicash lebih awal daripada Bitcoin, MySpace lebih awal daripada Facebook).

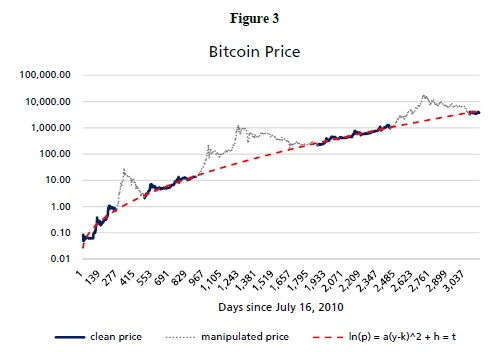
Kembali ke Rajah 3, terdapat tiga pengecualian yang patut diperhatikan, harga Bitcoin yang menyimpang dari trend parasol. Ini adalah tempoh di mana ada rekod manipulasi harga dan akhirnya mencapai keseimbangan. Puncak-puncak ini menunjukkan ketidakseimbangan harga yang tidak dapat dijelaskan oleh faktor yang berkaitan dengan pengguna. Faktor yang berkaitan dengan pengguna didorong oleh pertumbuhan pengguna atau penggunaan rangkaian. Faktor-faktor ini termasuk transaksi, akaun aktif, dompet, nod dan kadar hash.

Jika n tumbuh pada kadar yang tetap, maka log (n) adalah linear. Oleh kerana kita melihat log (n) tidak linear dalam Facebook dan Bitcoin (Rajah 7), maka n tumbuh pada kadar yang tidak tetap, menunjukkan bahawa adopsi berada dalam tahap yang berbeza. Model kadar pertumbuhan yang terkumpul ini menghasilkan fungsi bentuk S (fungsi Gompertz) yang telah digunakan selama beberapa dekad untuk mensimulasikan jangkitan virus, pertumbuhan bakteria, pertumbuhan tumor dan populariti telefon bimbit.[2018], beliau menggunakannya untuk mensimulasikan faktor kekerabatan Metcalfe. Menggunakan data harian n akaun aktif ejen, kami mencontohi persamaan ini dengan alamat aktif dalam Rajah 7.

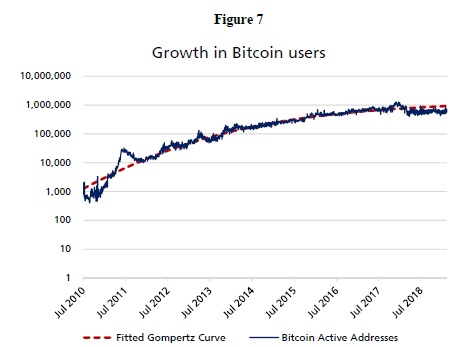
Terjemahan Bahasa Inggeris: