Mari kita bincangkan tentang cara mengoptimumkan parameter beberapa model dagangan terprogram

• #### Dataran Tinggi Parameter dan Pulau Parameter

　 Satu prinsip penting dalam pengoptimuman parameter adalah untuk mencapai dataran tinggi parameter dan bukan pulau parameter. Yang disebut dataran tinggi parameter, yang bermaksud terdapat satu parameter yang lebih luas, model dalam lingkungan parameter ini dapat mencapai kesan yang lebih baik, biasanya dengan pusat dataran tinggi membentuk bentuk yang hampir normal. Yang disebut dataran rendah parameter, yang bermaksud bahawa model hanya mempunyai prestasi yang baik apabila nilai parameter berada di dalam sesuatu yang sangat kecil, dan apabila parameter menyimpang dari nilai tersebut, prestasi model akan berubah secara ketara.

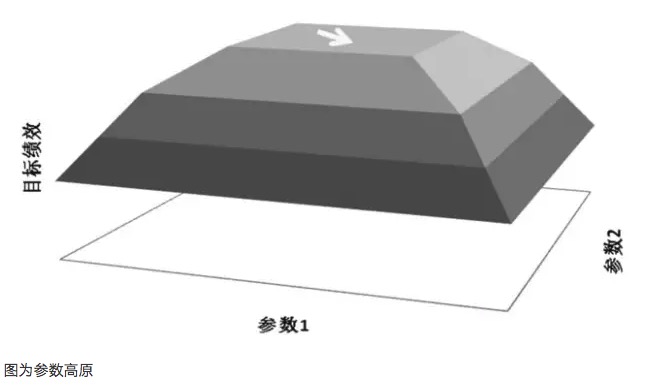
• #### Garis berparameter

Sebagai contoh, jika model dagangan mempunyai dua parameter, iaitu parameter 1 dan parameter 2, apabila kedua-dua parameter diuji secara berulang, ia akan menghasilkan peta prestasi tiga dimensi. Sebaran parameter yang baik harus menjadi parameter yang tinggi, walaupun apabila parameter parameter telah dipindahkan, prestasi model yang menguntungkan masih dapat dijamin.

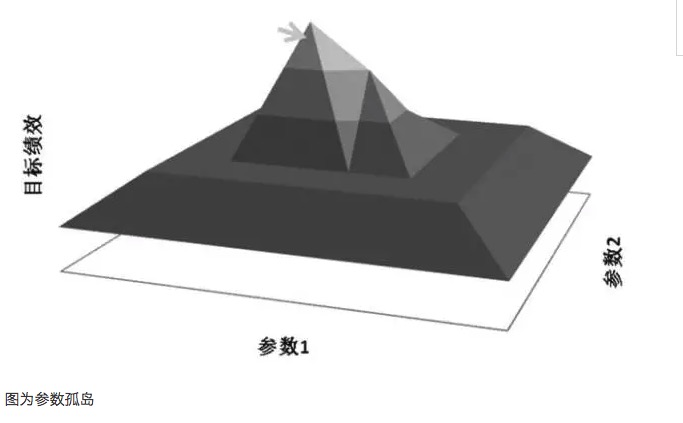
Secara amnya, jika sistem parameter berdekatan kurang baik daripada parameter optimum, maka parameter optimum ini mungkin merupakan hasil penjumlahan yang berlebihan, yang secara matematik boleh dianggap sebagai penyelesaian yang unik, dan bukan penyelesaian nilai yang sangat besar yang dicari. Dari segi matematik, keanehan adalah tidak stabil, dan dalam keadaan yang tidak pasti di masa depan, parameter optimum mungkin berubah menjadi parameter paling buruk apabila ciri-ciri pasaran berubah.

Overfitting berkaitan dengan sampel yang dipilih, jika sampel yang dipilih tidak dapat mewakili ciri-ciri keseluruhan pasaran, hanya untuk membuat keputusan ujian mencapai nilai yang diharapkan positif, amalan ini pasti menipu diri sendiri, nilai parameter yang diperolehi adalah nilai parameter yang tidak berkesan yang terlalu sesuai. Sebagai contoh, dengan menganalisis parameter yang terlalu sesuai, model perdagangan menunjukkan peningkatan kadar pulangan pada nilai 35 dan 63 masing-masing, jika indikator yang sesuai dalam model dipilih sebagai parameter 35 dan 63, hasil model kelihatan sempurna, tetapi sebenarnya adalah kesan pulau parameter yang khas.

Perselisihan utama antara overfit dan pengoptimuman parameter adalah bahawa parameter optimum yang diperoleh dengan pengoptimuman parameter model hanya berdasarkan sampel data sejarah yang telah berlaku, dan perlakuan masa depan adalah perubahan dinamik, yang mempunyai persamaan dan variasi berbanding dengan perlakuan sejarah. Pereka model dapat mencari parameter model yang berprestasi terbaik dalam sejarah, tetapi parameter ini tidak semestinya berprestasi terbaik dalam aplikasi sebenar model masa depan, apalagi parameter model yang berprestasi terbaik dalam sejarah, mungkin merupakan parameter yang berprestasi buruk dalam pertempuran model masa depan, bahkan membawa kerugian besar.

Di samping itu, dataran tinggi parameter dan pulau parameter sering mempunyai hubungan yang lebih besar dengan jumlah transaksi. Jika model mempunyai jumlah transaksi yang lebih sedikit, sering dapat mencari titik parameter yang sesuai, menjadikan model mendapat keuntungan dalam beberapa transaksi, keuntungan model yang dioptimumkan dengan parameter ini mencerminkan keacakan yang lebih kuat.

• #### Kaedah untuk mengoptimumkan parameter

Setelah mengetahui kawasan tinggi parameter dan pulau parameter, kaedah pengoptimuman parameter menjadi sangat penting, terutamanya apabila terdapat lebih banyak parameter dalam model (disebut susunan parameter), sering kali pengambilan nilai parameter akan mempengaruhi peredaran kawasan tinggi parameter yang lain. Jadi bagaimana pengoptimuman susunan parameter?

Salah satu kaedah ialah pendekatan penumpuan beransur-ansur. Iaitu, satu parameter dioptimumkan secara berasingan, dan ia akan tetap pada nilai terbaiknya, kemudian satu lagi parameter dioptimumkan, dan ia akan tetap pada nilai terbaiknya. Ia akan berputar sehingga hasilnya tidak berubah. Sebagai contoh, dalam model perdagangan runcit linear, kedua-dua parameter bebas adalah jangka pendek N1 dan jangka panjang N2. Pertama, N2 ditetapkan sebagai 1, N1 disaring untuk ujian, mencari nilai terbaik dalam julat 1 hingga 100, dan akhirnya parameter terbaik adalah 8 dan tetap; kedua, N2 dioptimumkan antara 1 hingga 200, dan nilai terbaik adalah 26 dan tetap; sekali lagi, N1 dioptimumkan untuk pusingan kedua, dan nilai terbaik baru adalah 10 dan tetap; dan akhirnya, N2 dioptimumkan dan nilai terbaiknya ditetapkan.

Kaedah lain ialah menggunakan platform reka bentuk perisian berprogram dengan fungsi pengiraan yang lebih kuat, terus mengira pengedaran antara fungsi sasaran dan argumen argumen, kemudian mencari pengedaran perbezaan multidimensi, menentukan had perbezaan, dengan nilai mutlak perbezaan kurang daripada had had yang sesuai dalam ruang dimensi dimensi terbesar, radius bola dalaman dalaman multidimensi tertinggi, dipilih sebagai nilai parameter yang paling stabil.

Selain kaedah pengoptimuman parameter, pemilihan sampel data juga merupakan faktor penting. Model yang mengikuti trend sebagai idea perdagangan berfungsi dengan baik dalam keadaan trend, dan strategi yang menjual atau membeli dengan harga tinggi sebagai idea perdagangan berfungsi dengan baik dalam keadaan bergolak. Oleh itu, dalam pengoptimuman parameter, anda perlu membuang tindakan yang sesuai dengan pemikiran perdagangan untuk mempertimbangkan keuntungan, dan menambah data tindakan yang tidak sesuai dengan pemikiran strategi untuk mempertimbangkan kerugian.

Sebagai contoh, indeks saham berjangka, pada tahun 2010 pada awal penyenaraian dan pada akhir tahun 2014 ketika berlaku keadaan bull market yang melampau, indeks saham berjangka adalah satu sisi. Tidak syak lagi, semua model trend akan menghasilkan hasil yang baik. Walau bagaimanapun, jika kita memasukkan data pergerakan yang melampau ini ke dalam sampel untuk pengoptimuman parameter, parameter model yang diperoleh tidak semestinya yang terbaik.

Sebagai contoh, jika model mempunyai dua parameter, parameter A mempunyai hasil ujian yang sangat baik pada satu sisi masa berlaku, dan pada masa yang lain ia berfungsi dengan baik; parameter B yang lain mempunyai hasil ujian yang kurang baik pada satu sisi masa berlaku, dan pada masa yang lain ia berfungsi dengan lebih baik daripada parameter A, dan peredaran antara setiap masa adalah sama dengan parameter A. Walaupun parameter A diuji dalam parameter komposit seperti keuntungan risiko lebih tinggi daripada B, kita lebih cenderung untuk memilih parameter B, kerana parameter B adalah lebih stabil dan tidak bergantung pada sampel tertentu.

Ringkasnya, dalam membina model perdagangan berprogram, di satu pihak, model boleh diperbaiki dengan pengoptimuman parameter, supaya model lebih sesuai dengan pola turun naik harga, meningkatkan pulangan pelaburan; dan di sisi lain, untuk mengelakkan penyesuaian berlebihan terhadap pengoptimuman parameter, yang menyebabkan kebolehgunaan model terhadap perubahan keadaan pasaran dikurangkan.

Dipetik daripada Program Trader