Ramalan harga Bitcoin dalam masa nyata menggunakan rangka kerja LSTM

Petua: Kes ini hanya digunakan untuk tujuan penyelidikan dan bukan cadangan pelaburan.

Data harga Bitcoin adalah berdasarkan urutan masa, oleh itu ramalan harga Bitcoin kebanyakan dilakukan menggunakan model LSTM.

Memori jangka pendek panjang (LSTM) adalah model pembelajaran mendalam yang sangat sesuai untuk data siri masa (atau data yang mempunyai urutan masa / ruang / struktur, seperti filem, ayat, dan lain-lain) dan merupakan model ideal untuk meramalkan arah harga mata wang kripto.

Artikel ini adalah mengenai penggabungan data melalui LSTM untuk meramalkan harga masa depan Bitcoin.

import perpustakaan yang diperlukan

import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

Analisis data

Pengisian data

Membaca data perdagangan harian BTC

data = pd.read_csv(filepath_or_buffer="btc_data_day")

Untuk melihat data yang tersedia, terdapat 1380 baris data yang terdiri daripada Data, Open, High, Low, Close, Volume (BTC), Volume (Currency) dan Weighted Price. Selain daripada barisan Data, barisan data lain adalah jenis data float64.

data.info()

Lihat 10 barisan pertama.

data.head(10)

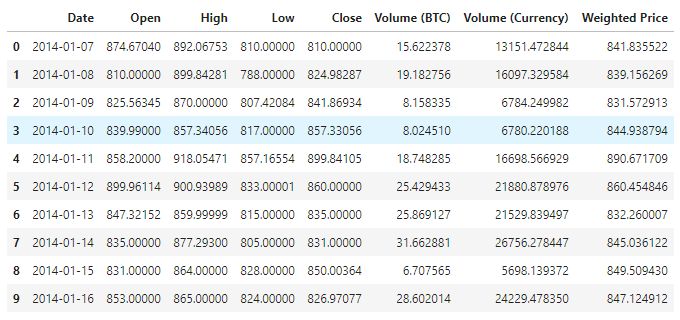
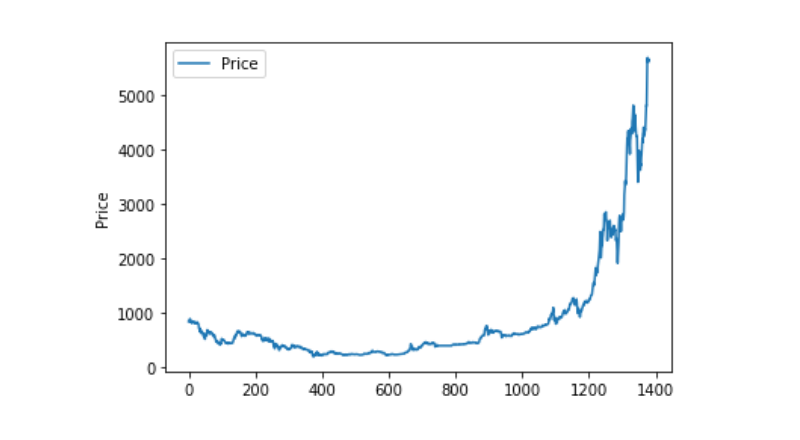
Penglihatan data

Menggunakan matplotlib untuk merangka harga tertimbang untuk melihat pembahagian dan trend data. Dalam gambar, kita mendapati bahagian data 0 yang perlu kita pastikan jika terdapat kecacatan dalam data tersebut.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

Pengolahan data yang luar biasa

Kita lihat jika data itu mengandungi data nan, dan kita boleh lihat bahawa data kita tidak mengandungi data nan.

data.isnull().sum()

Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

Jika kita lihat semula data 0 di bawah, kita boleh lihat bahawa terdapat nilai 0 dalam data kita, dan kita perlu memprosesnya.

(data == 0).astype(int).any()

Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

(data == 0).astype(int).any()

Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

Kemudian lihatlah pembahagian dan pergerakan data, dan pada masa ini, kurva sudah sangat berterusan.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

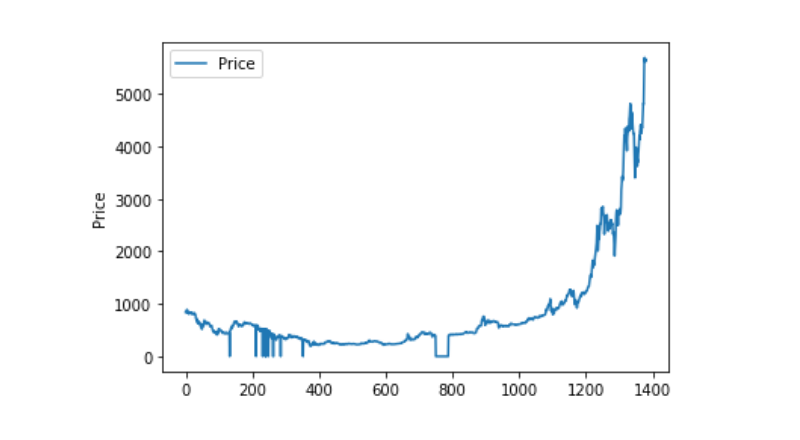
Pemisahan dataset latihan dan dataset ujian

Menggabungkan data kepada 0 - 1

data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

Data kumpulan ujian dan data kumpulan latihan dibagi dengan 2:8.

ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

Membuat set latihan dan set ujian untuk menubuhkan set latihan dan set ujian kami dalam tempoh satu hari sebagai tingkap.

def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Menentukan model dan melatih

Pada kali ini kita menggunakan model yang mudah, yang mempunyai struktur seperti berikut: 1. LSTM2. Dense.

Ini memerlukan penjelasan mengenai bentuk input LSTM. Dimensi input Input Shape adalah batch_size, time steps, features. Di sini, nilai time steps adalah selang waktu tetingkap masa ketika data dimasukkan, di sini kita menggunakan 1 hari sebagai tetingkap masa, dan data kita adalah data hari, jadi di sini langkah masa kita adalah 1.

Memori jangka pendek panjang (Long short-term memory, LSTM) adalah RNN khas yang digunakan untuk menyelesaikan masalah kehilangan gradien dan ledakan gradien semasa latihan siri panjang.

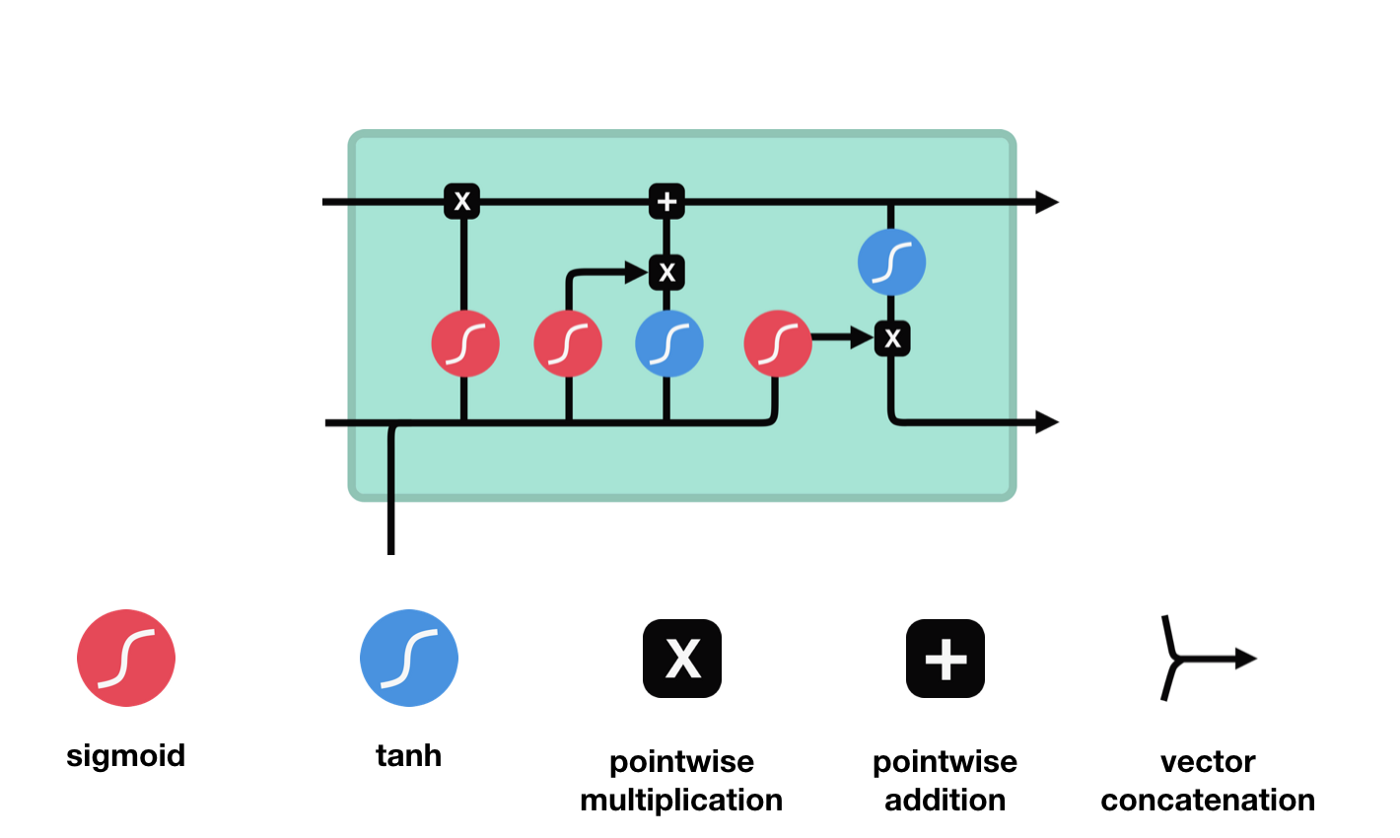
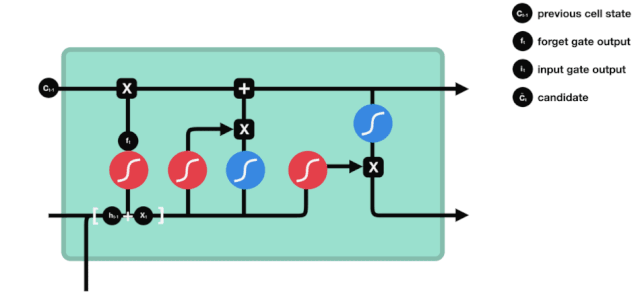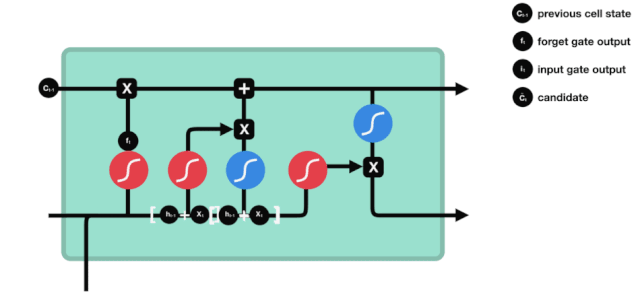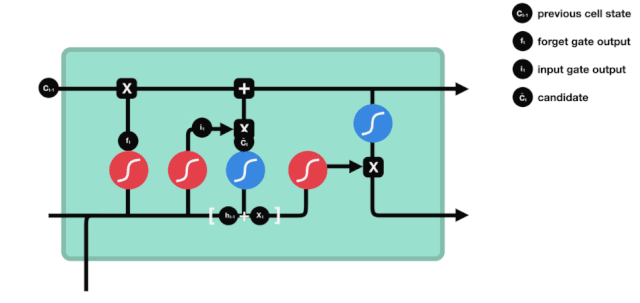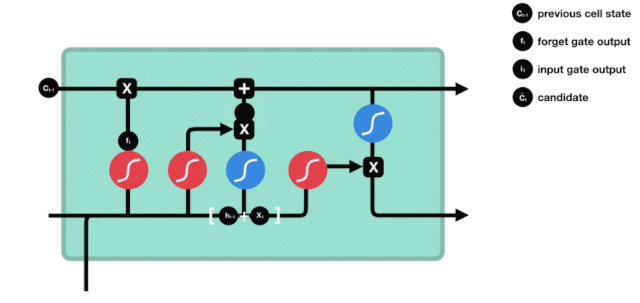
Dari diagram struktur rangkaian LSTM, anda dapat melihat bahawa LSTM sebenarnya adalah model kecil yang mengandungi 3 fungsi pengaktifan sigmoid, 2 fungsi pengaktifan tanh, 3 kali, dan satu penambahan.

Keadaan sel

Status sel adalah pusat LSTM, dia adalah garis hitam di bahagian atas dalam gambar di atas, dan di bawah garis hitam ini adalah beberapa pintu, yang akan kita perkenalkan di kemudian hari. Status sel akan dikemas kini berdasarkan hasil setiap pintu. Di bawah ini, anda akan memahami proses keadaan sel.

Rangkaian LSTM dapat menghapus atau menambah maklumat mengenai keadaan sel melalui struktur yang dikenali sebagai pintu. Pintu boleh memilih keputusan mana maklumat yang akan dilalui. Struktur pintu adalah gabungan lapisan sigmoid dan operasi penggandaan titik. Oleh kerana output lapisan sigmoid adalah nilai 0-1, 0 menandakan tidak boleh dilalui, dan 1 menandakan semua boleh dilalui.

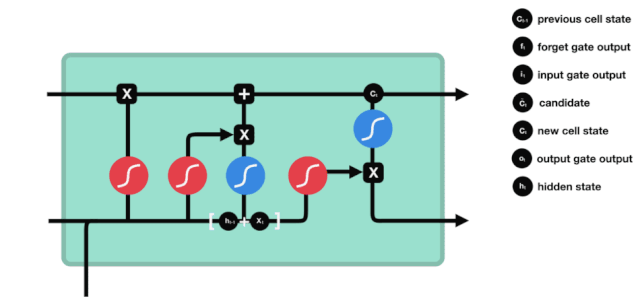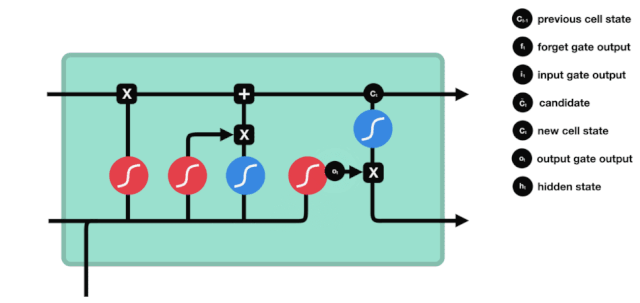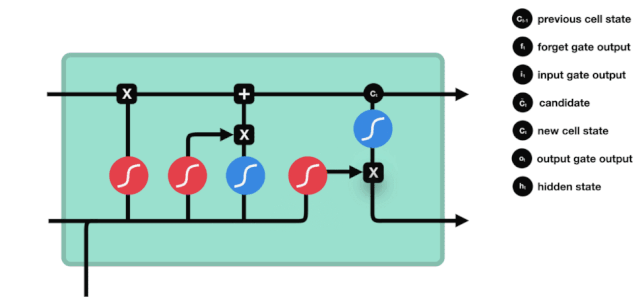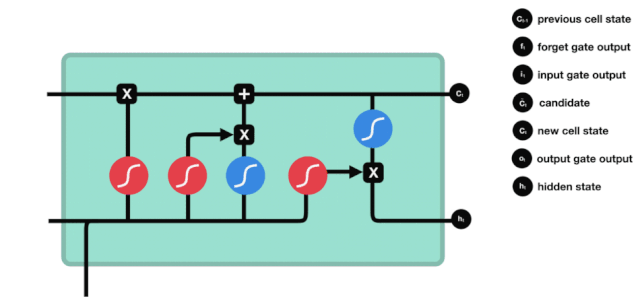
Pintu Lupa

Langkah pertama LSTM adalah untuk menentukan apa maklumat yang perlu dibuang oleh keadaan sel. Bahagian operasi ini dikendalikan oleh unit sigmoid yang dipanggil pintu lupa.

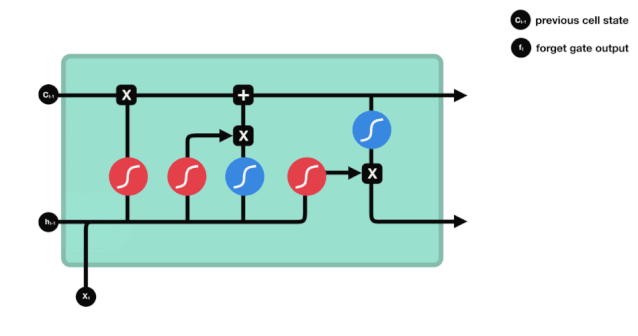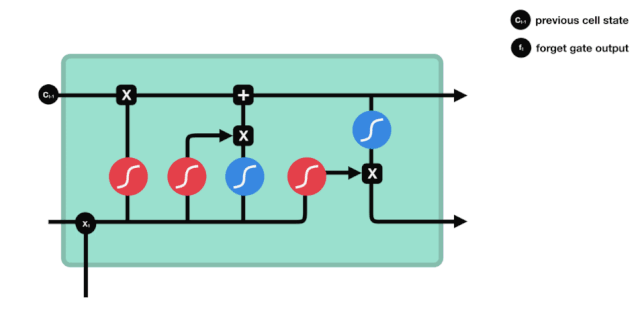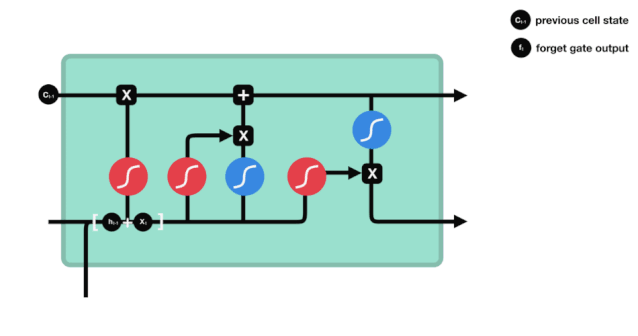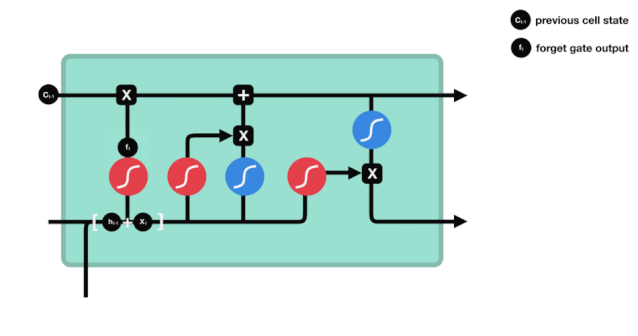
Kita dapat melihat bahawa pintu lupa menghasilkan vektor antara 0-1 dengan melihat maklumat $h_{l-1}$ dan $x_{t}$. Nilai 0-1 dalam vektor ini menunjukkan berapa banyak maklumat yang disimpan atau dibuang dalam keadaan sel $C_{t-1}$. 0 menunjukkan tidak disimpan, dan 1 menunjukkan disimpan.

Ungkapan matematik: $f_{t}=\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right) $

Pintu masuk

Langkah seterusnya adalah memutuskan apa maklumat baru yang akan ditambah kepada keadaan sel, yang dilakukan dengan membuka pintu input.

Kita melihat bahawa maklumat $h_{l-1}$ dan $x_{t}$ dimasukkan ke dalam pintu lupa (sigmoid) dan pintu masuk (tanh). Kerana output pintu lupa adalah nilai 0-1, oleh itu, jika output pintu lupa adalah 0, hasil $C_{i}$ selepas masuk tidak akan ditambahkan ke dalam keadaan sel semasa, jika 1, semuanya akan ditambahkan ke dalam keadaan sel, jadi fungsi pintu lupa di sini adalah untuk memilih untuk menambah hasil pintu masuk ke dalam keadaan sel.

Rumus matematiknya ialah: $C_{t}=f_{t} * C_{t-1} + i_{t} * \tilde{C}_{t} $

Pintu keluar

Selepas kemaskini keadaan sel, ciri-ciri keadaan sel output perlu dipertimbangkan berdasarkan jumlah input $h_{l-1}$ dan $x_{t}$, di mana input perlu melalui lapisan sigmoid yang dikenali sebagai pintu keluar untuk mendapatkan syarat keputusan, dan kemudian keadaan sel melalui lapisan tanh untuk mendapatkan vektor dengan nilai antara -1 ~ 1, yang dikalikan dengan syarat keputusan pintu keluar untuk mendapatkan output unit RNA akhir, seperti yang ditunjukkan di bawah.

def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

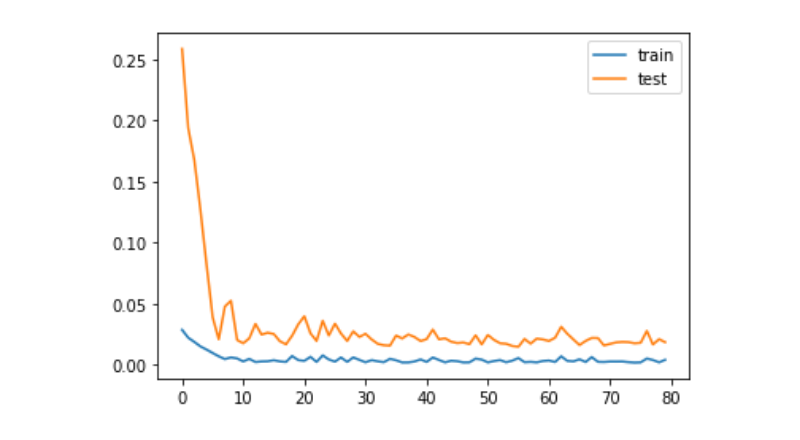
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Ramalan

predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

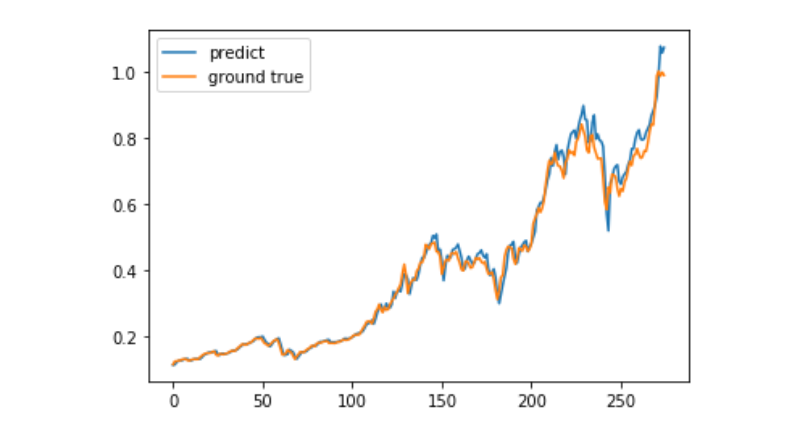
Pada masa ini, ia masih sukar untuk meramalkan pergerakan harga Bitcoin dalam jangka panjang menggunakan pembelajaran mesin, dan artikel ini hanya boleh digunakan sebagai contoh pembelajaran. Kasus ini akan dilancarkan dengan awan matrix dan dalam imej demo, pengguna yang berminat boleh mengalami secara langsung.