Pernyataan hak cipta: Jika anda perlu mengutip kod artikel ini, sila nyatakan sumbernya, jika anda menggunakan untuk tujuan komersil, tulis artikel dengan surat peribadi atau hubungi penulis di 940648114@qq.com

1. Pengenalan

Kelebihan transaksi kuantitatif

Perdagangan kuantitatif merujuk kepada penilaian subjektif manusia yang menggunakan model matematik canggih sebagai pengganti, menggunakan teknologi komputer dari data sejarah yang besar untuk membuat strategi untuk pelbagai insiden kemungkinan besar yang membawa keuntungan yang berlebihan, mengurangkan kesan perubahan emosi pelabur, dan mengelakkan keputusan pelaburan yang tidak rasional dalam keadaan pasaran yang sangat fanatik atau pesimis.           Kerana mata wang digital 24*Keterusan pasaran dagangan 7 jam tanpa henti, dan perdagangan kuantitatif dapat mencapai kesan perdagangan frekuensi tinggi, jelas merupakan permulaan yang baik untuk melakukan kuantiti dari pasaran mata wang digital. Pasaran mata wang digital masih belum matang.

Model GQNR

Model ini adalah berdasarkan model Garch untuk meramalkan kadar lonjakan, menggunakan nilai VaR untuk meramalkan kadar lonjakan melalui pengembalian peratusan dan menggunakan pengembalian bukan linear, seperti GA untuk merangka untuk meramalkan VaR teratas dan VaR terbawah untuk kitaran seterusnya. Model ini disebut GQNR.

Modul Garch 1.

Bahagian ini akan menerangkan secara terperinci mengenai inti strategi Garch, yang mempunyai kebolehgunaan yang meluas di pasaran kewangan dan mencapai kesan ramalan tertentu dalam mata wang digital.

1.1 Definisi Garch

Model ARCH adalah model yang menggunakan urutan kuasa dua sisa yang bergerak pada tahap q untuk menyesuaikan nilai fungsi pemisahan yang berbeza pada masa ini. Oleh kerana model purata bergerak mempunyai pemisahan peringkat q dari faktor korelasi diri, model ARCH sebenarnya hanya sesuai untuk faktor korelasi diri jangka pendek dari fungsi pemisahan diri. Tetapi dalam praktiknya, fungsi perbezaan yang berbeza dengan beberapa urutan sisa adalah bersifat long-term, dan dengan menggunakan fungsi perbezaan yang berbeza yang sesuai dengan model ARCH, ia akan menghasilkan purata bergerak yang tinggi, meningkatkan kesukaran anggaran parameter dan akhirnya mempengaruhi ketepatan yang sesuai dengan model ARCH.                                                                                                                                                                  Model GARCH sebenarnya adalah berdasarkan ARCH, ditambah dengan fungsi pembezaan p yang mempertimbangkan fungsi pembezaan, yang dapat menyesuaikan dengan berkesan fungsi pembezaan dengan memori jangka panjang. Model ARCH adalah contoh khusus model GARCH, model GARCH ((p,q) dengan p = 0).

1.2 Proses ARCH

Definisi σn adalah nilai turun naik aset pada kitaran perdagangan ke-1 pada kitaran perdagangan ke-n, dan mu adalah kadar pulangan harian, maka ia boleh dianggarkan tanpa bias berdasarkan kadar pulangan pada kitaran perdagangan ke-m yang paling baru: $\( \sigma *n^2= \frac{1}{m-1} \sum\limits*{i=1}^m {( { \mu_{n-i}- \overline{\mu} } ) ^2}, \)\(         1 menukar μn-i menjadi kadar pulangan peratusan; 2 menukar m-1 menjadi m; 3 menganggap μ = 0, dan perubahan ini tidak banyak mempengaruhi hasilnya, berdasarkan formula di atas, kadar turun naik dapat disederhanakan menjadi: \)\( \sigma *n^2= \frac{1}{m} \sum\limits*{i=1}^m { \mu_{n-i} ^2}, \)\(         Iaitu, kadar turun naik setiap kitaran mempunyai berat yang sama 1/m, kerana ia adalah anggaran kadar turun naik semasa, data jarak yang lebih dekat harus diberikan berat yang lebih tinggi, maka persamaan di atas boleh diubah menjadi: \)\( \sigma *n^2= \sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)$ αi adalah faktor bagi kadar pulangan kuadrat bagi kitaran dagangan i, mengambil nilai positif dan nilai i yang lebih kecil semakin besar, jumlah beratnya ialah 1 ⋅ lebih jauh lagi, dengan mengandaikan bahawa terdapat sebuah kadar selisih jangka panjang VL, dan beratnya ialah γ, dapat diperoleh berdasarkan formula di atas:

\[ \begin{cases}\sigma *n^2= \gamma V*{L}+\sum\limits_{i=1}^m { \alpha_i\mu_{n-i} ^2}\ &\ \gamma+\sum\limits_{i=1}^m{\alpha_i\mu_{n-i}^2}=1 & \end{cases} , \]

        supayaω = γVL, rumus(15) boleh ditulis semula sebagai: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)\( Dari formula di atas, kita boleh mendapatkan proses ARCH (1) yang biasa. \)\( \sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2}, \)$

1.3 Proses GARCH

Model GARCH ((p,q) adalah gabungan model ARCH ((p) dan EWMA ((q), yang bermaksud bahawa kadar turun naik tidak hanya berkaitan dengan pendapatan sebelum p, tetapi juga berkaitan dengan q, seperti berikut: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}+\sum\limits_{i=1}^m { \beta_i\sigma_{n-i} ^2}, \)\(         Berdasarkan formula di atas, kita boleh mendapatkan GARCH ((1,1)): \)\( \begin{cases}\sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2+\beta\sigma_{n-1}^2}\&\ \qquad\alpha+\beta+\gamma=1 & \end{cases} , \)$

2 Modul QR

Bahagian ini akan menerangkan pengembalian pecahan asas, menggambarkan kepentingan pecahan strategik

2.1 Definisi QR

Pengembalian pecahan adalah kaedah pemodelan untuk menganggarkan hubungan linear antara satu set pembolehubah regresi X dan pecahan pembolehubah Y yang diterangkan. Model pengembalian sebelumnya sebenarnya adalah ekspektasi tertakluk kepada variabel yang diterangkan. Ia juga berkaitan dengan hubungan antara variabel yang diterangkan dan rata-rata peredaran variabel yang diterangkan. Ia mula-mula dikemukakan oleh Koenker dan Bassett pada tahun 1978.

2.2 Dari OLS ke QR

Kaedah regresi umum ialah penggandaan dua terendah, iaitu kuasa dua penjumlahan kesilapan yang diminimumkan: $\( min \sum{({y_i- \widehat{y}*i })}^2 \)\(         dan tujuan peratusan adalah untuk meminimumkan nilai mutlak kesilapan bertimbangan berdasarkan formula di atas dan: \)\( \mathop{\arg\min*\beta}\ \ \sum{[{\tau(y_i-X_i\beta)^++(1-\tau)(X_i\beta-y_i) ^+ }]} \)$

2.2 Visualisasi QR

Seperti yang anda lihat, semua sampel dibahagikan kepada ruang yang berbeza oleh garis regresi, dan garis regresi ini juga menjadi garis pembahagian.

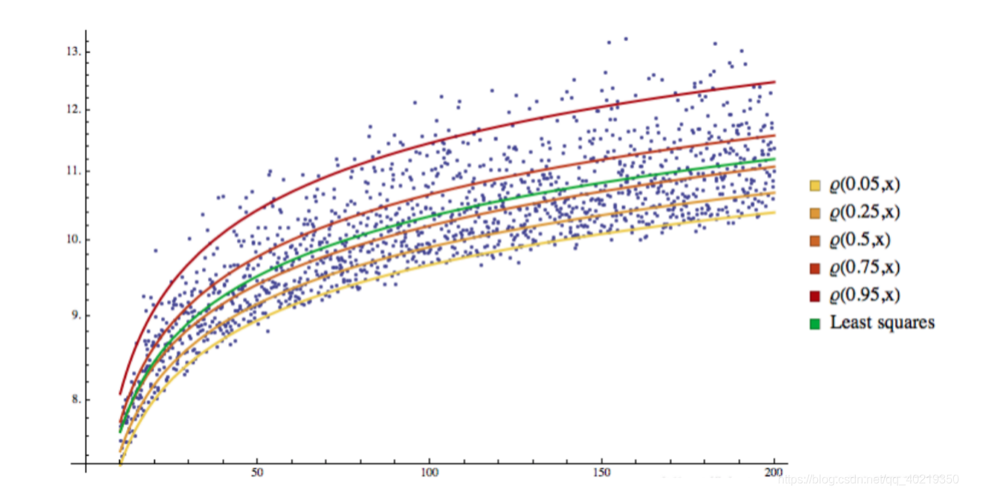
3. Kembalikan GARCH-QR

Kami secara semula jadi berfikir, adakah mungkin untuk menggunakan sigma turun naik pasaran yang tidak diketahui dengan pecahan Q, VaR, untuk membuat pengulangan untuk meramalkan kejatuhan turun naik dalam keadaan kebarangkalian masa depan, sektor ini akan bergerak ke arah ini.

3.1 Pemilihan kadar turun naik dan bentuk pengembalian VaR

        Oleh kerana ini adalah teras strategi, saya akan memberikan satu bentuk untuk menggambarkan pemikiran tersebut. $\( VaR=\epsilon+W^TE\E=(\zeta,\zeta^2,\zeta^3,\zeta^4)\W=(W_1,W_2,W_3,W_4) \)$

3.2 Tentukan fungsi sasaran

Berdasarkan maklumat di atas, kita boleh mendapatkan fungsi sasaran yang akan dioptimumkan: $\( \widehat{W}=\mathop{\arg\min_W}\ \ \sum{[{\alpha(VaR_t-W^TE_t)^++(1-\alpha)(W^TE_t-VaR_t) ^+ }]} \)$

3.3 Menggunakan pembelajaran mesin untuk mengoptimumkan fungsi sasaran

        Langkah ini lebih banyak pilihan, tangga tradisional turun, atau algoritma genetik, pembaca boleh menggunakan kreativiti mereka sendiri untuk bereksperimen.Terdapat alamat algoritma GA

Ketiga, bagaimana menggunakan GQNR dalam kuantitatif

1. Kepastian Idea

Pada setiap titik masa semasa, anda boleh meramalkan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ramalan ram

2. Kesukaran penggunaan

• Mengambil bentuk regresi
• Pilihan algoritma yang boleh disesuaikan
• Parameter pembelajaran mesin yang sesuai
• Ketidakpastian pasaran

3. Penyelesaian

• Memperpendek jangka masa pembelajaran strategi
• Menurunkan risiko jangka panjang dengan deposit tunggal
• Menambah pengesahan bersama trend dua rata-rata dan pengesahan penurunan nilai kedua