Leeks dan penyebaran bid-ask: Kajian awal tentang model EKOP

• 1 Perbincangan Awal

  Bulan-bulan telah berlalu sejak kali terakhir saya menulis di blog ini. Banyak perkara telah berlaku dalam beberapa bulan ini, dan beberapa di antaranya telah menjadi bulan-bulan yang gelap dalam hidup saya sendiri. Tetapi pengalaman ini memberitahu saya bahawa kehidupan, seperti perdagangan, penuh dengan pasang surut dan ketidaktahuan.

  Kita semua tahu bahawa saham yang aktif dalam perdagangan biasanya mempunyai spread yang lebih kecil, dan saham yang tidak aktif dalam perdagangan sebaliknya. Mengapa ini berlaku? Bolehkah anda menggunakan model matematik yang mudah dan cantik untuk menjelaskan perbezaan harga?[[1] Pada mulanya, ia dibentangkan untuk mengkaji apakah tindakan peniaga yang mempunyai maklumat yang berbeza menyebabkan perbezaan harga saham dalam kedua-dua kategori. Dalam artikel ini, saya akan memperkenalkan asas model ini.

• 2 Asumsi Proses Perdagangan

  Apabila kita bercakap tentang model kewangan, yang paling penting adalah memberi perhatian kepada hipotesis model tersebut. Model kewangan yang baik mempunyai hipotesis yang sesuai: ia tidak akan terlalu kuat sehingga tidak dapat digunakan secara umum; ia tidak akan terlalu lemah sehingga tidak dapat menghasilkan hasil yang ringkas dan cantik.

  Hipotesis 1: Kami membincangkan perdagangan saham, perdagangan berlaku pada hari-hari yang berpecah-belah, hipotesis berterusan sepanjang hari. Iaitu, perdagangan pedagang berlaku pada 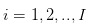hari-hari perdagangan yang berpecah-belah. Dan dalam hari perdagangan, perdagangan berlaku pada 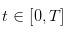pada masa berturut-turut seperti itu.

  • Berita buruknya, kami mencatat nilai saham sebagai
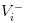
  • Berita baiknya, kami mencatatkan nilai saham sebagai
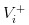
  • Tiada berita berlaku, kami mencatat nilai saham sebagai

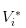
  Jelas sekali, kita mempunyai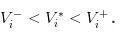

  Hipotesis 2: Pada suatu hari, terdapat α

  Kebarangkalian berlaku peristiwa yang mempengaruhi harga saham, ada kebarangkalian 1-α yang tidak berlaku peristiwa yang mempengaruhi harga saham. Pada hari kejadian berlaku, ada kebarangkalianδ yang berlaku yang akan menyebabkan harga saham turun, dan ada kebarangkalianδ yang berlaku yang akan menyebabkan harga saham naik.

  Hipotesis 3: Peserta dalam perdagangan saham terdiri daripada pembuat pasaran (market maker, disingkat MM), peniaga yang berpengetahuan (informed trader, disingkat IT), dan peniaga yang tidak berpengetahuan (uninformed trader, disingkat UT). Mereka masing-masing mematuhi tingkah laku perdagangan seperti berikut:

  MM sentiasa bersedia untuk menaikkan satu unit pembelian atau penjualan, melakukan kewajiban sebagai seorang peniaga pasaran. MM adalah neutral risiko, oleh itu harga yang dia tawarkan adalah harga yang adil menurutnya sendiri.

  IT hanya berdagang pada hari-hari berita berlaku, tingkah laku mereka adalah proses santai. Pada suatu hari, jika ada berita buruk, dia akan memasang satu tiket jual dengan kadar kedatangan μ; dan pada hari-hari yang berlaku berita baik, dia akan memasang satu pembelian dengan kadar kedatangan μ.

  UT, iaitu orang miskin kita, kerana mereka tidak mempunyai maklumat, mereka melakukan transaksi dengan cara yang tidak teratur, setiap hari mereka melakukan pembelian dan penjualan dengan kadar yang sesuai.
  Perhatikan bahawa kesemua proses Poson di sini adalah saling bebas. Kita boleh menggambarkan hipotesis 3 dengan satu grafik, seperti berikut:

  

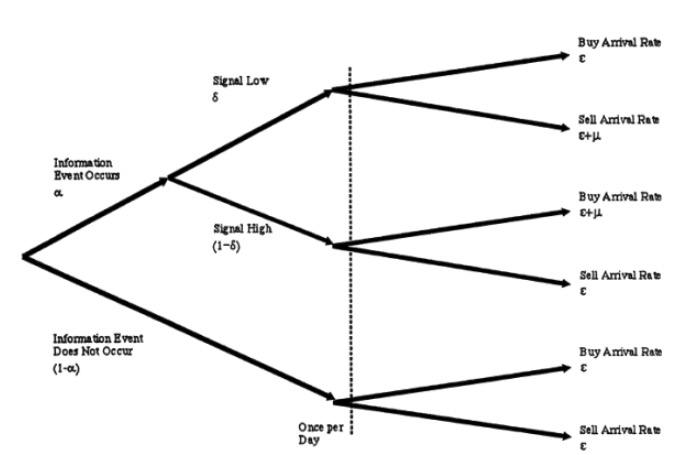
• 3 Kemas kini transaksi dan harga

  Kita tahu bahawa peniaga pasaran biasanya bekerja untuk syarikat besar yang bekerja keras. Mereka sangat pintar, dan dalam perjuangan mereka dengan IT dan IT dalam jangka masa yang panjang, mereka telah mengumpul semua parameter model dalam diagram pokok di atas melalui analisis data sejarah yang besar. Namun, mereka tidak begitu hebat seperti peniaga yang berpengetahuan, dan ketika hari perdagangan akan bermula, mereka tidak seperti peniaga yang berpengetahuan, tidak tahu sama ada sesuatu yang penting telah berlaku pada hari ini.

  Sekarang, marilah kita bereksperimen dengan MM, berhadapan dengan IT dan UT. Pada satu titik waktu t, kita memaparkan diri kita sebagai sebuah vektor untuk meneka kemungkinan sesuatu yang tidak berlaku, sesuatu yang baik dan sesuatu yang buruk.

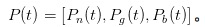  。 Jelas sekali, pada hari yang baru bermula, iaitu pada hari /upload/asset/7a5565722b92d2accf331f58923d6bab702659de.png, saya tidak melihat satu pun laporan, jadi yang saya boleh katakan adalah bahawa kemungkinan tidak berlaku adalah α, kemungkinan yang baik adalah /upload/asset/c9cf50c6146a25c662c593ed229845822bfac7a5.png, dan kemungkinan yang buruk adalah /upload/asset/87418f07b12fce65f4c3f70b024e94d2e19f769a.png.

  Bagaimana untuk mengemas kini kebarangkalian ini? Baiklah, kita semua yang melakukan pilihan pasaran tahu formula Bayes. Apabila kita melihat satu tawaran yang datang, kita menggunakan hukum Bayes untuk mengemas kini anggaran kebarangkalian kita.

  

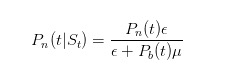
  Formula ini bermolekul untuk mengatakan bahawa hanya peniaga yang tidak tahu akan menjual dengan nilai ε apabila tidak ada berita; dan pembahagian untuk mengatakan bahawa pada bila-bila masa, peniaga yang tidak tahu akan menjual dengan nilai ε, dan peniaga yang tahu akan menjual dengan nilai μ apabila sesuatu yang buruk berlaku.

  

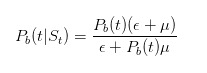
  dan

  

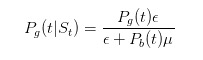
  Sebelum kita teruskan, mari kita buat beberapa ujian mudah. Kita cakap, jika kita nampak satu tiket, kita patut besarkan peluang untuk sesuatu yang buruk berlaku.

  

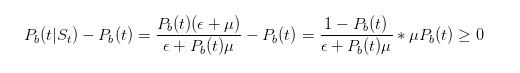
  Oleh itu, anda dapat melihat bahawa deduksi kami mengesahkan intuisi kami.

  Dengan probabiliti yang diperbaharui, kita boleh mengira harga yang adil sebagai harga beli yang kita buat dalam pasaran, yang dinyatakan sebagai

  

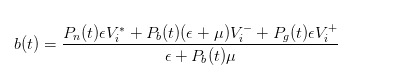
  Melalui kesimpulan yang sama, kita dapat melihat bahawa apabila pesanan untuk membeli datang, harga jual yang kita laporkan sebagai penjual haruslah

  

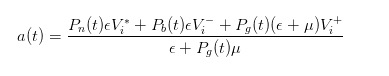
• 4 Ungkapan perbezaan harga selepas perubahan harga

  Perkataan harga beli dan harga jual di atas tidak cukup intuitif, kita boleh memasukkan nilai yang diharapkan untuk saham pada masa t untuk mempermudahkan percakapan.

  

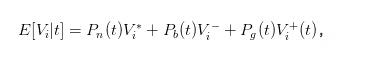
  Jadi, kita boleh menukarkan bid dan ask ke

  

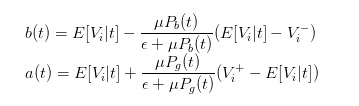
  Oleh itu, kita boleh menyatakan perbezaan harga dengan jelas sebagai

  

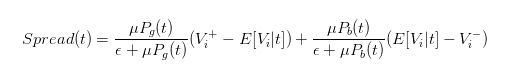
• 5 Kesan tingkah laku peniaga terhadap perbezaan harga

  Dengan ungkapan perbezaan harga, kita dapat menganalisis kesan perbezaan harga yang berlaku di kalangan peniaga yang berbeza.

  Semakin banyak ketupat, semakin kecil perbezaan harga. Perhatikan, ε adalah kadar penyampaian peniaga yang tidak tahu (biarlah kita panggil mereka ketupat ketupat), dan jika ε >> μ, kita dapat melihat, / upload/asset/539e0cfb1aae368277dd0e3840448b6a39abd087.png Kedua-duanya akan mendekati 0, yang bermaksud bahawa penyebaran juga akan mendekati 0.
  Jika kita pergi ke ekstrem yang lain, andaikan di pasaran tidak ada sawit, hanya ada sekumpulan peniaga yang lebih mahir daripada sawit, maka kita akan mendapati dengan malang, harga yang kita letakkan akan menjadi 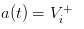dan /upload/asset/1248ca7d3d472490982c9d0aa7b2e04b51269b18.png, jadi peniaga yang berpengetahuan mendapati diri mereka tidak menguntungkan untuk membeli atau menjual, pasaran pasti akan mati.

  Anda lihat, kita boleh membuat kesimpulan yang menarik dan mendalam berdasarkan beberapa andaian, menggunakan deduksi matematik yang sangat mudah, dan ini mungkin daya tarikan besar model matematik. Selepas membaca artikel ini, saya juga berharap anda boleh bersikap baik terhadap ketupat, kita ketupat adalah jaminan pasaran untuk berdagang dengan normal!

[1] Easley, David, et al. "Liquidity, information, and infrequently traded stocks." The Journal of Finance 51.4 (1996): 1405-1436.