Alat yang ampuh untuk peniaga programatik: Algoritma Kemas kini Inkremental untuk Mengira purata dan varians

Pengantar

Dalam perdagangan berprogram, sering kali perlu mengira purata dan varians, seperti mengira purata bergerak dan penunjuk turun naik. Apabila kita memerlukan pengiraan frekuensi tinggi dan jangka panjang, perlu menyimpan data sejarah untuk masa yang lama, yang tidak perlu dan memakan sumber. Artikel ini memperkenalkan algoritma kemas kini dalam talian untuk mengira purata dan varians bertimbang, yang sangat penting untuk memproses aliran data masa nyata dan menyesuaikan secara dinamik strategi perdagangan, terutamanya strategi frekuensi tinggi. Artikel ini juga menyediakan pelaksanaan kod Python yang sesuai untuk membantu peniaga dengan cepat menggunakan dan menggunakan algoritma dalam perdagangan sebenar.

Purata dan Varians Sederhana

Jika kita menggunakan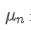untuk mewakili nilai purata titik data ke-n, dengan mengandaikan bahawa kita telah mengira purata titik data n-1 /upload/asset/28e28ae0beba5e8a810a6.png, sekarang kita menerima titik data baru /upload/asset/28d4723cf4cab1cf78f50.png. Kita mahu mengira bilangan purata baru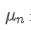termasuk titik data baru. Berikut adalah hasil yang terperinci.

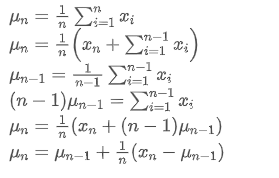
Proses kemas kini varians boleh dibahagikan kepada langkah-langkah berikut:

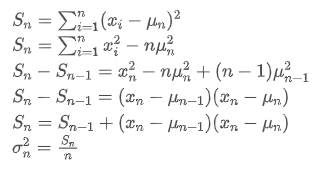
Seperti yang dapat dilihat dari dua formula di atas, proses ini membolehkan kita untuk mengemas kini purata baru dan varians apabila menerima setiap titik data baru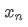dengan hanya mengekalkan purata dan varians data sebelumnya, tanpa menyimpan data sejarah, membuat pengiraan lebih cekap. Walau bagaimanapun, masalahnya adalah bahawa apa yang kita kira dengan cara ini adalah purata dan varians semua sampel, sementara dalam strategi sebenar, kita perlu mempertimbangkan tempoh tetap tertentu. Mengamati kemas kini purata di atas menunjukkan bahawa jumlah kemas kini purata baru adalah penyimpangan antara data baru dan purata masa lalu dikalikan dengan nisbah. Jika nisbah ini ditetapkan, ia akan membawa kepada purata bertimbang eksponensial, yang akan kita bincangkan seterusnya.

Purata yang ditimbang secara eksponensial

Purata bertingkat eksponensial boleh ditakrifkan oleh hubungan rekursif berikut:

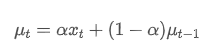
Antara mereka,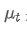ialah purata bertimbang eksponen pada titik masa t,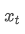ialah nilai yang diperhatikan pada titik masa t, α adalah faktor berat, dan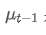adalah purata bertimbang eksponen dari titik masa sebelumnya.

Varian yang diberi berat secara eksponen

Berkenaan dengan varians, kita perlu mengira purata berat eksponensial penyimpangan kuadrat pada setiap titik masa. Ini boleh dicapai melalui hubungan rekursif berikut:

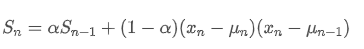
Antara mereka,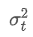ialah varian bertimbang eksponen pada titik masa t, dan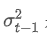adalah varians berimbang eksponen dari titik masa sebelumnya.

Memerhatikan purata dan varians yang ditimbang secara eksponensial, kemas kini tambahan mereka adalah intuitif, mengekalkan sebahagian daripada nilai masa lalu dan menambah perubahan baru.https://fanf2.user.srcf.net/hermes/doc/antiforgery/stats.pdf

SMA dan EMA

SMA (juga dikenali sebagai purata aritmetik) dan EMA adalah dua langkah statistik biasa, masing-masing dengan ciri dan kegunaan yang berbeza. Yang pertama menetapkan berat yang sama kepada setiap pemerhatian, mencerminkan kedudukan pusat set data. Yang terakhir adalah kaedah pengiraan rekursif yang memberikan berat yang lebih tinggi kepada pemerhatian yang lebih baru. Berat menurun secara eksponensial kerana jarak dari masa semasa meningkat untuk setiap pemerhatian.

• Pengedaran berat: SMA memberikan berat yang sama kepada setiap titik data, manakala EMA memberikan berat yang lebih tinggi kepada titik data yang paling baru.
• Sensitiviti terhadap maklumat baru: SMA tidak cukup sensitif terhadap data yang baru ditambah, kerana ia melibatkan pengiraan semula semua titik data.
• Kerumitan pengiraan: Pengiraan SMA agak mudah, tetapi apabila bilangan titik data meningkat, begitu juga kos pengiraan. Pengiraan EMA lebih kompleks, tetapi kerana sifatnya yang berulang, ia dapat mengendalikan aliran data berterusan dengan lebih cekap.

Kaedah penukaran kira-kira Antara EMA dan SMA

Walaupun SMA dan EMA berbeza secara konseptual, kita boleh membuat EMA kira-kira kepada SMA yang mengandungi bilangan pemerhatian tertentu dengan memilih nilai α yang sesuai.

SMA adalah purata aritmetik semua harga dalam tetingkap masa tertentu. Untuk tetingkap masa N, centroid SMA (iaitu kedudukan di mana nombor purata terletak) boleh dianggap sebagai:

pusat SMA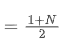

EMA adalah jenis purata tertimbang di mana titik data yang paling baru mempunyai berat yang lebih besar. Berat EMA menurun secara eksponensial dari masa ke masa.

pusat EMA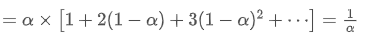

Apabila kita menganggap bahawa SMA dan EMA mempunyai centroid yang sama, kita boleh mendapatkan:

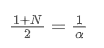
Untuk menyelesaikan persamaan ini, kita boleh mendapatkan hubungan antara α dan N.

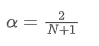
Ini bermaksud bahawa untuk SMA N hari yang diberikan, nilai α yang sepadan boleh digunakan untuk mengira EMA setara, supaya mereka mempunyai centroid yang sama dan hasilnya sangat serupa.

Penukaran EMA dengan kekerapan kemas kini yang berbeza

Misalkan kita mempunyai EMA yang dikemas kini setiap saat, dengan faktor berat /upload/asset/28da19ef219cae323a32f.png. Ini bermaksud bahawa setiap saat, titik data baru akan ditambahkan ke EMA dengan berat /upload/asset/28da19ef219cae323a32f.png, sementara pengaruh titik data lama akan dikalikan dengan /upload/asset/28cfb008ac438a12e1127.png.

Jika kita mengubah kekerapan kemas kini, seperti kemas kini sekali setiap f saat, kita mahu mencari faktor berat baru /upload/asset/28d2d28762e349a03c531.png, supaya kesan keseluruhan titik data dalam f saat adalah sama seperti apabila dikemas kini setiap saat.

Dalam tempoh f saat, jika tiada kemas kini dibuat, kesan titik data lama akan terus merosot f kali, setiap kali dikalikan dengan /upload/asset/28e50eb9c37d5626d6691.png. Oleh itu, jumlah faktor merosot selepas f saat adalah /upload/asset/28e296f97d8c8344a2ee6.png.

Untuk membuat EMA dikemas kini setiap f saat mempunyai kesan kerosakan yang sama dengan EMA dikemas kini setiap saat dalam satu tempoh kemas kini, kita menetapkan jumlah faktor kerosakan selepas f saat sama dengan faktor kerosakan dalam satu tempoh kemas kini:

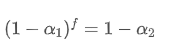
Menyelesaikan persamaan ini, kita mendapat faktor berat baru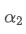

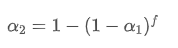
Rumus ini memberikan nilai purata faktor berat baru /upload/asset/28d2d28762e349a03c531.png, yang mengekalkan kesan pelemahan EMA tidak berubah apabila kekerapan kemas kini berubah.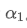dengan nilai 0.001 dan mengemas kini setiap 10 saat, jika ia ditukar kepada kemas kini setiap saat, nilai bersamaan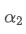adalah kira-kira 0.01.

Pelaksanaan Kod Python

class ExponentialWeightedStats:
    def __init__(self, alpha):
        self.alpha = alpha
        self.mu = 0
        self.S = 0
        self.initialized = False

    def update(self, x):
        if not self.initialized:
            self.mu = x
            self.S = 0
            self.initialized = True
        else:
            temp = x - self.mu
            new_mu = self.mu + self.alpha * temp
            self.S = self.alpha * self.S + (1 - self.alpha) * temp * (x - self.mu)
            self.mu = new_mu

    @property
    def mean(self):
        return self.mu

    @property
    def variance(self):
        return self.S

# Usage example
alpha = 0.05  # Weight factor
stats = ExponentialWeightedStats(alpha)
data_stream = [] # Data stream
for data_point in data_stream:
    stats.update(data_point)

Ringkasan

Dalam perdagangan berprogram frekuensi tinggi, pemprosesan data masa nyata yang cepat adalah penting. Untuk meningkatkan kecekapan pengiraan dan mengurangkan penggunaan sumber, artikel ini memperkenalkan algoritma kemas kini dalam talian untuk terus mengira purata tertimbang dan varians aliran data. Kemas kini tambahan masa nyata juga boleh digunakan untuk pelbagai pengiraan data statistik dan penunjuk, seperti korelasi antara dua harga aset, pemasangan linear, dan lain-lain, dengan potensi yang besar. Kemas kini tambahan memperlakukan data sebagai sistem isyarat, yang merupakan evolusi dalam pemikiran berbanding pengiraan tempoh tetap.