Statistik Bayesian ialah disiplin yang berkuasa dalam matematik dengan aplikasi meluas dalam banyak bidang, termasuk kewangan, penyelidikan perubatan dan teknologi maklumat. Ia membolehkan kami menggabungkan kepercayaan terdahulu dengan bukti untuk mencapai kepercayaan posterior baharu, membolehkan kami membuat keputusan yang lebih termaklum.

Dalam artikel ini, kami akan memperkenalkan secara ringkas beberapa ahli matematik utama yang mengasaskan bidang ini.

Sebelum Bayes Untuk lebih memahami statistik Bayesian, kita perlu kembali ke abad ke-18 dan merujuk kepada ahli matematik De Moivre dan karyanya “The Principle of Chance”[1]。

Dalam risalahnya, De Moivre menangani banyak masalah pada zamannya yang berkaitan dengan kebarangkalian dan perjudian. Seperti yang anda ketahui, penyelesaiannya kepada salah satu masalah ini membawa kepada asal-usul taburan normal, tetapi itu cerita lain.

Dalam kertas kerjanya ada soalan mudah:

“Kebarangkalian mendapat tiga kepala apabila melambung syiling adil tiga kali berturut-turut.”

Membaca masalah yang diterangkan dalam “Prinsip Peluang”, anda mungkin perasan bahawa kebanyakan masalah itu bermula dengan hipotesis dari mana kebarangkalian peristiwa tertentu dikira. Sebagai contoh, dalam masalah di atas, terdapat andaian bahawa syiling adalah adil, jadi kebarangkalian untuk mendapat kepala dalam lambungan ialah 0.5.

Ini dinyatakan dalam istilah matematik hari ini sebagai:

𝑃(𝑋|𝜃)

Tetapi bagaimana jika kita tidak tahu sama ada syiling itu adil? Jika kita tidak tahu𝜃Kain bulu?

Thomas Bayes dan Richard Price

Hampir lima puluh tahun kemudian, pada tahun 1763, sebuah kertas bertajuk “An Essay on the Principle of Chance”[2] Diterbitkan dalam Philosophical Transactions of the Royal Society of London.

Dalam beberapa muka surat pertama dokumen itu, terdapat teks yang ditulis oleh ahli matematik Richard Price, meringkaskan kandungan kertas yang ditulis oleh rakannya Thomas Bayes beberapa tahun sebelum kematiannya. Dalam pengenalan, Price menerangkan kepentingan beberapa penemuan yang dibuat oleh Thomas Bayes yang tidak diliputi dalam Prinsip Peluang De Moivre.

Malah, dia merujuk kepada masalah tertentu:

“Memandangkan bilangan kejadian dan kegagalan peristiwa yang tidak diketahui, cari peluang kejadiannya berada di antara mana-mana dua darjah kebarangkalian yang dinamakan.”

Dalam erti kata lain, selepas memerhatikan sesuatu peristiwa, kita dapati parameter yang tidak diketahuiθApakah kebarangkalian antara dua darjah kebarangkalian? Ini sebenarnya adalah salah satu masalah pertama dalam sejarah yang berkaitan dengan inferens statistik, dan menimbulkan nama kebarangkalian songsang. Dari segi matematik:

𝑃( 𝜃 | 𝑋）

Ini sudah tentu apa yang hari ini kita panggil pengedaran posterior teorem Bayes.

Punca yang tidak bersebab

Kenali dua pendeta tua ini.Thomas BayesdanRichard Harga, apa yang mendorong penyelidikan sebenarnya sangat menarik. Tetapi untuk melakukan ini, kita perlu mengetepikan sedikit pengetahuan tentang statistik untuk seketika.

Kita berada di abad ke-18, dan kebarangkalian menjadi bidang yang semakin diminati oleh ahli matematik. Ahli matematik seperti De Moivre atau Bernoulli telah menunjukkan bahawa beberapa kejadian berlaku dengan tahap rawak tertentu tetapi masih dikawal oleh peraturan tetap. Sebagai contoh, jika anda melempar dadu berkali-kali, satu daripada enam kali ia akan mendarat di atas enam. Seolah-olah ada peraturan tersembunyi yang menentukan nasib peluang.

Sekarang, bayangkan anda seorang ahli matematik dan penganut yang taat yang hidup dalam tempoh ini. Anda mungkin berminat untuk mengetahui bagaimana peraturan tersembunyi ini berkaitan dengan Tuhan.

Ini memang soalan yang Bayes dan Price sendiri tanya. Penyelesaian yang mereka harapkan untuk menyelesaikan masalah ini secara langsung boleh digunakan untuk membuktikan bahawa “dunia mestilah hasil kebijaksanaan dan kepintaran; dengan itu memberikan bukti kewujudan Tuhan sebagai sebab terakhir”[2] - Maksudnya, tiada sebab dan akibat.

Laplace

Anehnya, kira-kira dua tahun kemudian, pada tahun 1774, nampaknya tanpa membaca kertas Thomas Bayes, ahli matematik Perancis Laplace menulis kertas bertajuk “Mengenai Punca Peristiwa melalui Kebarangkalian Peristiwa”.[3], iaitu kertas tentang masalah kebarangkalian songsang. Pada halaman pertama anda boleh membaca

Prinsip utama ialah:

“Jika sesuatu peristiwa boleh disebabkan oleh n sebab yang berbeza, maka kebarangkalian punca-punca ini untuk peristiwa tertentu adalah dalam nisbah yang sama dengan kebarangkalian kejadian yang diberi sebab, dan kebarangkalian kewujudan setiap punca ini adalah sama. kepada kebarangkalian kejadian yang diberi sebab Kebarangkalian sebab-sebab, dibahagikan dengan jumlah kebarangkalian kejadian yang diberikan setiap sebab tersebut.

Inilah yang kita ketahui hari ini sebagai teorem Bayes:

​

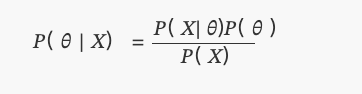
dalamP(θ)diedarkan secara seragam.

Eksperimen Syiling

Kami akan membawa statistik Bayesian ke masa kini dengan menggunakan Python dan perpustakaan PyMC dan melakukan eksperimen mudah.

Katakan seorang rakan memberi anda syiling dan bertanya kepada anda sama ada anda fikir ia adalah syiling yang adil. Kerana dia tergesa-gesa, dia memberitahu anda untuk membalikkan syiling 10 kali sahaja. Seperti yang anda lihat, terdapat parameter yang tidak diketahui dalam masalah inip, kebarangkalian mendapat kepala dalam lambungan syiling, dan kami ingin menganggarkan inipNilai yang paling mungkin .

(Nota: Kami tidak bercakap tentang parameterpialah pembolehubah rawak, tetapi parameter ini ditetapkan dan kami ingin tahu antara nilai yang paling mungkin. ）

Untuk mendapatkan perspektif yang berbeza tentang masalah ini, kami akan menanganinya di bawah dua kepercayaan terdahulu yang berbeza:

• 1. Anda tidak mempunyai maklumat terdahulu tentang kesaksamaan syiling dan memberikan kebarangkalian yang sama kepadap. Dalam kes ini, kami akan menggunakan apa yang dipanggil prior tidak bermaklumat, kerana anda tidak menambah sebarang maklumat pada kepercayaan anda.
• 1. Anda tahu dari pengalaman bahawa walaupun syiling mungkin tidak adil, sukar untuk menjadikannya sangat tidak adil, jadi anda fikir parameternyapIa kemungkinan besar tidak akan turun di bawah 0.3 atau di atas 0.7. Dalam kes ini, kami akan menggunakan maklumat terdahulu.

Untuk kedua-dua kes, kepercayaan terdahulu kami adalah seperti berikut:

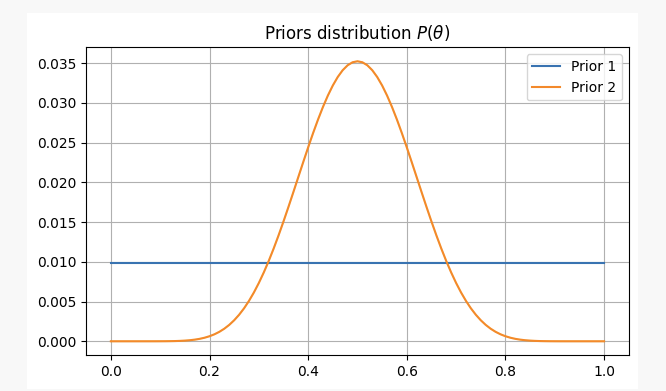
Selepas melambung syiling 10 kali, anda mendapat 2 kepala. Dengan bukti ini, kita mungkin boleh memikirkan tempat untuk mencari parameter kitap？

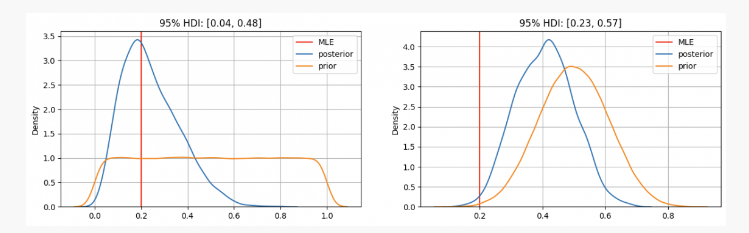
Seperti yang anda lihat, dalam kes pertama kita adapPengagihan sebelumnya adalah berpusat pada anggaran kemungkinan maksimum (MLE)p=0.2, iaitu pendekatan yang sama menggunakan kaedah frequentist. Parameter yang tidak diketahui sebenar akan terletak dalam selang 95% yang boleh dipercayai antara 0.04 dan 0.48.

Sebaliknya, apabila terdapat keyakinan yang tinggi bahawa parameterp Sedangkan ia sepatutnya antara 0.3 dan 0.7, kita dapat melihat bahawa taburan posterior adalah sekitar 0.4, yang jauh lebih tinggi daripada nilai yang diberikan oleh MLE kita. Dalam kes ini, parameter yang tidak diketahui sebenar akan terletak dalam selang 95% yang boleh dipercayai antara 0.23 dan 0.57.

Jadi dalam kes pertama, anda akan memberitahu rakan anda bahawa anda yakin syiling itu tidak adil. Tetapi dalam kes lain, anda akan memberitahunya bahawa anda tidak pasti sama ada syiling itu adil.

Seperti yang anda lihat, walaupun dengan bukti yang sama (2 kepala daripada 10 lambungan), keputusan boleh berbeza memandangkan kepercayaan terdahulu yang berbeza. Ini adalah kekuatan statistik Bayesian, yang, sama dengan kaedah saintifik, membolehkan kami mengemas kini kepercayaan kami dengan menggabungkan kepercayaan terdahulu dengan pemerhatian dan bukti baharu.

END

Dalam artikel hari ini, kami melihat asal usul statistik Bayesian dan penyumbang utamanya. Sejak itu, terdapat banyak lagi penyumbang penting dalam bidang statistik ini (Jeffreys, Cox, Shannon, dll.), diterbitkan semula daripada quantdare.com.