Bayes - Menjelaskan Misteri Kebarangkalian, Meneroka Kebijaksanaan Matematik di Balik Keputusan

Statistik Bayesian adalah disiplin yang kuat dalam bidang matematik, dengan aplikasi yang luas di banyak bidang termasuk kewangan, penyelidikan perubatan, dan teknologi maklumat.

Dalam artikel ini, kita akan memperkenalkan secara ringkas beberapa ahli matematik utama yang mengasaskan bidang ini.

Sebelum Bayes Untuk lebih memahami statistik Bayesian, kita perlu kembali ke abad ke-18 dan merujuk kepada ahli matematik De Moivre dan makalahnya The Doctrine of Chances.

Dalam karyanya, De Moivre menyelesaikan banyak masalah yang berkaitan dengan kebarangkalian dan perjudian pada zamannya.

Salah satu soalan yang paling mudah dalam kertas kerja beliau adalah:

Berapakah kebarangkalian mendapat tiga kepala apabila melemparkan duit syiling adil tiga kali berturut-turut?

Membaca melalui masalah yang diterangkan dalam The Doctrine of Chances, anda mungkin melihat bahawa kebanyakan bermula dengan andaian dari mana mereka mengira kebarangkalian untuk peristiwa tertentu.

Ini akan dinyatakan hari ini dalam istilah matematik sebagai:

Rumus

𝑃(𝑋|𝜃)

Namun, bagaimana jika kita tidak tahu sama ada duit syiling itu adil?𝜃 ?

Thomas Bayes dan Richard Price

Hampir lima puluh tahun kemudian, pada tahun 1763, kertas berjudul A Solusi kepada Masalah dalam Doktrin Kesempatan diterbitkan dalam Transaksi Filosofis Persatuan Diraja London.

Dalam beberapa halaman pertama dokumen ini, terdapat satu karya yang ditulis oleh ahli matematik Richard Price yang meringkaskan kertas kerja yang ditulis oleh rakannya Thomas Bayes beberapa tahun sebelum kematiannya.

Malah, dia merujuk kepada satu masalah khusus:

Berikutan peristiwa yang tidak diketahuijumlah kejayaan dan kegagalan, cari peluang antara dua darjah yang dinamakan.

Dalam erti kata lain, selepas memerhatikan peristiwa kita menentukan apa yang kebarangkalian bahawa parameter yang tidak diketahuiθIni sebenarnya salah satu masalah pertama yang berkaitan dengan kesimpulan statistik dalam sejarah dan ia menimbulkan istilah kebarangkalian terbalik.

Rumus

𝑃( 𝜃 | 𝑋）

Ini adalah apa yang kita panggil sebaran posterior teorema Bayes hari ini.

Untuk Alasan Tanpa Penyebab dan Kesan

Memahami motivasi di sebalik penyelidikan kedua-dua menteri tua ini,Thomas BayesdanRichard Price, sebenarnya agak menarik. Tetapi untuk melakukan ini, kita perlu untuk sementara masa mengesampingkan beberapa pengetahuan mengenai statistik.

Kita berada di abad ke-18 ketika kebarangkalian menjadi bidang yang semakin menarik bagi ahli matematik. Ahli matematik seperti de Moivre atau Bernoulli telah menunjukkan bahawa beberapa peristiwa berlaku dengan tahap rawak tertentu tetapi masih diatur oleh peraturan tetap. Sebagai contoh, jika anda melempar dadu beberapa kali, satu perenam masa ia akan mendarat di enam. Seolah-olah ada peraturan tersembunyi yang menentukan peluang nasib.

Sekarang bayangkan anda seorang ahli matematik dan seorang yang beriman hidup pada zaman ini. anda mungkin berminat untuk memahami hubungan antara peraturan tersembunyi ini dan Tuhan.

Ini memang soalan yang ditanya oleh Bayes dan Price sendiri. Mereka berharap bahawa penyelesaian mereka akan secara langsung digunakan untuk membuktikan dunia mestilah hasil kebijaksanaan dan kecerdasan; oleh itu memberikan bukti untuk kewujudan Tuhan sebagai sebab utama - iaitu, sebab tanpa sebab.

Laplace

Anehnya, kira-kira dua tahun kemudian pada tahun 1774, tanpa membaca kertas Thomas Bayes, ahli matematik Perancis Laplace menulis kertas berjudul On the Causes of Events by Probability of Events, yang mengenai masalah kebarangkalian terbalik.

Jika suatu peristiwa boleh disebabkan oleh n sebab yang berbeza, maka nisbah antara sebab-sebab ini kebarangkalian yang diberikan kepada peristiwa sama dengan kebarangkalian peristiwa yang diberikan kepada sebab-sebab ini; dan setiap sebab kemungkinan kewujudan sama dengan kebarangkalian sebab-sebab yang diberikan kepada peristiwa ini dibahagikan dengan jumlah kebarangkalian peristiwa yang diberikan kepada setiap sebab ini.

Inilah yang kita tahu hari ini sebagai teorema Bayes:

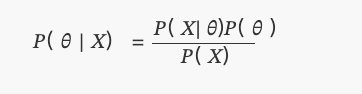
Di mana?P(θ)adalah sebaran seragam.

Percubaan Koin

Kami akan membawa statistik Bayesian kepada masa kini dengan menggunakan Python dan perpustakaan PyMC, dan menjalankan eksperimen yang mudah.

Misalkan seorang kawan memberi anda duit syiling dan bertanya jika anda fikir ia adalah duit syiling yang adil. kerana dia tergesa-gesa, dia memberitahu anda bahawa anda hanya boleh melemparkan duit syiling 10 kali. seperti yang anda lihat, terdapat parameter yang tidak diketahuipdalam masalah ini, yang merupakan kebarangkalian mendapat kepala dalam membuang syiling, dan kita mahu menganggarkan nilai yang paling mungkinp.

(Catatan: Kami tidak mengatakan bahawa parameterpadalah pembolehubah rawak tetapi sebaliknya parameter ini tetap; kita mahu tahu di mana ia adalah paling mungkin antara.)

Untuk mempunyai pandangan yang berbeza mengenai masalah ini, kita akan menyelesaikannya di bawah dua kepercayaan terdahulu yang berbeza:

• 1. Anda tidak mempunyai maklumat terlebih dahulu mengenai keadilan duit syiling, jadi anda menetapkan kebarangkalian yang sama kepadapDalam kes ini, kita akan menggunakan apa yang dipanggil sebelum tidak bermaklumat kerana anda tidak menambah sebarang maklumat kepada kepercayaan anda.
• 2. Dari pengalaman anda, anda tahu bahawa walaupun duit syiling mungkin tidak adil, ia adalah sukar untuk menjadikannya sangat tidak adil.padalah tidak mungkin kurang daripada 0.3 atau lebih daripada 0.7. dalam kes ini, kita akan menggunakan sebelum informatif.

Untuk kedua-dua senario ini, kepercayaan kami akan seperti berikut:

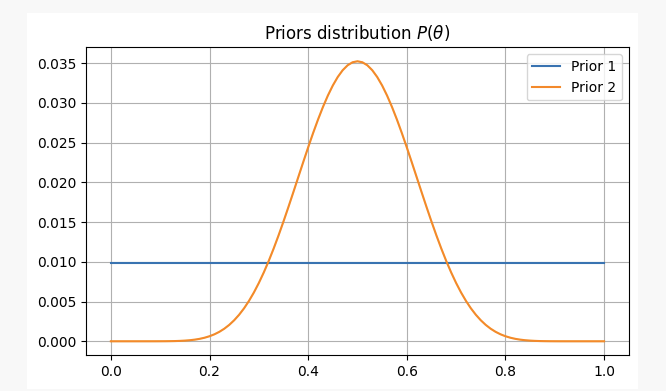
Dengan bukti ini, di mana kita boleh mencari parameterp?

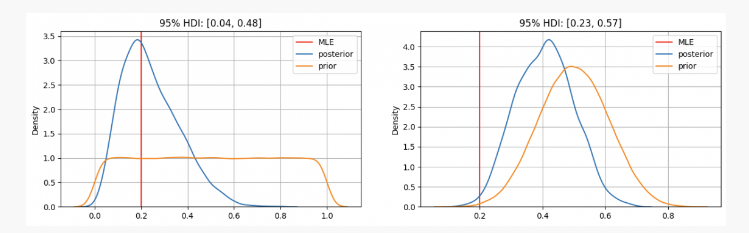
Seperti yang anda lihat, dalam kes pertama, pembahagian parameter kami sebelumnyaptertumpu pada anggaran kebarangkalian maksimum (MLE)p=0.2, yang merupakan kaedah yang serupa dengan yang digunakan oleh sekolah frekuensi. parameter yang tidak diketahui benar akan berada dalam selang kepastian 95%, antara 0.04 dan 0.48.

Sebaliknya, dalam kes-kes di mana terdapat keyakinan yang tinggi bahawa parameterpJika parameter yang tidak diketahui adalah antara 0.3 dan 0.7, kita dapat melihat bahawa pengedaran posterior adalah sekitar 0.4, jauh lebih tinggi daripada apa yang diberikan oleh MLE kita.

Oleh itu, dalam senario kes pertama anda akan memberitahu rakan anda dengan pasti bahawa duit syiling ini tidak adil tetapi dalam situasi lain anda akan mengatakan ia tidak pasti sama ada ia adil atau tidak.

Seperti yang anda lihat walaupun menghadapi bukti yang sama (dua kepala daripada sepuluh dilemparkan), di bawah kepercayaan sebelumnya yang berbeza hasil boleh berbeza-beza; satu kelebihan statistik Bayesian berbanding kaedah tradisional terletak di sini: seperti metodologi saintifik ia membolehkan kita mengemas kini kepercayaan kita dengan menggabungkannya dengan pemerhatian dan bukti baru.

END

Dalam artikel hari ini, kita melihat asal-usul statistik Bayesian dan penyumbang utamanya.quantdare.com.