Pengisihan FMEX membuka kunci pengoptimuman kuantiti pesanan yang optimum
 0
0
 2177
2177

Kejatuhan FMEX menyebabkan banyak masalah kepada ramai orang, tetapi baru-baru ini ia menghasilkan pelan mulakan semula dan merumuskan peraturan yang serupa dengan perlombongan asal untuk membuka kunci hutang. Artikel analisis telah diberikan mengenai perlombongan transaksi: https://www.fmz.com/bbs-topic/5834. Terdapat juga ruang untuk pengoptimuman dalam menyusun perlombongan. Walaupun orang ramai tidak sepatutnya jatuh ke dalam lubang yang sama dua kali, mereka yang mempunyai tuntutan mengenai FMEX mungkin ingin merujuknya Strategi masa nyata khusus yang boleh dijalankan pada platform kuantitatif FMZ juga boleh dikeluarkan.
Peraturan buka kunci pengisihan FMEX
Tentukan setiap 5 minit setiap hari sebagai kitaran buka kunci pengisihan, dan setiap kitaran diperuntukkan 1⁄288 daripada kuota buka kunci pengisihan pasangan transaksi pada hari tersebut. Dalam setiap kitaran, titik masa rawak dipilih untuk mengambil gambar pesanan beli dan jual pasangan dagangan, di mana:
- Beli 1 Berdasarkan perkadaran jumlah pesanan pengguna, 1⁄4 daripada jumlah pulangan tempoh buka kunci diperuntukkan kepada kedudukan ini
- Jual 1 Mengikut perkadaran jumlah pesanan pengguna, 1⁄4 daripada jumlah pulangan tempoh buka kunci diperuntukkan kepada kedudukan ini
- Untuk 4 peringkat belian 2 untuk beli 5, 1⁄40 daripada jumlah pulangan tempoh buka kunci akan diperuntukkan kepada setiap peringkat mengikut perkadaran jumlah pesanan pengguna dalam setiap peringkat.
- Untuk pesanan dalam 4 peringkat jual 2 hingga jual 5, 1⁄40 daripada jumlah pulangan tempoh buka kunci kedudukan akan diperuntukkan mengikut perkadaran jumlah pesanan pengguna dalam setiap peringkat.
- Untuk lima pesanan daripada Beli 6 hingga Beli 10, 1⁄50 daripada jumlah pulangan tempoh buka kunci akan diperuntukkan kepada setiap pesanan mengikut perkadaran jumlah pesanan dalam setiap pesanan.
- Untuk lima peringkat pesanan jualan dari 6 hingga 10, 1⁄50 daripada jumlah pulangan tempoh buka kunci akan diperuntukkan kepada setiap peringkat mengikut perkadaran jumlah pesanan pengguna dalam setiap peringkat.
- Untuk lima pesanan daripada Beli 11 hingga Beli 15, 1⁄100 daripada jumlah pulangan tempoh buka kunci akan diperuntukkan kepada setiap pesanan mengikut perkadaran jumlah pesanan dalam setiap pesanan.
- Untuk lima pesanan daripada Jual 11 hingga Jual 15, 1⁄100 daripada jumlah pulangan tempoh buka kunci akan diperuntukkan kepada setiap pesanan mengikut perkadaran jumlah pesanan dalam setiap pesanan.
Jumlah pulangan pembuka kunci kedudukan pengguna dalam pasangan dagangan tertentu pada hari yang sama ialah jumlah amaun yang dikembalikan kepada pengguna untuk pembuka kunci kedudukan dalam setiap kitaran pasangan dagangan.
Isih untuk membuka kunci faedah
Pertama, jumlah pendapatan pengisihan dan buka kunci ialah:
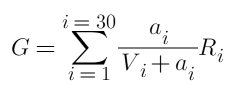
Di sini, i mewakili salah satu jawatan, terdapat 30 jawatan secara keseluruhan untuk kedua-dua pihak, a ialah kuantiti pesanan belum selesai, R ialah jumlah pulangan membuka kunci, dan V ialah jumlah pesanan sedia ada.
Tidak seperti membuka kunci transaksi, membuat pesanan tidak mempunyai kos Di sini, R hanya perlu mempertimbangkan saiz relatif, dan tidak perlu mempertimbangkan jumlah mutlak yang dinyatakan dalam USDT. Jika kita menentukan jumlah pesanan belum selesai, persoalannya ialah bagaimana untuk memperuntukkan pesanan ke kedudukan yang berbeza untuk memaksimumkan keuntungan G. Hanya mencari lokasi dengan kuantiti pesanan terkecil dan membuat semua pesanan di sana jelas bukan penyelesaian yang optimum. Sebagai contoh, terdapat tiga posisi dengan 10 pesanan sedia ada, dan R mereka adalah sama Kami menetapkan jumlah pesanan kepada 30. Jika kita hanya memilih satu kedudukan untuk membuat pesanan, jumlah keuntungan akhir ialah 0.75R keuntungan akhir ialah 1.5R, yang menunjukkan bahawa kadangkala keuntungan pesanan tersebar adalah lebih baik. Jadi bagaimana anda memperuntukkan dana?
Pengoptimuman pengisihan membuka kunci
Akhir sekali, objektif dan kekangan pengoptimuman kami ialah:
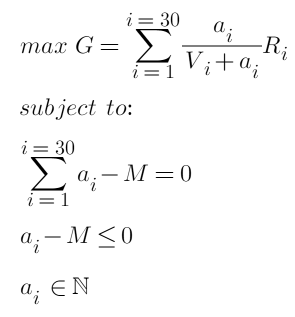
Di mana M ialah jumlah kuantiti pesanan. Ini ialah masalah pengoptimuman cembung kuadratik yang melibatkan ketaksamaan, yang memenuhi syarat KTT dan mempunyai penyelesaian integer. Menggunakan pakej yang sepadan dan penyelesai pengoptimuman cembung, adalah mungkin untuk mendapatkan hasil secara langsung dan mengembalikan kuantiti pesanan yang optimum untuk setiap kedudukan. Tetapi ini jelas bukan jawapan yang kita mahukan. Kita perlu memudahkan masalah dan mendapatkan langkah penyelesaian khusus.
Mari kita mulakan dengan contoh mudah
Pertimbangkan hanya dua peringkat Jumlah pesanan semasa ialah 10 dan 20 (masing-masing dirujuk sebagai peringkat pertama dan peringkat kedua Kuota buka kuncinya ialah R. Jumlah pesanan rizab strategi ialah 30. Bagaimanakah ia harus diperuntukkan? Adakah had pembuka kunci dana telah dimaksimumkan? Soalan ini nampak mudah, tetapi sukar untuk membuat kesimpulan yang betul tanpa pengiraan Pembaca mungkin ingin memikirkan jawapannya terlebih dahulu.
Senario 1:
Cari kedudukan pesanan minimum dan letakkan semua pesanan di sana, jumlah keuntungan G=30/(30+10)=0.75R. Ini juga merupakan penyelesaian yang paling mudah untuk difikirkan.
Senario 2:
1 yuan diperuntukkan setiap kali dan diperuntukkan kepada tempat yang boleh menjana keuntungan terbesar, iaitu tempat yang mempunyai bilangan pesanan belum selesai terkecil. Kemudian yuan pertama akan diperuntukkan kepada peringkat pertama, dan jumlah pesanan peringkat pertama akan menjadi 10+1 Yuan kedua juga akan diperuntukkan kepada peringkat pertama… dan seterusnya, sehingga sejumlah 10 yuan. diperuntukkan kepada peringkat pertama Pada masa ini, Satu akan dipilih secara rawak, dan apabila jumlah pesanan belum selesai dalam peringkat pertama melebihi 20, ia akan diperuntukkan kepada peringkat kedua. Keputusan akhir ialah 20 yuan diperuntukkan kepada peringkat pertama dan 10 yuan diperuntukkan kepada peringkat kedua, dan pesanan terakhir mereka adalah kedua-duanya 30. Jumlah keuntungan G=20⁄30+10⁄30=R. Penyelesaian ini jauh lebih baik daripada Penyelesaian 1 dan juga lebih mudah untuk dikira.
Penyelesaian 3:
Kita boleh mengandaikan bahawa peringkat pertama diperuntukkan a, dan peringkat kedua ialah 30-a Kemudian kita boleh menyenaraikan secara langsung persamaan dan mencari terbitannya sebagai 0 (proses tidak disenaraikan di sini, ia serupa dengan artikel mengenai membuka kunci transaksi. ), dan hitung hasil akhir Formulanya ialah:
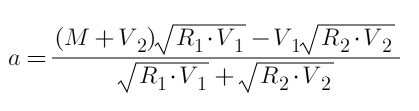
Gantikan dalam integer dan dapatkan a=15. Jumlah keuntungan G=15⁄25+15⁄35=1.0286R, yang lebih baik daripada Pilihan 2. Memandangkan ia diperoleh secara langsung daripada formula, ini adalah penyelesaian yang optimum.
Hasilnya mungkin berbeza daripada apa yang anda jangkakan. Jelas sekali bahawa peruntukan setiap dolar dalam Pelan 2 adalah penyelesaian optimum dalam keadaan semasa. Situasi ini sangat biasa. Matlamat kami untuk setiap langkah pengoptimuman adalah untuk memaksimumkan kecekapan keseluruhan dan bukannya memaksimumkan manfaat tunggal.
Pelan pengoptimuman khusus
Akhirnya, kami telah memulakan operasi sebenar yang boleh dilaksanakan. Mari permudahkan masalah dengan memperuntukkan 1 yuan setiap kali. Mula-mula, mari kita ukur kecekapan Derivatif boleh mencerminkan sumbangan setiap a kepada G. Sumbangan ini mengambil kira kos kumulatif dan bukannya faedah satu pengagihan Jelas sekali, mengikut graf fungsi, apabila a=1, kecekapan adalah yang tertinggi daripada kewujudan kepada ketiadaan, dan kemudian berkurangan secara beransur-ansur.
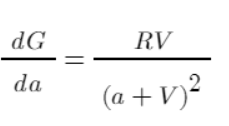
Mengambil contoh mudah di atas sebagai contoh, kita boleh mengira kecekapan peruntukan dana mereka dan menyenaraikannya dalam jadual:
| dana | 1 | 2 |
|---|---|---|
| 1 | 0.0826 | 0.0454 |
| 2 | 0.069 | 0.0413 |
| 3 | 0.0592 | 0.0378 |
| 4 | 0.051 | 0.0347 |
| 5 | 0.0444 | 0.032 |
| … | … | … |
|12 | 0.0207 |0.0195| |13 | 0.0189 |0.0184| |14 | 0.0174 |0.0173| |15 | 0.016 |0.0163| |16 | 0.0148 |0.0154| |17 | 0.0137 |0.0146| |18 | 0.0128 |0.0139|
Mengikut jadual, yuan pertama diperuntukkan kepada peringkat pertama, yuan kedua diperuntukkan kepada peringkat pertama… yuan kelima diperuntukkan kepada peringkat kedua… dan seterusnya, dan akhirnya 15 yuan diperuntukkan kepada peringkat pertama dan 15 yuan ke peringkat kedua, yang merupakan penyelesaian optimum yang kami kira berdasarkan persamaan. Khusus untuk gear ke-30, algoritma adalah sama, dan langkah-langkah khusus ialah:
- 1. Periksa semua gear dahulu Jika V=0, maka a=1, dan tiada lagi dana akan diperuntukkan.
- 2. Agihkan jumlah dana kepada N bahagian, dan pilih gear untuk peruntukan setiap kali.
- 3. Kira kecekapan setiap gear = RV/pow(a+V,2), di mana a mewakili dana terkumpul yang diperuntukkan kepada kedudukan + dana yang diperuntukkan kali ini.
- 4. Peruntukkan dana kepada gear yang paling cekap, dan pilih satu secara rawak jika kecekapan adalah sama.
- 5. Ulang 3-4 sehingga dana diperuntukkan
Jika jumlah pesanan kami adalah besar, adalah terlalu tidak cekap untuk memperuntukkan setiap dolar pada satu masa Kami boleh membahagikan dana kepada 100 bahagian dan memperuntukkan satu bahagian pada satu masa Memandangkan ia hanya pengiraan dan pengisihan yang mudah, algoritmanya adalah sangat cekap. Khususnya pada peringkat pelaksanaan, masih ada ruang untuk pengoptimuman, seperti membahagikan pesanan kami kepada 100, supaya setiap kali kami membuat pelarasan, kami hanya perlu mengagihkan semula pesanan dan bukannya membatalkan semuanya. Anda juga boleh menetapkan nilai R sendiri dan memberi lebih berat kepada mereka yang jauh dari pasaran Jika terdapat pertindihan antara buka kunci jenis dan buka kunci pesanan belum selesai, anda boleh mempertimbangkannya bersama-sama, dan seterusnya.
Artikel ini ialah artikel asal daripada Platform Kuantitatif FMZ Sila nyatakan sumber apabila memindahkan: https://www.fmz.com/bbs-topic-new/5843.