Pemodelan dan Analisis Volatiliti Bitcoin Berdasarkan Model ARMA-EGARCH

Baru-baru ini, saya telah membuat beberapa analisis mengenai turun naik Bitcoin, yang bersuara dan spontan. Jadi saya hanya berkongsi beberapa pemahaman dan kod saya seperti berikut. Keupayaan saya terhad, dan kodnya tidak begitu sempurna. Jika ada kesilapan, sila tunjukkan dan betulkan secara langsung.

1. Penerangan ringkas mengenai siri masa kewangan

Siri masa kewangan adalah satu set model siri Proses Stochastic berdasarkan pembolehubah yang diperhatikan dalam dimensi masa. pembolehubah biasanya adalah kadar pulangan aset. Kerana kadar pulangan bebas dari skala pelaburan dan mempunyai sifat statistik, lebih berharga untuk menganalisis peluang pelaburan aset kewangan yang mendasari.

Di sini, dengan berani diasumsikan bahawa kadar pulangan Bitcoin mematuhi ciri kadar pulangan aset kewangan umum, iaitu, ia adalah siri yang lemah halus, yang dapat ditunjukkan dengan ujian konsistensi beberapa sampel.

Persediaan, perpustakaan import, fungsi pembungkus

Konfigurasi persekitaran penyelidikan selesai. Perpustakaan yang diperlukan untuk pengiraan seterusnya diimport di sini. Oleh kerana ia ditulis secara berkala, ia mungkin berlebihan. Sila bersihkan sendiri.

Dalam [1]:

'''
start: 2020-02-01 00:00:00
end: 2020-03-01 00:00:00
period: 1h
exchanges: [{"eid":"Huobi","currency":"BTC_USDT","stocks":0}]
'''
from __future__ import absolute_import, division, print_function
from fmz import * # Import all FMZ functions
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.graphics.api import qqplot
from statsmodels.stats.diagnostic import acorr_ljungbox as lb_test
from scipy import stats
from arch import arch_model
from datetime import timedelta
from itertools import product
from math import sqrt
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error

task = VCtx(__doc__) # Initialization, verification of FMZ reading of historical data
print(exchange.GetAccount())

Keluar[1]: {Balan : 10000.0, FrozenBalan : 0.0, Stok : 0.0, FrozenStocks : 0.0}

    #### Encapsulate some of the functions, which will be used later. If there is a source, see the note

Dalam [17]:

# Plot functions
def tsplot(y, y_2, lags=None, title='', figsize=(18, 8)):  # source code: https://tomaugspurger.github.io/modern-7-timeseries.html
    fig = plt.figure(figsize=figsize)
    layout = (2, 2)
    ts_ax   = plt.subplot2grid(layout, (0, 0))
    ts2_ax = plt.subplot2grid(layout, (0, 1))
    acf_ax  = plt.subplot2grid(layout, (1, 0))
    pacf_ax = plt.subplot2grid(layout, (1, 1))
    y.plot(ax=ts_ax)
    ts_ax.set_title(title)
    y_2.plot(ax=ts2_ax)
    smt.graphics.plot_acf(y, lags=lags, ax=acf_ax)
    smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax)
    [ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
    sns.despine()
    plt.tight_layout()
    return ts_ax, ts2_ax, acf_ax, pacf_ax

# Performance evaluation
def get_rmse(y, y_hat):
    mse = np.mean((y - y_hat)**2)
    return np.sqrt(mse)

def get_mape(y, y_hat):
    perc_err = (100*(y - y_hat))/y
    return np.mean(abs(perc_err))

def get_mase(y, y_hat):
    abs_err = abs(y - y_hat)
    dsum=sum(abs(y[1:] - y_hat[1:]))
    t = len(y)
    denom = (1/(t - 1))* dsum
    return np.mean(abs_err/denom)

def mae(observation, forecast):    
    error = mean_absolute_error(observation, forecast)
    print('Mean Absolute Error (MAE): {:.3g}'.format(error))
    return error

def mape(observation, forecast): 
    observation, forecast = np.array(observation), np.array(forecast)
    # Might encounter division by zero error when observation is zero
    error = np.mean(np.abs((observation - forecast) / observation)) * 100
    print('Mean Absolute Percentage Error (MAPE): {:.3g}'.format(error))
    return error

def rmse(observation, forecast):
    error = sqrt(mean_squared_error(observation, forecast))
    print('Root Mean Square Error (RMSE): {:.3g}'.format(error))
    return error

def evaluate(pd_dataframe, observation, forecast):
    first_valid_date = pd_dataframe[forecast].first_valid_index()
    mae_error = mae(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    mape_error = mape(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    rmse_error = rmse(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ]) 

    ax = pd_dataframe.loc[:, [observation, forecast]].plot(figsize=(18,5))
    ax.xaxis.label.set_visible(False)
    return

Mari kita mulakan dengan pemahaman ringkas mengenai data sejarah Bitcoin

Dari sudut pandang statistik, kita boleh melihat beberapa ciri data Bitcoin. Mengambil penerangan data tahun lalu sebagai contoh, kadar pulangan dikira dengan cara yang mudah, iaitu harga penutupan dikurangkan logaritma. Formula adalah seperti berikut: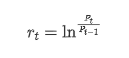

Dalam [3]:

df = get_bars('huobi.btc_usdt', '1d', count=10000, start='2019-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
mean = btc_year_test.mean()
std = btc_year_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value'], columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% btc_year_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% btc_year_test.kurt())
normal_result

Keluar[3]: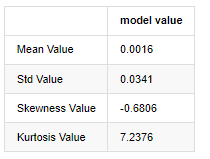

Ciri ekor lemak tebal ialah semakin pendek skala masa, semakin signifikan ciri tersebut. kurtosis akan meningkat dengan peningkatan kekerapan data, dan ciri ini akan sangat jelas dalam data frekuensi tinggi.

Mengambil data harga penutupan harian dari 1 Januari 2019 hingga sekarang sebagai contoh, kami membuat analisis deskriptif kadar pulangan logaritma, dan dapat dilihat bahawa siri kadar pulangan sederhana Bitcoin tidak sesuai dengan pengagihan normal, dan ia mempunyai ciri jelas ekor lemak tebal.

Nilai purata urutan adalah 0.0016, penyimpangan standard adalah 0.0341, kesesuaian adalah -0.6819, dan kurtosis adalah 7.2243, yang jauh lebih tinggi daripada pengedaran normal dan mempunyai ciri ekor lemak tebal. normaliti kadar pulangan mudah Bitcoin diukur dan diuji dengan carta QQ seperti berikut:

Dalam [4]:

fig = plt.figure(figsize=(4,4))
ax = fig.add_subplot(111)
fig = qqplot(btc_year_test['log_return'], line='q', ax=ax, fit=True)

Keluar[4]:

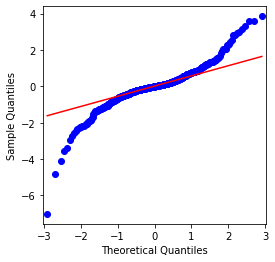
Ia dapat dilihat bahawa carta QQ adalah sempurna, dan siri pulangan logaritma untuk Bitcoin tidak sesuai dengan pengedaran normal dari hasil, dan ia mempunyai ciri jelas ekor lemak tebal.

Seterusnya, mari kita lihat kesan agregasi turun naik, iaitu, siri masa kewangan sering disertai dengan turun naik yang lebih besar selepas turun naik yang lebih besar, sementara turun naik yang lebih kecil biasanya diikuti oleh turun naik yang lebih kecil.

Kluster Volatiliti mencerminkan kesan maklum balas positif dan negatif dari volatiliti dan ia sangat berkaitan dengan ciri ekor lemak. Secara ekonomi, ini menunjukkan bahawa siri masa volatiliti mungkin autocorrelated, iaitu, volatiliti tempoh semasa mungkin mempunyai beberapa hubungan dengan tempoh sebelumnya, tempoh sebelumnya kedua, atau bahkan tempoh sebelumnya ketiga.

Dalam [5]:

df = get_bars('huobi.btc_usdt', '1d', count=50000, start='2006-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
sns.mpl.rcParams['figure.figsize'] = (18, 4)  # Volatility
ax1 = btc_year_test['log_return'].plot()
ax1.xaxis.label.set_visible(False)

Keluar[5]:

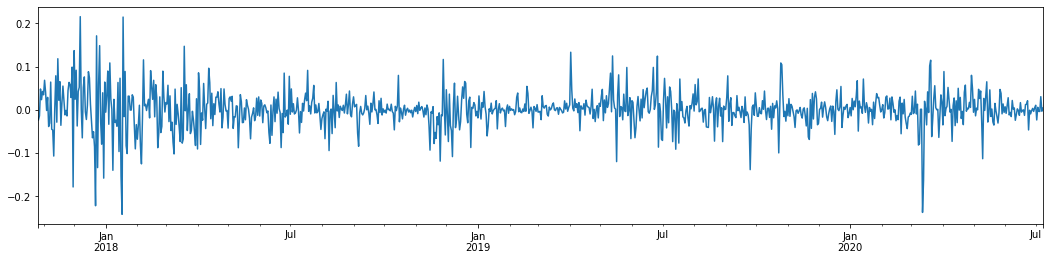
Jika kita mengambil kadar pulangan logaritma harian Bitcoin dalam 3 tahun yang lalu dan memetakannya, fenomena kluster volatiliti dapat dilihat dengan jelas. Selepas pasaran lembu di Bitcoin pada tahun 2018, ia berada dalam kedudukan yang stabil untuk sebahagian besar masa. Seperti yang dapat kita lihat di sebelah kanan, pada bulan Mac 2020, ketika pasaran kewangan global runtuh, terdapat juga aliran ke likuiditi Bitcoin, dengan pulangan merosot hampir 40% dalam sehari, dengan perubahan negatif yang tajam.

Secara ringkas, dari pemerhatian intuitif, kita dapat melihat bahawa turun naik yang besar akan diikuti oleh turun naik padat dengan kebarangkalian yang besar, yang juga merupakan kesan agregasi turun naik.

1-3. Penyediaan data

Untuk menyediakan set sampel latihan, pertama, kita menubuhkan sampel penanda aras, di mana kadar pulangan logaritma adalah volatiliti yang diperhatikan yang setara.

Kaedah pengambilan semula sampel adalah berdasarkan data setiap jam.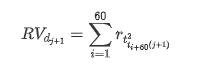

Dalam [4]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_all = pd.DataFrame(df['close'], dtype=np.float)
kline_all.index.name = 'date'
kline_all['log_price'] = np.log(kline_all['close'])  # Calculate daily logarithmic rate of return
kline_all['return'] = kline_all['log_price'].pct_change().dropna()
kline_all['log_return'] = kline_all['log_price'] - kline_all['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_all['squared_log_return'] = np.power(kline_all['log_return'], 2)  # The exponential square of logarithmic daily rate of return

kline_all['return_100x'] = np.multiply(kline_all['return'], 100)
kline_all['log_return_100x'] = np.multiply(kline_all['log_return'], 100)  # Enlarge 100 times

kline_all['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy()  # Resampling to days
kline_all['realized_volatility_1_hour'] = np.sqrt(kline_all['realized_variance_1_hour'])  # Volatility of variance derivation

kline_all = kline_all[4:-29] # Remove the last line because it is missing
kline_all.head(3)

Keluar[4]: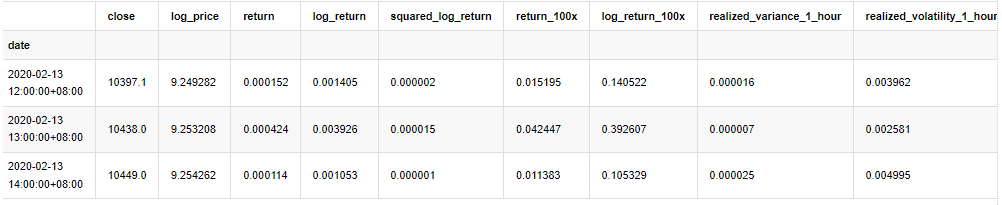

Sediakan data di luar sampel dengan cara yang sama

Dalam [5]:

# Prepare the data outside the sample with realized daily volatility
df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times
kline_1m['squared_log_return'] = np.power(kline_1m['log_return_100x'], 2)
kline_1m#.tail()
df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate daily logarithmic rate of return
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times
kline_test['squared_log_return'] = np.power(kline_test['log_return_100x'], 2)  # The exponential square of logarithmic daily rate of return
kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum()  # Resampling to days
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation
kline_test = kline_test[4:-2]

Untuk memahami data asas sampel, analisis deskriptif mudah dibuat seperti berikut:

Dalam [9]:

line_test = pd.DataFrame(kline_train['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'

mean = line_test.mean()  # Calculate mean value and standard deviation
std = line_test.std()

line_test.sort_values(by = 'log_return', inplace = True)  # Resort
s_r = line_test.reset_index(drop = False)  # After resorting, update index
s_r['p'] = (s_r.index - 0.5) / len(s_r)  # Calculate the percentile p(i)
s_r['q'] = (s_r['log_return'] - mean) / std  # Calculate the value of q

st = line_test.describe()
x1 ,y1 = 0.25, st['log_return']['25%']
x2 ,y2 = 0.75, st['log_return']['75%']

fig = plt.figure(figsize = (18,8))
layout = (2, 2)
ax1 = plt.subplot2grid(layout, (0, 0), colspan=2)# Plot the data distribution
ax2 = plt.subplot2grid(layout, (1, 0))# Plot histogram
ax3 = plt.subplot2grid(layout, (1, 1))# Draw the QQ chart, the straight line is the connection of the quarter digit, three-quarters digit, which is basically conforms to the normal distribution

ax1.scatter(line_test.index, line_test.values)
line_test.hist(bins=30,alpha = 0.5,ax = ax2)
line_test.plot(kind = 'kde', secondary_y=True,ax = ax2)
ax3.plot(s_r['p'],s_r['log_return'],'k.',alpha = 0.1)
ax3.plot([x1,x2],[y1,y2],'-r')
sns.despine()
plt.tight_layout()

Keluar[9]:

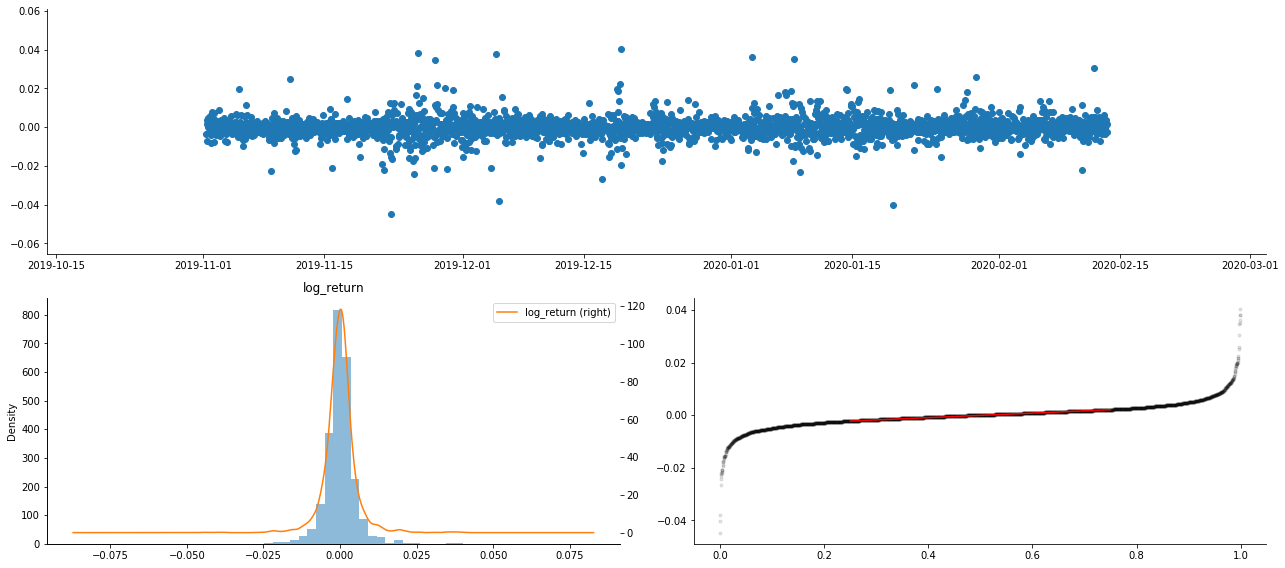
Akibatnya, terdapat pengumpulan turun naik dan kesan leverage yang jelas dalam carta siri masa pulangan logaritma.

Kebelakangan dalam carta pengedaran pulangan logaritma adalah kurang daripada 0, menunjukkan bahawa pulangan dalam sampel adalah sedikit negatif dan bias ke kanan.

Kebelakangan pengedaran data kurang daripada 1, menunjukkan bahawa pulangan dalam sampel sedikit positif dan sedikit bias kanan. Nilai kurtosis lebih besar daripada 3, menunjukkan bahawa hasil adalah ekor lemak tebal yang diedarkan.

Sekarang kita telah sampai ke titik ini, mari kita lakukan satu lagi ujian statistik. Dalam [7]:

line_test = pd.DataFrame(kline_all['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'
mean = line_test.mean()
std = line_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value',
                                    'Ks Test Value','Ks Test P-value',
                                    'Jarque Bera Test','Jarque Bera Test P-value'],
                    columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% line_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% line_test.kurt())
normal_result['model value']['Ks Test Value'] = stats.kstest(line_test, 'norm', (mean, std))[0]
normal_result['model value']['Ks Test P-value'] = stats.kstest(line_test, 'norm', (mean, std))[1]
normal_result['model value']['Jarque Bera Test'] = stats.jarque_bera(line_test)[0]
normal_result['model value']['Jarque Bera Test P-value'] = stats.jarque_bera(line_test)[1]
normal_result

Keluar[7]:

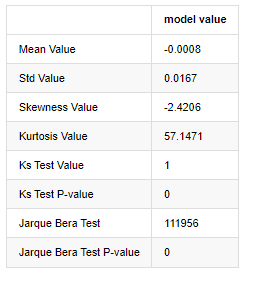
Statistik ujian Kolmogorov - Smirnov dan Jarque - Bera digunakan masing-masing. Hipotesis asal dicirikan oleh perbezaan yang signifikan dan pengedaran normal. Jika nilai P kurang daripada nilai kritikal tahap kepastian 0.05%, hipotesis asal ditolak.

Ia dapat dilihat bahawa nilai kurtosis lebih besar daripada 3, menunjukkan ciri-ciri ekor lemak tebal. Nilai P KS dan JB kurang daripada selang kepercayaan. Asumsi pengedaran normal ditolak, yang membuktikan bahawa kadar pulangan BTC tidak mempunyai ciri-ciri pengedaran normal, dan kajian empirikal mempunyai ciri-ciri ekor lemak tebal.

1-4. Perbandingan turun naik yang direalisasikan dan turun naik yang diperhatikan

Kami menggabungkan kuadrat_ log_ balik (logaritma hasil kuadrat) dan realized_varians (varians direalisasikan) untuk pemerhatian.

Dalam [11]:

fig, ax = plt.subplots(figsize=(18, 6))
start = '2020-03-08 00:00:00+08:00'
end = '2020-03-20 00:00:00+08:00'

np.abs(kline_all['squared_log_return']).loc[start:end].plot(ax=ax,label='squared log return')
kline_all['realized_variance_1_hour'].loc[start:end].plot(ax=ax,label='realized variance')
plt.legend(loc='best')

Keluar [11]:

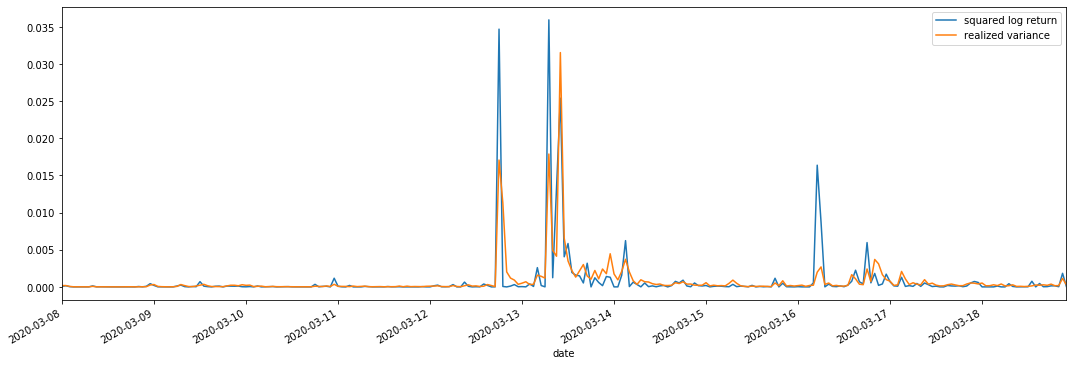
Ia dapat dilihat bahawa apabila julat varians yang direalisasikan lebih besar, turun naik julat kadar pulangan juga lebih besar, dan kadar pulangan yang direalisasikan lebih lancar.

Dari sudut pandangan teori semata-mata, RV lebih dekat dengan turun naik sebenar, sementara turun naik jangka pendek dihaluskan kerana turun naik intraday tergolong dalam data semalaman, jadi dari sudut pandangan pemerhatian, turun naik intraday lebih sesuai untuk frekuensi rendah pasaran saham turun naik. Perdagangan frekuensi tinggi dan ciri pasaran 7 * 24 jam BTC menjadikannya lebih sesuai untuk menggunakan RV untuk menentukan turun naik penanda aras.

2. Kelayakan siri masa

Jika ia adalah siri bukan stasioner, ia perlu diselaraskan kira-kira kepada siri stasioner. Cara biasa adalah dengan melakukan pemprosesan perbezaan. Secara teori, selepas banyak kali perbezaan, siri bukan stasioner boleh disampingkan kepada siri stasioner. Jika kovarian siri sampel stabil, jangkaan, varians dan kovarian pemerhatiannya tidak akan berubah dengan masa, menunjukkan bahawa siri sampel lebih mudah untuk kesimpulan dalam analisis statistik.

Ujian akar unit, iaitu ujian ADF, digunakan di sini. Ujian ADF menggunakan ujian t untuk mengamati signifikansi. Pada prinsipnya, jika siri tidak menunjukkan trend yang jelas, hanya item yang berterusan dipertahankan. Jika siri mempunyai trend, persamaan regresi harus merangkumi kedua-dua item yang berterusan dan item trend masa. Di samping itu, kriteria AIC dan BIC boleh digunakan untuk penilaian berdasarkan kriteria maklumat. Jika formula diperlukan, ia adalah seperti berikut: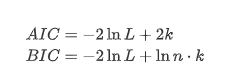

Dalam [8]:

stable_test = kline_all['log_return']
adftest = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='AIC')
adftest2 = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='BIC')
output=pd.DataFrame(index=['ADF Statistic Test Value', "ADF P-value", "Lags", "Number of Observations",
                           "Critical Value(1%)","Critical Value(5%)","Critical Value(10%)"],
                    columns=['AIC','BIC'])
output['AIC']['ADF Statistic Test Value'] = adftest[0]
output['AIC']['ADF P-value'] = adftest[1]
output['AIC']['Lags'] = adftest[2]
output['AIC']['Number of Observations'] = adftest[3]
output['AIC']['Critical Value(1%)'] = adftest[4]['1%']
output['AIC']['Critical Value(5%)'] = adftest[4]['5%']
output['AIC']['Critical Value(10%)'] = adftest[4]['10%']
output['BIC']['ADF Statistic Test Value'] = adftest2[0]
output['BIC']['ADF P-value'] = adftest2[1]
output['BIC']['Lags'] = adftest2[2]
output['BIC']['Number of Observations'] = adftest2[3]
output['BIC']['Critical Value(1%)'] = adftest2[4]['1%']
output['BIC']['Critical Value(5%)'] = adftest2[4]['5%']
output['BIC']['Critical Value(10%)'] = adftest2[4]['10%']
output

Keluar[8]: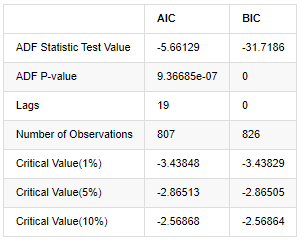

Asumsi asal adalah bahawa tidak ada akar unit dalam siri, iaitu, asumsi alternatif adalah bahawa siri ini tidak bergerak. nilai P ujian jauh kurang daripada 0.05% tahap keyakinan nilai penutupan, menolak andaian asal, jadi log kadar pulangan adalah siri yang tidak bergerak, boleh dimodelkan dengan menggunakan model siri masa statistik.

3. Pengenalan model dan penentuan pesanan

Untuk menubuhkan persamaan nilai purata, adalah perlu untuk melakukan ujian autocorrelation pada urutan untuk memastikan bahawa istilah ralat tidak mempunyai autocorrelation.

Dalam [19]:

tsplot(kline_all['log_return'], kline_all['log_return'], title='Log Return', lags=100)

Keluar[19]:

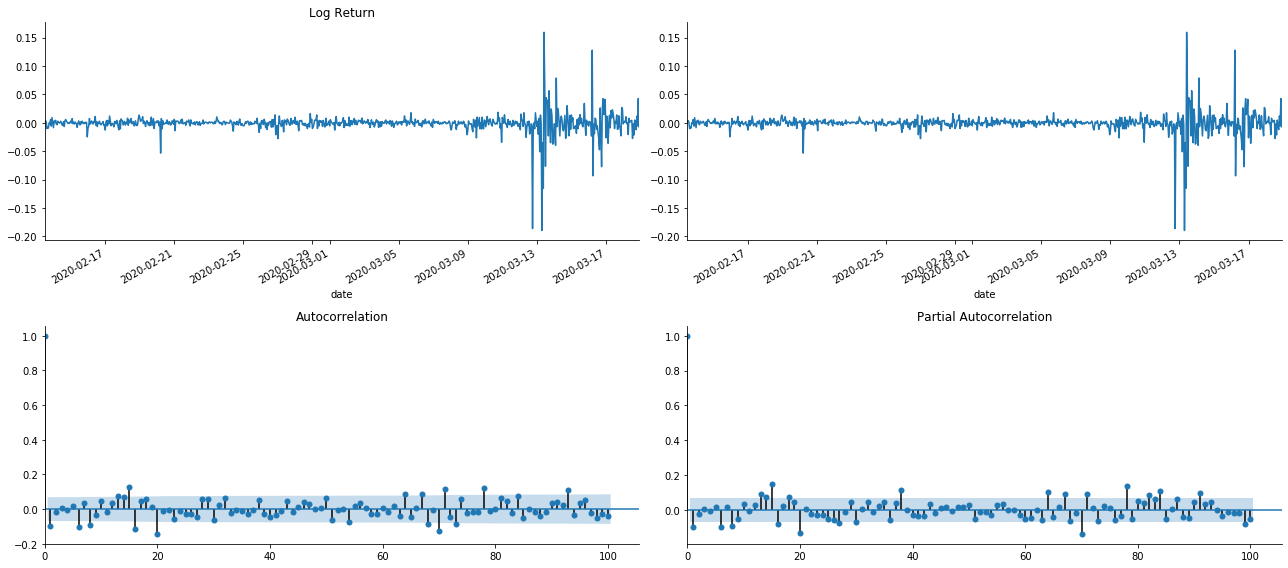
Kita boleh lihat bahawa kesan pemotongan adalah sempurna. Pada masa itu, gambar ini memberi saya inspirasi. Adakah pasaran benar-benar tidak sah? Untuk mengesahkan, kita akan melakukan analisis autocorrelation pada siri kembalinya dan menentukan urutan lag model.

Gabungan korelasi yang biasa digunakan adalah untuk mengukur korelasi antara ia dan dirinya sendiri, iaitu korelasi antara r ((t) dan r (t-l) pada masa tertentu di masa lalu: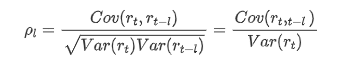

Kemudian mari kita lakukan ujian kuantitatif. Asumsi asal adalah bahawa semua pekali autocorrelation adalah 0, iaitu, tidak ada autocorrelation dalam siri. Rumus statistik ujian ditulis seperti berikut: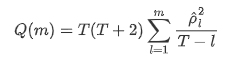

Sepuluh pekali autocorrelation diambil untuk analisis, seperti berikut:

Dalam [9]:

acf,q,p = sm.tsa.acf(kline_all['log_return'], nlags=15,unbiased=True,qstat = True, fft=False)  # Test 10 autocorrelation coefficients
output = pd.DataFrame(np.c_[range(1,16), acf[1:], q, p], columns=['lag', 'ACF', 'Q', 'P-value'])
output = output.set_index('lag')
output

Keluar[9]: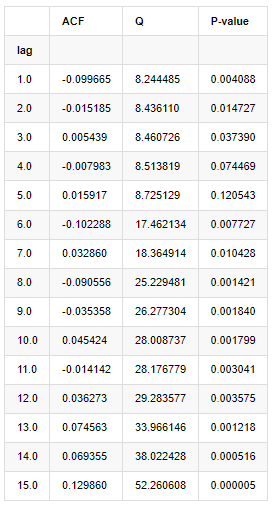

Menurut statistik ujian Q dan nilai P, kita dapat melihat bahawa fungsi auto-korrelasi ACF secara beransur-ansur menjadi 0 selepas urutan 0. Nilai-nilai P statistik ujian Q cukup kecil untuk menolak andaian asal, jadi terdapat auto-korrelasi dalam siri.

4. Model ARMA

Model AR dan MA agak mudah. Secara ringkasnya, Markdown terlalu letih untuk menulis formula. Jika anda berminat, sila periksa sendiri. Model AR (Autoregression) terutamanya digunakan untuk memodelkan siri masa. Jika siri telah lulus ujian ACF, iaitu, pekali auto-korrelasi dengan selang 1 adalah penting, iaitu, data pada masa mungkin berguna untuk meramalkan masa t.

Model MA (Melayu Purata) menggunakan gangguan rawak atau ramalan ralat dari tempoh q yang lalu untuk menyatakan nilai ramalan semasa secara linear.

Untuk menerangkan sepenuhnya struktur dinamik data, adalah perlu untuk meningkatkan urutan model AR atau MA, tetapi parameter sedemikian akan membuat pengiraan lebih rumit. oleh itu, untuk mempermudah proses ini, model purata bergerak autoregressif (ARMA) dicadangkan.

Oleh kerana siri masa harga umumnya tidak tetap, dan kesan pengoptimuman kaedah perbezaan pada stasionari telah dibincangkan sebelumnya, model ARIMA (p, d, q) (jumlah purata bergerak autoregressif) menambah pemprosesan perbezaan d-order berdasarkan penerapan model sedia ada kepada siri.

Secara ringkasnya, satu-satunya perbezaan antara model ARIMA dan proses pembinaan model ARMA adalah bahawa jika hasil yang tidak stabil diperoleh selepas menganalisis stabilitas, model akan membuat perbezaan kuadrat kepada siri secara langsung dan kemudian melakukan ujian stabilitas, dan kemudian menentukan urutan p dan q sehingga siri stabil. Selepas membina model dan mengevaluasinya, ramalan berikutnya akan dibuat, menghapuskan langkah kembali untuk melakukan perbezaan. Walau bagaimanapun, perbezaan harga urutan kedua tidak bermakna, jadi ARMA adalah pilihan terbaik.

Pemilihan pesanan

Seterusnya, kita boleh memilih urutan secara langsung oleh kriteria maklumat, di sini kita cuba dengan diagram termodinamik AIC dan BIC.

Dalam [10]:

def select_best_params():
    ps = range(0, 4)
    ds= range(1, 2)
    qs = range(0, 4)
    parameters = product(ps, ds, qs)
    parameters_list = list(parameters)

    p_min = 0
    d_min = 0
    q_min = 0
    p_max = 3
    d_max = 3
    q_max = 3

    results_aic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    results_bic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    
    best_params = []
    aic_results = []
    bic_results = []
    hqic_results = []
    best_aic = float("inf")
    best_bic = float("inf")
    best_hqic = float("inf")
    warnings.filterwarnings('ignore')
    for param in parameters_list:
        try:
            model = sm.tsa.SARIMAX(kline_all['log_price'], order=(param[0], param[1], param[2])).fit(disp=-1)
            results_aic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.aic
            results_bic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.bic
        except ValueError:
            continue    
           
        aic_results.append([param, model.aic])
        bic_results.append([param, model.bic])
        hqic_results.append([param, model.hqic])
    
    results_aic = results_aic[results_aic.columns].astype(float)
    results_bic = results_bic[results_bic.columns].astype(float)
    
    # Draw thermodynamic diagrams of AIC and BIC to find the best
    fig = plt.figure(figsize=(18, 9))
    layout = (2, 2)
    aic_ax = plt.subplot2grid(layout, (0, 0))
    bic_ax = plt.subplot2grid(layout, (0, 1))

    aic_ax = sns.heatmap(results_aic,mask=results_aic.isnull(),ax=aic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    aic_ax.set_title('AIC');
    bic_ax = sns.heatmap(results_bic,mask=results_bic.isnull(),ax=bic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    bic_ax.set_title('BIC');
    
    aic_df = pd.DataFrame(aic_results)
    aic_df.columns = ['params', 'aic']   
    best_params.append(aic_df.params[aic_df.aic.idxmin()])
    print('AIC best param: {}'.format(aic_df.params[aic_df.aic.idxmin()]))
    
    bic_df = pd.DataFrame(bic_results)
    bic_df.columns = ['params', 'bic']
    best_params.append(bic_df.params[bic_df.bic.idxmin()])
    print('BIC best param: {}'.format(bic_df.params[bic_df.bic.idxmin()]))
    
    hqic_df = pd.DataFrame(hqic_results)
    hqic_df.columns = ['params', 'hqic']
    best_params.append(hqic_df.params[hqic_df.hqic.idxmin()])
    print('HQIC best param: {}'.format(hqic_df.params[hqic_df.hqic.idxmin()]))

    for best_param in best_params:
        if best_params.count(best_param)>=2:
            print('Best Param Selected: {}'.format(best_param))
            return best_param 

best_param = select_best_params()

Keluar[10]: Param AIC terbaik: (0, 1, 1) Param terbaik BIC: (0, 1, 1) Param terbaik HQIC: (0, 1, 1) Param Terbaik Dipilih: (0, 1, 1)

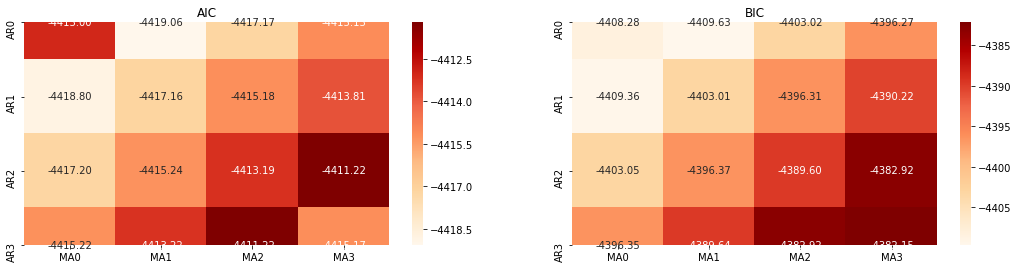
Adalah jelas bahawa kombinasi parameter peringkat pertama yang optimum untuk harga logaritma adalah (0,1,1), yang mudah dan mudah. log_return (tingkat pulangan logaritma) melakukan operasi yang sama. Nilai optimum AIC adalah (4,3), dan nilai optimum BIC adalah (0,1). Jadi kombinasi parameter optimum untuk log_return (tingkat pulangan logaritma) adalah (0,1).

4-2. pemodelan dan pencocokan ARMA

Koefisien suku tidak diperlukan, tetapi SARIMAX lebih kaya dengan atribut, jadi diputuskan untuk memilih model ini untuk pemodelan dan secara kebetulan membuat analisis deskriptif seperti berikut:

Dalam [11]:

params = (0, 0, 1)
training_model = smt.SARIMAX(endog=kline_all['log_return'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
model_results = training_model.fit(disp=False)
model_results.summary()

Keluar [11]: Hasil Model Ruang Negeri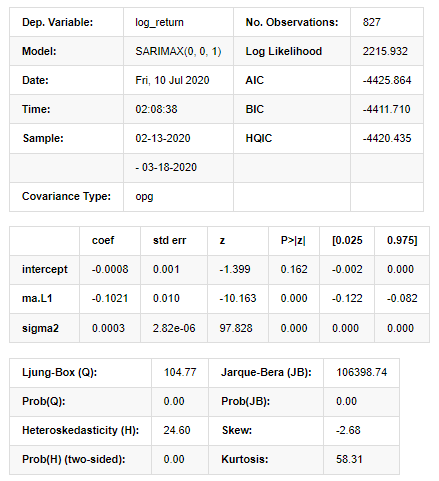

Amaran: [1] Matriks kovarians dikira menggunakan hasil luar gradien (langkah kompleks). Dalam [27]:

model_results.plot_diagnostics(figsize=(18, 10));

Keluar[27]:

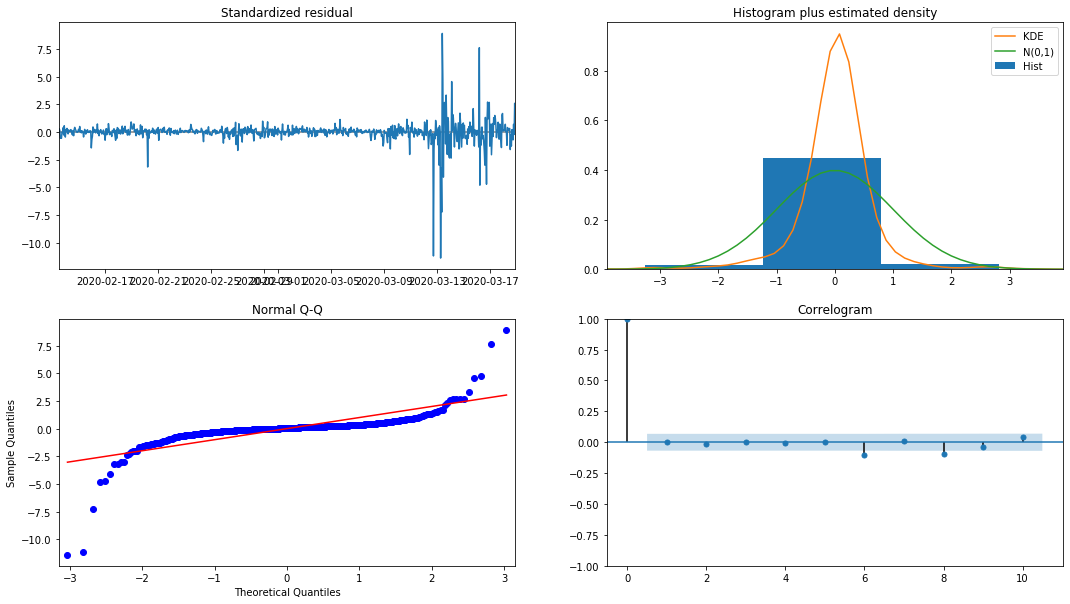
Ketumpatan kebarangkalian KDE dalam histogram jauh dari pengagihan normal N (0,1), menunjukkan bahawa residual bukan pengagihan normal. Dalam plot kuantil QQ, residual sampel yang diambil daripada pengagihan normal standard tidak sepenuhnya mengikuti trend linear, jadi ia disahkan lagi bahawa residual bukan pengagihan normal dan lebih dekat dengan bunyi bising putih.

Kemudian, setelah mengatakan itu, sama ada model itu boleh digunakan masih perlu diuji.

Ujian model

Kesan pencocokan residual tidak ideal, jadi kami melakukan ujian Durbin Watson di atasnya. Hipotesis asal ujian adalah bahawa urutan tidak mempunyai autocorrelation, dan urutan hipotesis alternatif tidak bergerak. Di samping itu, jika nilai P ujian LB, JB dan H kurang daripada nilai kritikal tahap kepastian 0.05%, hipotesis asal akan ditolak.

Dalam [12]:

het_method='breakvar'
norm_method='jarquebera'
sercor_method='ljungbox'

(het_stat, het_p) = model_results.test_heteroskedasticity(het_method)[0]
norm_stat, norm_p, skew, kurtosis = model_results.test_normality(norm_method)[0]

sercor_stat, sercor_p = model_results.test_serial_correlation(method=sercor_method)[0]
sercor_stat = sercor_stat[-1] # The last value of the maximum period
sercor_p = sercor_p[-1]

dw = sm.stats.stattools.durbin_watson(model_results.filter_results.standardized_forecasts_error[0, model_results.loglikelihood_burn:])

arroots_outside_unit_circle = np.all(np.abs(model_results.arroots) > 1)
maroots_outside_unit_circle = np.all(np.abs(model_results.maroots) > 1)

print('Test heteroskedasticity of residuals ({}): stat={:.3f}, p={:.3f}'.format(het_method, het_stat, het_p));
print('\nTest normality of residuals ({}): stat={:.3f}, p={:.3f}'.format(norm_method, norm_stat, norm_p));
print('\nTest serial correlation of residuals ({}): stat={:.3f}, p={:.3f}'.format(sercor_method, sercor_stat, sercor_p));
print('\nDurbin-Watson test on residuals: d={:.2f}\n\t(NB: 2 means no serial correlation, 0=pos, 4=neg)'.format(dw))
print('\nTest for all AR roots outside unit circle (>1): {}'.format(arroots_outside_unit_circle))
print('\nTest for all MA roots outside unit circle (>1): {}'.format(maroots_outside_unit_circle))

root_test=pd.DataFrame(index=['Durbin-Watson test on residuals','Test for all AR roots outside unit circle (>1)','Test for all MA roots outside unit circle (>1)'],columns=['c'])
root_test['c']['Durbin-Watson test on residuals']=dw
root_test['c']['Test for all AR roots outside unit circle (>1)']=arroots_outside_unit_circle
root_test['c']['Test for all MA roots outside unit circle (>1)']=maroots_outside_unit_circle
root_test

Keluar[12]: Ujian heteroskedastikiti sisa (breakvar): stat=24.598, p=0.000

Normaliti ujian baki (jarquebera): stat=106398.739, p=0.000

Penyelarasan siri ujian baki (ljungbox): stat=104.767, p=0.000

Ujian Durbin-Watson untuk sisa: d=2.00 (NB: 2 bermaksud tiada korelasi siri, 0=pos, 4=negatif)

Ujian untuk semua akar AR di luar bulatan unit (>1): Betul

Ujian untuk semua akar MA di luar bulatan unit (>1): Betul

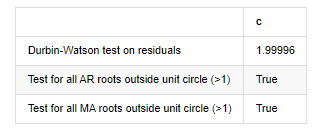
Dalam [13]:

kline_all['log_price_dif1'] = kline_all['log_price'].diff(1)
kline_all = kline_all[1:]
kline_train = kline_all

training_label = 'log_return'
training_ts = pd.DataFrame(kline_train[training_label], dtype=np.float)

delta = model_results.fittedvalues - training_ts[training_label]
adjR = 1 - delta.var()/training_ts[training_label].var()
adjR_test=pd.DataFrame(index=['adjR2'],columns=['Value'])
adjR_test['Value']['adjR2']=adjR**2
adjR_test

Keluar[13]:

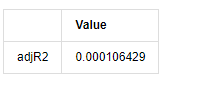
Jika statistik ujian Durbin Watson adalah sama dengan 2, mengesahkan bahawa siri tidak mempunyai korelasi, dan nilai statistiknya diedarkan antara (0,4). Berhampiran dengan 0 bermakna korelasi positif tinggi, sementara berhampiran dengan 4 bermaksud korelasi negatif tinggi. Di sini ia kira-kira sama dengan 2. Nilai P ujian lain cukup kecil, akar ciri unit berada di luar bulatan unit, dan semakin besar nilai adjR2 yang diubah suai, semakin baik ia akan menjadi.

Dalam [14]:

model_results.params

Keluar[14]: Mencegat -0.000817 ma.L1 -0.102102 sigma2 0.000275 djenis: float64

Untuk meringkaskan, parameter penetapan pesanan ini pada dasarnya dapat memenuhi keperluan pemodelan siri masa dan pemodelan turun naik berikutnya, tetapi kesan pencocokan adalah seperti ini.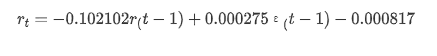

4-4. ramalan model

Seterusnya, model terlatih disamakan ke hadapan. statsmodels menyediakan pilihan statik dan dinamik untuk pencocokan dan ramalan. Perbezaannya terletak pada sama ada nilai pemerhatian digunakan dalam langkah ramalan seterusnya, atau nilai ramalan yang dihasilkan dalam langkah sebelumnya digunakan secara berulang. Kesan ramalan log_return (peratusan logaritma pulangan) adalah seperti berikut:

Dalam [37]:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=False)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Keluar[37]:

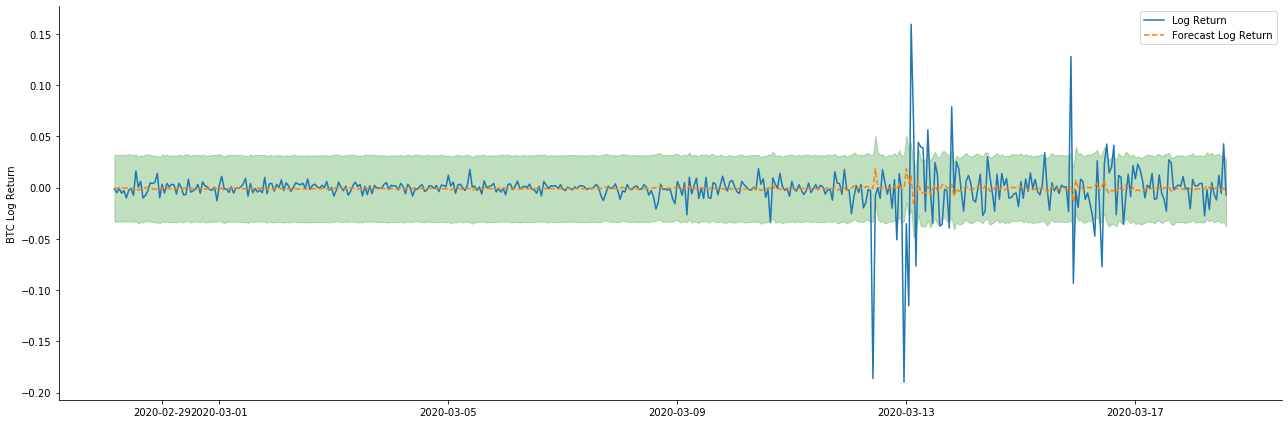
Ia dapat dilihat bahawa kesan pemasangan mod statik pada sampel sangat baik, data sampel boleh hampir dilindungi oleh selang keyakinan 95%, dan mod dinamik agak tidak terkawal.

Jadi mari kita lihat kesan pencocokan data dalam mod dinamik:

Dalam [38]:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=True)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Keluar[38]:

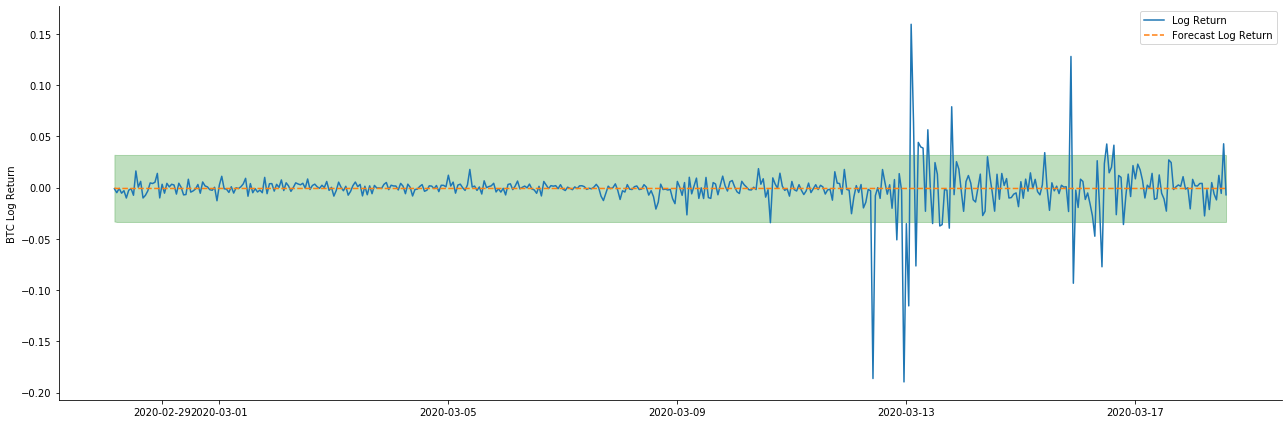
Ia dapat dilihat bahawa kesan pemasangan kedua-dua model pada sampel adalah sangat baik, dan nilai purata boleh hampir dilindungi oleh selang keyakinan 95%, tetapi model statik jelas lebih sesuai.

Dalam [41]:

# Out-of-sample predicted data predict()
start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-20 23:00:00+08:00'
model = False

predict_step = 50
predicts_ARIMA_normal = model_results.get_prediction(start=start_date, dynamic=model, full_reports=True)
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:]

predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=model)
ci_normal_out = predicts_ARIMA_normal_out.conf_int().loc[start_date:end_date]

fig, ax = plt.subplots(figsize=(18,8))
kline_test.loc[start_date:end_date, 'log_return'].plot(ax=ax, label='Benchmark Log Return')

predicts_ARIMA_normal.predicted_mean.plot(ax=ax, style='g', label='In Sample Forecast')
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='g', alpha=0.1)

predicts_ARIMA_normal_out.predicted_mean.loc[:end_date].plot(ax=ax, style='r--', label='Out of Sample Forecast')
ax.fill_between(ci_normal_out.index, ci_normal_out.iloc[:,0], ci_normal_out.iloc[:,1], color='r', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

Keluar[41]:

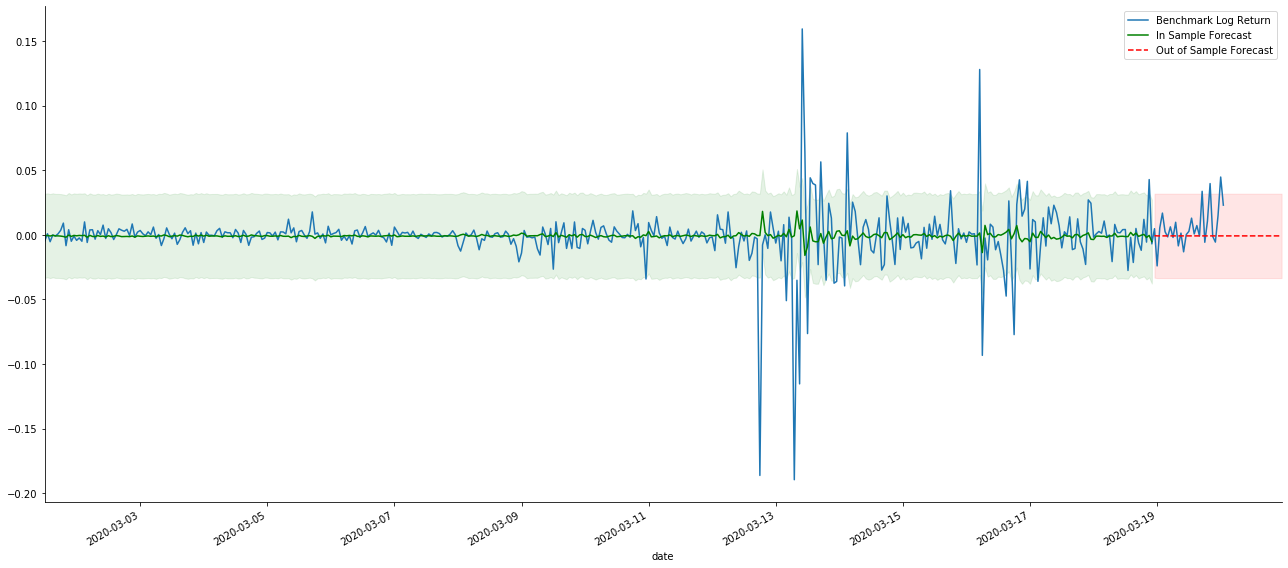
Oleh kerana pencocokan data dalam sampel adalah ramalan maju, apabila jumlah maklumat dalam sampel mencukupi, model statik cenderung untuk pencocokan yang berlebihan, sementara model dinamik tidak mempunyai pembolehubah bergantung yang boleh dipercayai, dan kesannya menjadi semakin buruk selepas pengulangan.

Jika kita membalikkan ramalan kadar pulangan kepada log_price (harga logaritma), perlawanan ditunjukkan dalam gambar di bawah:

Dalam [42]:

params = (0, 1, 1)
mod = smt.SARIMAX(endog=kline_all['log_price'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
res = mod.fit(disp=False)

start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-15 23:00:00+08:00'

predicts_ARIMA_normal = res.get_prediction(start=start_date, dynamic=False, full_results=False)
predicts_ARIMA_dynamic = res.get_prediction(start=start_date, dynamic=True, full_results=False)

fig, ax = plt.subplots(figsize=(18,6))
kline_test.loc[start_date:end_date, 'log_price'].plot(ax=ax, label='Log Price')

predicts_ARIMA_normal.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='r--', label='Normal Prediction')
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:end_date]
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='r', alpha=0.1)

predicts_ARIMA_dynamic.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='g', label='Dynamic Prediction')
ci_dynamic = predicts_ARIMA_dynamic.conf_int().loc[start_date:end_date]
ax.fill_between(ci_dynamic.index, ci_dynamic.iloc[:,0], ci_dynamic.iloc[:,1], color='g', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

Keluar[42]:

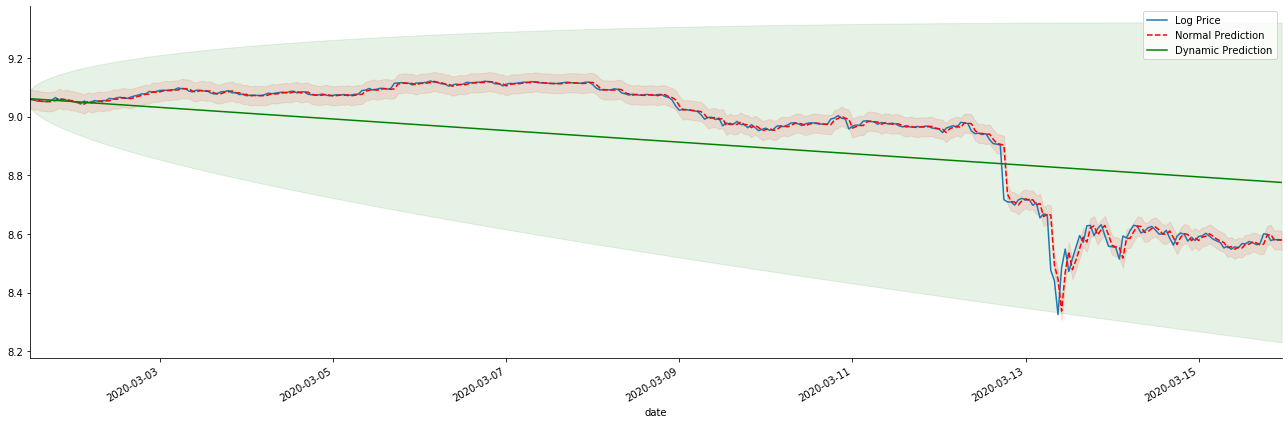
Ia adalah mudah untuk melihat kelebihan yang sepadan model statik dan perbezaan yang melampau antara model dinamik dan model statik dalam ramalan jangka panjang. garis bertitik merah dan julat merah jambu... anda tidak boleh mengatakan bahawa ramalan model ini adalah salah. selepas semua, ia meliputi trend purata bergerak sepenuhnya, tetapi... adakah ia bermakna?

Pada hakikatnya, model ARMA itu sendiri tidak salah, kerana masalahnya bukan model itu sendiri, tetapi logik objektif perkara itu sendiri. Model siri masa hanya boleh ditubuhkan berdasarkan korelasi antara pemerhatian sebelumnya dan berikutnya. Oleh itu, mustahil untuk memodelkan siri bunyi putih. Oleh itu, semua kerja sebelumnya berdasarkan anggapan berani bahawa siri kadar pulangan BTC tidak boleh bebas dan diedarkan secara sama.

Secara umum, siri kadar pulangan adalah siri perbezaan martingale, yang bermaksud bahawa kadar pulangan tidak dapat diramalkan, dan andaian kecekapan yang lemah pasaran yang sepadan berlaku.

Walau bagaimanapun, urutan baki yang sepadan juga merupakan urutan perbezaan martingale. Urutan perbezaan martingale mungkin tidak bebas dan diedarkan secara sama, tetapi varians bersyarat mungkin bergantung pada nilai masa lalu, jadi auto-korrelasi orde pertama hilang, tetapi masih ada auto-korrelasi orde yang lebih tinggi, yang juga merupakan prasyarat penting untuk volatiliti dimodelkan dan diamati.

Jika logik seperti itu berlaku, maka premis membina pelbagai model turun naik juga berlaku. jadi untuk siri kadar pulangan, jika pasaran yang kurang cekap berpuas hati, maka nilai purata mesti sukar untuk diramalkan, tetapi variansnya boleh diramalkan. dan ARMA yang sepadan memberikan penanda aras siri masa yang berkualiti adil, maka kualiti juga menentukan kualiti ramalan turun naik.

Akhirnya, mari kita menilai kesan ramalan dengan mudah. Dengan kesilapan sebagai penanda aras penilaian, penunjuk di dalam dan di luar sampel adalah seperti berikut:

Dalam [15]:

start = '2020-02-14 00:00:00+08:00'
predicts_ARIMA_normal = model_results.get_prediction(dynamic=False)
predicts_ARIMA_dynamic = model_results.get_prediction(dynamic=True)
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [rmse(predicts_ARIMA_normal.predicted_mean[1:], kline_test[training_label][:826]),
                          rmse(predicts_ARIMA_dynamic.predicted_mean[1:], kline_test[training_label][:826])]
compare_ARCH_X['MAPE'] = [mape(predicts_ARIMA_normal.predicted_mean[:50], kline_test[training_label][:50]),
                          mape(predicts_ARIMA_dynamic.predicted_mean[:50], kline_test[training_label][:50])]
compare_ARCH_X

Keluar[15]: Kesilapan Akar Rendah Kuadrat (RMSE): 0.0184 Kesilapan Akar Rata-rata Kuadrat (RMSE): 0.0167 Kesilapan Peratusan Absolut Purata (MAPE): 2.25e+03 Kesilapan Peratusan Absolut Purata (MAPE): 395

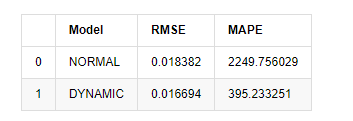
Ia boleh dilihat bahawa model statik sedikit lebih baik daripada model dinamik dari segi kesamaan ralat antara nilai yang diramalkan dan nilai sebenar. Ia sepadan dengan kadar pulangan logaritma Bitcoin dengan baik, yang pada dasarnya sejajar dengan jangkaan. Ramalan dinamik tidak mempunyai maklumat pembolehubah yang lebih tepat, dan ralat juga diperbesar oleh pengulangan, jadi kesan ramalan adalah miskin. MAPE lebih besar daripada 100%, jadi kualiti pencocokan sebenar kedua-dua model tidak ideal.

Dalam [18]:

predict_step = 50
predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=False)
predicts_ARIMA_dynamic_out = model_results.get_forecast(steps=predict_step, dynamic=True)
testing_ts = kline_test
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [get_rmse(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_rmse(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X['MAPE'] = [get_mape(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_mape(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X

Keluar [1]:

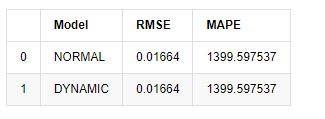
Oleh kerana ramalan seterusnya di luar sampel bergantung pada hasil langkah sebelumnya, hanya model dinamik yang berkesan. Walau bagaimanapun, kecacatan ralat jangka panjang model dinamik membawa kepada keupayaan ramalan keseluruhan yang tidak mencukupi, jadi langkah seterusnya diramalkan paling banyak.

Untuk meringkaskan, model statik model ARMA sesuai untuk mencocokkan kadar pulangan intra sampel Bitcoin. Ramalan jangka pendek kadar pulangan boleh merangkumi selang keyakinan dengan berkesan, tetapi ramalan jangka panjang sangat sukar, yang memenuhi keberkesanan pasaran yang lemah. Selepas ujian, kadar pulangan dalam selang sampel memenuhi premis pemerhatian turun naik berikutnya.

5. Kesan ARCH

Kesan model ARCH adalah korelasi siri urutan heteroskedastikiti bersyarat. Ujian campuran Ljung Box digunakan untuk menguji korelasi siri persegi sisa untuk menentukan sama ada terdapat kesan ARCH. Jika ujian kesan ARCH diluluskan, iaitu siri itu mempunyai heteroskedastikiti, langkah seterusnya pemodelan GARCH dapat dilakukan untuk menganggarkan persamaan purata dan persamaan volatiliti bersama-sama. Jika tidak, model perlu dioptimumkan dan disesuaikan semula, seperti pemprosesan pembezaan atau siri timbal balik.

Kami menyediakan beberapa set data dan pembolehubah global di sini:

Dalam [33]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=count_num, start=start_date)  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=count_num, start=start_date)  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate the daily logarithmic rate of return
kline_test['return'] = kline_test['log_price'].pct_change().dropna()
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate the logarithmic rate of return
kline_test['squared_log_return'] = np.power(kline_test['log_return'], 2)  # Exponential square of log daily return rate

kline_test['return_100x'] = np.multiply(kline_test['return'], 100)
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times

kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy() # Resampling to days 
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation

kline_test = kline_test[4:-2500]
kline_test.head(3)

Keluar[33]:

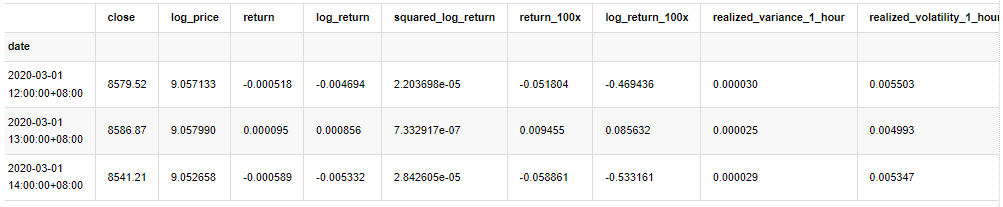
Dalam [22]:

cc = 3
model_p = 1
predict_lag = 30
label = 'log_return'

training_label = label
training_ts = pd.DataFrame(kline_test[training_label], dtype=np.float)

training_arch_label = label
training_arch = pd.DataFrame(kline_test[training_arch_label], dtype=np.float)

training_garch_label = label
training_garch = pd.DataFrame(kline_test[training_garch_label], dtype=np.float)

training_egarch_label = label
training_egarch = pd.DataFrame(kline_test[training_egarch_label], dtype=np.float)

training_arch.plot(figsize = (18,4))

Keluar[22]: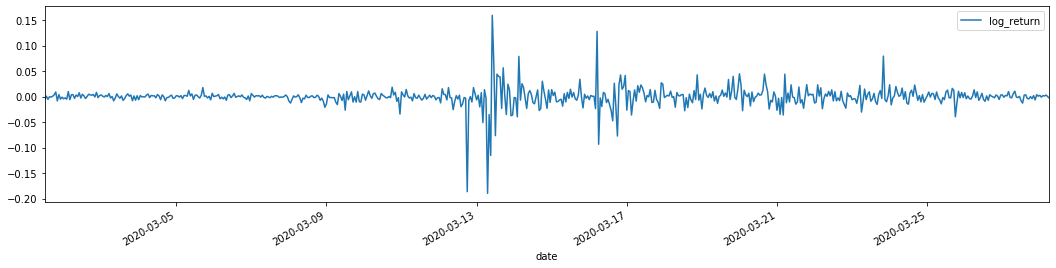

Kadar pulangan logaritma ditunjukkan di atas. Seterusnya, kita perlu menguji kesan ARCH sampel. Kami menubuhkan siri baki dalam sampel berdasarkan ARMA. Beberapa siri dan siri persegi baki dan baki dikira terlebih dahulu:

Dalam [20]:

training_arma_model = smt.SARIMAX(endog=training_ts, trend='c', order=(0, 0, 1), seasonal_order=(0, 0, 0, 0))
arma_model_results = training_arma_model.fit(disp=False)
arma_model_results.summary()
training_arma_fitvalue = pd.DataFrame(arma_model_results.fittedvalues,dtype=np.float)
at = pd.merge(training_ts, training_arma_fitvalue, on='date')
at.columns = ['log_return', 'model_fit']
at['res'] = at['log_return'] - at['model_fit']
at['res2'] = np.square(at['res'])
at.head()

Keluar[20]:

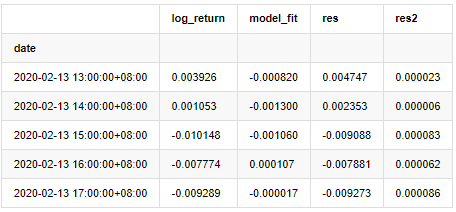
Siri baki sampel kemudiannya dicatatkan

Dalam [69]:

fig, ax = plt.subplots(figsize=(18, 6))
ax1 = fig.add_subplot(2,1,1)
at['res'][1:].plot(ax=ax1,label='resid')
plt.legend(loc='best')

ax2 = fig.add_subplot(2,1,2)
at['res2'][1:].plot(ax=ax2,label='resid2')

plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Keluar[69]:

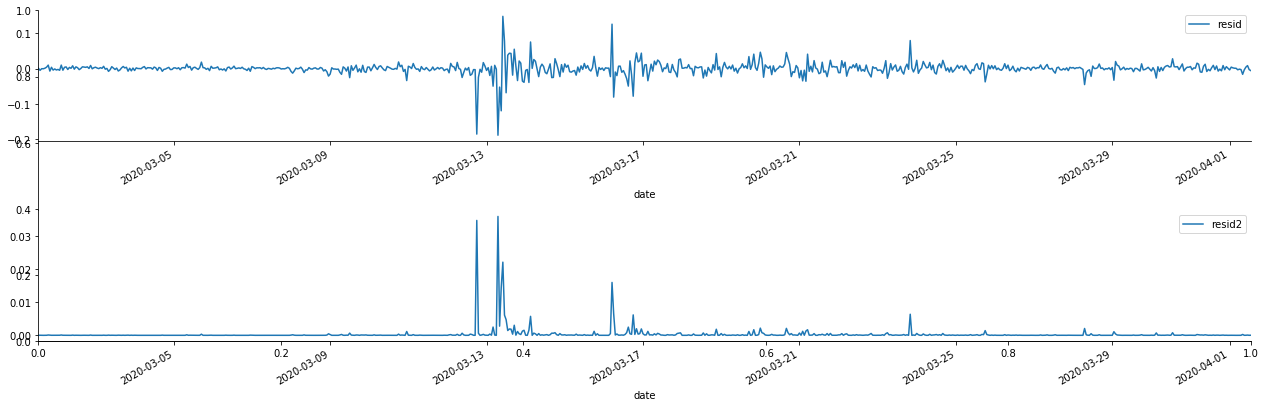
Ia dapat dilihat bahawa siri residu mempunyai ciri pengumpulan yang jelas, dan ia boleh dinilai pada mulanya bahawa siri mempunyai kesan ARCH. ACF juga diambil untuk menguji autocorrelation residu kuadrat, dan hasilnya adalah seperti berikut.

Dalam [70]:

figure = plt.figure(figsize=(18,4))
ax1 = figure.add_subplot(111)
fig = sm.graphics.tsa.plot_acf(at['res2'],lags = 40, ax=ax1)

Keluar[70]:

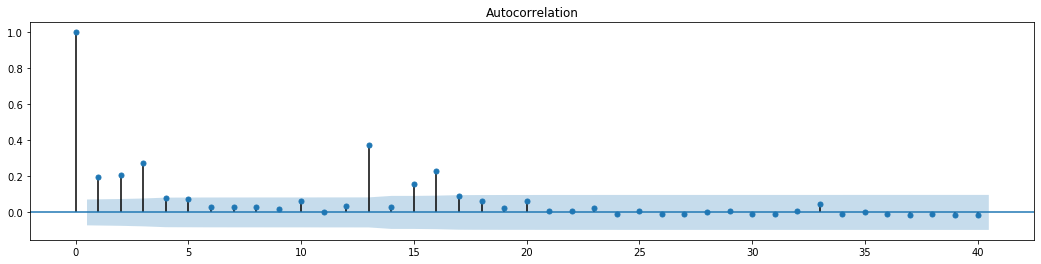
Asumsi asal untuk ujian pencampuran siri adalah bahawa siri tidak mempunyai korelasi. Ia dapat dilihat bahawa nilai P yang sepadan dari 20 perintah data pertama adalah kurang daripada nilai kritikal tahap kepastian 0.05%. Oleh itu, anggapan asal ditolak, iaitu residu siri mempunyai kesan ARCH. Model varians boleh ditubuhkan melalui model jenis ARCH untuk menyesuaikan heteroscedasticity siri residu dan lebih lanjut meramalkan volatiliti.

6. pemodelan GARCH

Sebelum melakukan pemodelan GARCH, kita perlu berurusan dengan bahagian ekor lemak siri. Kerana istilah ralat siri dalam hipotesis perlu mematuhi pengedaran normal atau pengedaran t, dan kita telah sebelum ini disahkan bahawa siri hasil mempunyai pengedaran ekor lemak, jadi kita perlu menerangkan dan menambah bahagian ini.

Dalam pemodelan GARCH, item ralat menyediakan pilihan pengedaran normal, pengedaran t, pengedaran GED (pengedaran ralat umum) dan pengedaran t Pelajar Skewed.

Berkaitan

Lebih lanjut